|
ИНФОРМАЦИОННЫЕ МЕРЫ И ИХ ИСПОЛЬЗОВАНИЕ В СОЦИОЛОГИЧЕСКОМ АНАЛИЗЕ
В дальнейшем изложении под объектом будет пониматься заполненная анкета, состоящая из ответов на вопросы. Множество таких анкет будет именоваться множеством объектов α. Набор вопросов для всех объектов обозначается как множество признаков F. Так как на один вопрос можно дать несколько ответов, то длю каждого признака 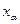 существует множество градаций существует множество градаций 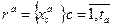 , где , где  - количество градаций признака - количество градаций признака  , равное количеству логических возможностей на вопрос, соответствующий признаку , равное количеству логических возможностей на вопрос, соответствующий признаку  . Вероятность того, что объект по признаку . Вероятность того, что объект по признаку  попадает в градацию попадает в градацию  будем обозначать как будем обозначать как  Очевидно, набор совместных вероятностей признаков Очевидно, набор совместных вероятностей признаков 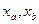 будет будет  где где 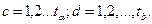 Информация признака Информация признака 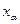 о признаке о признаке  дается формулой. дается формулой.
 (1) (1)
где  ) и ) и  - энтропии признаков - энтропии признаков  и и  ; ;  - их совместная энтропия. Свойства этих величин описаны К. Шенноном [1]. - их совместная энтропия. Свойства этих величин описаны К. Шенноном [1].
Эквивалентным признаком  для данного множества признаков для данного множества признаков  имеющих множество градаций имеющих множество градаций  назовем признак, множество градаций которого равно декартовому произведению множеств градаций каждого из признаков назовем признак, множество градаций которого равно декартовому произведению множеств градаций каждого из признаков 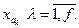
Множество градаций эквивалентного признака  обозначим как обозначим как  . Очевидно, что . Очевидно, что  . Условимся, что разбиение множества объектов на подмножества по признаку . Условимся, что разбиение множества объектов на подмножества по признаку  порождает множество подмножеств объектов порождает множество подмножеств объектов 
Процедура образования эквивалентного признака соответствует замене комплекса вопросов в анкете на один сложный вопрос.
Введение эквивалентного признака удобно в тех случаях, когда, например, изучается связь между комплексами признаков. Тогда можно заменить рассмотрение связи между комплексами признаков на рассмотрение связи между эквивалентными признаками, представляющими эти комплексы признаков.
За меру различия между подмножествами объектов  и и  по признаку по признаку  принимается «разностное информационное отношение» принимается «разностное информационное отношение»
 (2) (2)
Здесь  - потеря информации признака - потеря информации признака  о признаке о признаке  при объединении градаций при объединении градаций  и и 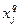 в признаке в признаке  . .
 (3) (3)

где штрихованные величины вычисляются после объединения градаций, а не штрихованные – до объединения.
Докажем несколько свойств:
1. 
Правая часть этого неравенства следует из (3). Докажем левую часть неравенства. Для этого достаточно показать, что
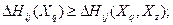 (4) (4)

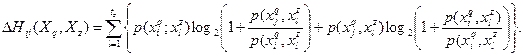 (5) (5)
Покажем, что

К последнему выражению применимо неравенство Иенсена из теории выпуклых функций [2], так как  и функция и функция  выпукла вверх. выпукла вверх.

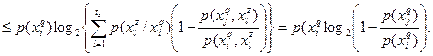
2. Если множества объектов  и и  максимально различны по признаку максимально различны по признаку  , то , то 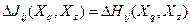 и и  . .
Определение 1. Множества объектов  и и  называются максимально различными по признаку называются максимально различными по признаку  , если , если  – пустое множество. – пустое множество.
Очевидно, что в этом случае в  не будет ни одного объекта одинакового по не будет ни одного объекта одинакового по  с каким-либо другим объектом из с каким-либо другим объектом из 
Определение 2. Множества  и и  называются одинаковыми по признаку называются одинаковыми по признаку  , если , если

Учитывая сказанное, нетрудно получить, что 
Пусть  и и  Введем Введем 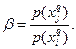 Тогда Тогда  будет иметь вид будет иметь вид 
График функции дан на рис. 1.

Если множества  и и  максимально различны по признаку максимально различны по признаку  , то потеря информации о признаке при объединении , то потеря информации о признаке при объединении  и и  будет тем меньше, чем больше отношение количества объектов в будет тем меньше, чем больше отношение количества объектов в  и и  . .
Из свойства 1 следует, что в общем случае значения  лежат в заштрихованной области (см. рис. 1). лежат в заштрихованной области (см. рис. 1).
3. Если  и и  одинаковы по признаку одинаковы по признаку  , то , то  . Это легко доказывается, если использовать определение (2). Очевидно также, что в этом случае . Это легко доказывается, если использовать определение (2). Очевидно также, что в этом случае  . .
4. Если  , то , то  и и  одинаковы по признаку одинаковы по признаку  . Введем обозначения . Введем обозначения  и и 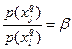 . В них . В них  запишется в виде запишется в виде
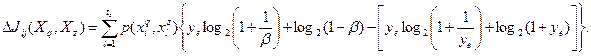 (5а) (5а)
Докажем, что 
На рис. 2. даны графики  и и 
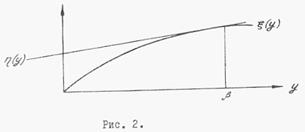
Очевидно, что  и и   т.е. в точке т.е. в точке  кривые кривые  и и  касаются. Покажем, что левее и правее точки касаются. Покажем, что левее и правее точки  разница разница  и и  положительна. Для этого разложим функцию положительна. Для этого разложим функцию  в ряд Тейлора в ряд Тейлора  . Получим . Получим 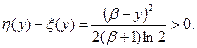 Единственность точки касания следует из графиков Единственность точки касания следует из графиков  и и  . .
Если  , то , то  , т.е. , т.е.  для для  или или  . Отсюда следует, что . Отсюда следует, что  и это доказывает свойство. и это доказывает свойство.
5. Если  , то множества объектов , то множества объектов  и и  максимально различны по признаку максимально различны по признаку  . .
Используя обозначения, принятые при доказательстве свойства 4, нетрудно показать, что 
Из равенства  следует, что следует, что
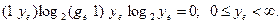
Это равенство выполняется только тогда, когда  или или 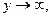 т.е. при условии, если т.е. при условии, если 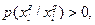 то то  и наоборот. Отсюда следует, что и наоборот. Отсюда следует, что  – пустое множество, т.е. – пустое множество, т.е.  и и  максимально различны по признаку максимально различны по признаку  . .
Пример 1. Группе опрошенных задавали два вопроса: «Ваш возраст?» и «Чем Вы занимаетесь в свободное время?». Было введено несколько возрастных групп  и две группы и две группы 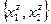 по видам занятий в свободное время. по видам занятий в свободное время.
К первой группе по признаку  , относились те, кто предпочитал в свободное время заниматься спортом, совершать прогулки, любил бывать на улице. Ко второй группе относились домоседы, предпочитавшие быть в кругу семьи. К первой возрастной группе , относились те, кто предпочитал в свободное время заниматься спортом, совершать прогулки, любил бывать на улице. Ко второй группе относились домоседы, предпочитавшие быть в кругу семьи. К первой возрастной группе  относились самые молодые из опрошенных, к последней относились самые молодые из опрошенных, к последней 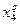 - самые старшие. - самые старшие.
Замерим разницу между различными возрастными группами опрошенных по признаку  , если известно, что распределение условных вероятностей имеет следующий вид: , если известно, что распределение условных вероятностей имеет следующий вид:
 
 
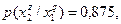 
 
Здесь  - вероятность того, что член возрастной группы - вероятность того, что член возрастной группы 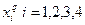 предпочитает занятие предпочитает занятие  в свободное от работы время. в свободное от работы время.
Разница между различными возрастными группами измеряется с помощью меры различия  Результаты удобно представить в виде следующей таблицы. Результаты удобно представить в виде следующей таблицы.
Таблица 1.
| № группы
| 
| 
| 
| 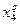
| 
|
| 0,0551
| 0,4058
| 0,4556
| 
| 0,0551
|
| 0,2740
| 0,4058
| 
| 0,4058
| 0,2740
|
| 0,0559
| 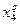
| 0,4556
| 0,4058
| 0,0551
|
| Здесь  стоит на пересечении строки i со столбцом j. Видим, что наиболее далекими по признаку стоит на пересечении строки i со столбцом j. Видим, что наиболее далекими по признаку  оказались группы оказались группы  и и 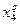 , т.е. самые молодые из опрошенных и самые старшие. Это же было видно и из распределений условных вероятностей, помещенных выше. Наиболее похожи друг на друга группы , т.е. самые молодые из опрошенных и самые старшие. Это же было видно и из распределений условных вероятностей, помещенных выше. Наиболее похожи друг на друга группы  и и  , что объясняется их близостью друг к другу по возрасту, а также группы , что объясняется их близостью друг к другу по возрасту, а также группы  и и 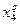 . .
Может возникнуть вопрос об области применения, продемонстрированной на данном примере методики.
По-видимому, настоящий аппарат может быть применен в тех случаях, когда различия между группами объектов по некоторому
признаку (или комплексу признаков) заранее не очевидны и мера различия может быть замерена экспериментально, кроме того, в поиске полярных, т.е. наиболее удаленных или наиболее близких по некоторому признаку групп объектов, а также в поиске таких признаков, по которым данные пары объектов наиболее различались бы, и т.д.
Разностное информационное отношение обладает тем свойством, что с его помощью можно сравнивать отдельные объекты на схожесть друг с другом по некоторому признаку  . .
Покажем это. Пусть имеются объекты  и и  . Признак . Признак  принимает на объекте принимает на объекте  множество значений множество значений  а на объекте а на объекте  множество значений множество значений 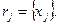 Иными словами на вопрос Иными словами на вопрос  опрашиваемый опрашиваемый  дает дает  ответов, а опрашиваемый ответов, а опрашиваемый  дает дает  ответов. Допустим, что опрашиваемые ответов. Допустим, что опрашиваемые  и и  дают m одинаковых ответов на вопрос дают m одинаковых ответов на вопрос  . Тогда множество . Тогда множество  будет иметь m элементов. будет иметь m элементов.
Введем 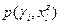 - вероятность того, что - вероятность того, что  на объекте на объекте  примет значение примет значение  , и , и  , которая понимается аналогично. Определим также , которая понимается аналогично. Определим также 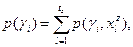

Очевидно, что
если  , то , то 
если  , то , то 
если  , то , то 
если  , то , то 
Формула (7) для данного случая имеет вид
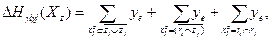
где

Используя значения вероятностей, можно показать, что два первых члена в (9) равны нулю, а третий равен  Итак, Итак,
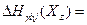 
Очевидно, что  и и  . Подставляя в (6) . Подставляя в (6)  и и  вместо вместо  и и  соответственно и используя (4, 5), получим соответственно и используя (4, 5), получим
 (7) (7)
Это и есть мера различия между двумя объектами.
Пример.
Допустим, что   . Отсюда следует, что . Отсюда следует, что 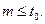 Если Если  и и 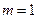 , то , то  . Если же Если . Если же Если  и и  , то , то  . .
В первом случае объекты совпадают по  , а во втором случае они различны, т.е. если признак , а во втором случае они различны, т.е. если признак  может принимать на объекте не более одного значения, то объекты по такому признаку могут быть либо одинаковыми, либо максимально различными. может принимать на объекте не более одного значения, то объекты по такому признаку могут быть либо одинаковыми, либо максимально различными.
Пример 2. Петру и Юрию задали вопрос: «На какие издания Вы подписались в этом году?» Петр сказал, что он выписал «Известия», «Комсомольскую правду», «Техника-молодежи», «Новый мир», и «Советский спорт». Юрий ответил что он будет получать «Правду», «Новый мир», «Советский спорт», «Советский экран» и «Новое время».
Замерим различие между Юрием и Петром. Количество ответов, данное Петром на поставленный вопрос, будет  Количество ответов, данное Юрием на поставленный вопрос, будет Количество ответов, данное Юрием на поставленный вопрос, будет  Количество совпадающих ответов, данных Юрием и Петром, будет Количество совпадающих ответов, данных Юрием и Петром, будет  Теперь по формуле (7) вычислим значение различия между ответами Юрия и Петра - QЮП=0,6. Если бы Юрий и Петр подписались на одни и те же газеты и журналы, то QЮП=0. Если же Юрий подписался не на те газеты и журналы, на которые подписался Петр, то QЮП=1. Теперь по формуле (7) вычислим значение различия между ответами Юрия и Петра - QЮП=0,6. Если бы Юрий и Петр подписались на одни и те же газеты и журналы, то QЮП=0. Если же Юрий подписался не на те газеты и журналы, на которые подписался Петр, то QЮП=1.
Естественным обобщением парной меры близости множеств объектов является мера близости для множеств объектов, количество которых больше двух.
Пусть имеется множество множеств объектов  , различающихся по эквивалентному признаку , различающихся по эквивалентному признаку  . Из . Из  выберем произвольные множества объектов выберем произвольные множества объектов  ; ;  . Введем и изучим меру различия между этими множествами по признаку . Введем и изучим меру различия между этими множествами по признаку  . .
Вероятность принадлежности объекта к множеству  обозначим обозначим  Если объект, принадлежащий к Если объект, принадлежащий к  по признаку по признаку  попадает в градацию попадает в градацию  , то вероятность этого события обозначается , то вероятность этого события обозначается  Введем также совместную вероятность Введем также совместную вероятность 
За меру различия множеств   по признаку по признаку  принимается величина принимается величина
 (8) (8)
где 
Докажем основные свойства этой меры.
1. 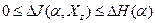 и и 
2. Если множества объектов   одинаковы по одинаковы по  , то , то  и Q=1. Доказательства аналогичны тем, которые даны для парной меры. и Q=1. Доказательства аналогичны тем, которые даны для парной меры.
3. Если множества объектов   максимально различны по максимально различны по  , то , то 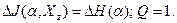 Введем множества градаций Введем множества градаций  по признаку по признаку  , в которые попадают объекты из , в которые попадают объекты из  Из смысла максимального различия множеств Из смысла максимального различия множеств  следует, что следует, что  - пустое множество. Поэтому произвольная градация - пустое множество. Поэтому произвольная градация  может либо принадлежать одному из множеств может либо принадлежать одному из множеств  , либо не принадлежать ни одному из этих множеств. , либо не принадлежать ни одному из этих множеств.
Если  то то 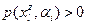 и величина и величина

равна нулю.
Если 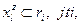 то то  и и  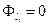 . .
Если же  , то , то  и и 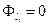 , т.е. , т.е.  , т.к. , т.к. 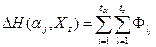 , что доказывает это свойство. , что доказывает это свойство.
4. Если Q=0, т.е. если  , то множества объектов , то множества объектов   максимально одинаковы по признаку максимально одинаковы по признаку  *). *).
5. Если Q=1, т.е. если 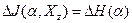 , то множества объектов , то множества объектов   максимально различны по максимально различны по  . Из равенства . Из равенства  и выражения (8) и выражения (8)
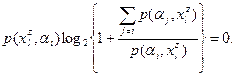
Если 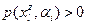 , то необходимо, чтобы , то необходимо, чтобы  и только и только  . .
Если же  , то , то 
Допустим строгое неравенство. Докажем, что в этом случае  принадлежит только одному множеству из принадлежит только одному множеству из 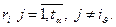
В самом деле, если допустить, что  принадлежит r, то из равенства принадлежит r, то из равенства

следует, что  т.е. т.е.  и только и только 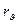 , что и требовалось доказать. , что и требовалось доказать.
В частном случае меры близости для всех множеств  , образованных с использованием признака , образованных с использованием признака  , нетрудно показать, что , нетрудно показать, что  будет выражаться формулой будет выражаться формулой
 (9) (9)
Здесь  - потеря информации - потеря информации  при объединении всех множеств объектов при объединении всех множеств объектов  в одно, равная информации в одно, равная информации  ; ;  - потеря энтропии признака - потеря энтропии признака  , равная , равная  . .
Пример 3. В анкете выпускника содержится вопрос: «Где Вы думаете учиться? (Укажите название учебного заведения)». Исходя из названия учебного заведения, указанного при ответе, школьников можно было разбить на группы по отраслям народного хозяйства и культуры, в которых они, вероятнее всего, должны будут работать по окончании выбранного учебного заведения. Подобное разбиение на группы будем называть разбиением на группы по признаку  , где , где  - символ, присвоенный нами ответу на вышеуказанный вопрос: «Где Вы думаете учиться?» - символ, присвоенный нами ответу на вышеуказанный вопрос: «Где Вы думаете учиться?»
Символом  обозначим признак, обозначающий информацию о том, к какой отрасли относятся учебные заведения, в которые реально попали выпускники после окончания школы. Каждую группу выпускников, полученную в результате разбиения по признаку обозначим признак, обозначающий информацию о том, к какой отрасли относятся учебные заведения, в которые реально попали выпускники после окончания школы. Каждую группу выпускников, полученную в результате разбиения по признаку  , разбивали на подгруппу по признаку , разбивали на подгруппу по признаку  , т.е. производили двухпризнаковую группировку выпускников. Ниже приведены возможные ответы по признакам , т.е. производили двухпризнаковую группировку выпускников. Ниже приведены возможные ответы по признакам  и и  , принятые авторами анкеты. , принятые авторами анкеты.
 ‑ нет ответа; ‑ нет ответа;
 - промышленность тяжелая; - промышленность тяжелая;
 - промышленность легкая; - промышленность легкая;
 - строительство; - строительство;
 - сельское хозяйство - сельское хозяйство
 - лесное –“- - лесное –“-
 - транспорт; - транспорт;
 - связь; - связь;
 - торговля; - торговля;
 - общественное питание; - общественное питание;
 - жилищно-коммунальное хозяйство; - жилищно-коммунальное хозяйство;
 - здравоохранение; - здравоохранение;
 - просвещение; - просвещение;
 - наука; - наука;
 - искусство; - искусство;
 - кредитные учреждения; - кредитные учреждения;
 - аппарат государственного и хозяйственного управления; - аппарат государственного и хозяйственного управления;
 - прочие. - прочие.
Через   обозначим группу выпускников, давших ответ l по признаку обозначим группу выпускников, давших ответ l по признаку  (т.е. выбравших отрасль l, одну из вышеуказанных отраслей), а через (т.е. выбравших отрасль l, одну из вышеуказанных отраслей), а через 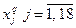 группу выпускников, попавших в отрасль j по признаку группу выпускников, попавших в отрасль j по признаку  . Количество выпускников, давших ответ . Количество выпускников, давших ответ 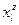 на вопрос на вопрос  , обозначим , обозначим 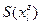 . Аналогично введем . Аналогично введем  . Количество выпускников, планировавших свое будущее в соответствии с ответом . Количество выпускников, планировавших свое будущее в соответствии с ответом  на вопрос на вопрос  и реально попавших в такие учебные заведения, что их ответы по признаку и реально попавших в такие учебные заведения, что их ответы по признаку  оказались оказались 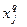 обозначим обозначим  . Например, . Например,  - количество выпускников, планировавших по окончании школы поступить в учебные заведения, готовящие специалистов для тяжелой промышленности, а реально поступивших в учебные заведения связи. - количество выпускников, планировавших по окончании школы поступить в учебные заведения, готовящие специалистов для тяжелой промышленности, а реально поступивших в учебные заведения связи.
Введем условную вероятность того, что опрошенный, давший ответ 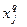 на вопрос на вопрос  , дает ответ , дает ответ 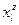 на вопрос на вопрос  . Она равна доле опрошенных, давших ответ . Она равна доле опрошенных, давших ответ 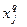 на вопрос на вопрос  и ответ и ответ 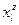 на вопрос на вопрос  , из общего количества людей, давших ответ , из общего количества людей, давших ответ 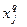 на вопрос на вопрос  , т.е. , т.е. 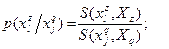 
Таблица условных вероятностей для конкретного случая приведена ниже.
Таблица 2.
| q\z
| 
| 
| 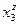
| 
| 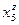
| 
| 
| 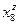
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 0,006
| 0,39
|
|
|
|
|
| 0,06
|
|
|
| 0,06
| 0,06
| 0,37
|
|
|
|
| 
|
|
|
| 0,05
|
|
|
|
|
|
|
|
|
| 0,85
|
| 0,05
|
| 0,05
| 
| 0,18
|
|
| 0,09
|
|
|
|
|
|
|
|
|
| 0,18
| 0,09
|
|
| 0,27
|
В пустых клетках подразумеваются нули; строки и столбцы, состоящие из одних нулей вычеркнуты. Из 18 групп выпускников, полученных при разбиении их на группы по признаку  , рассмотрены лишь 3, так как все остальные группы либо пусты, либо содержат по 3-4 человека. , рассмотрены лишь 3, так как все остальные группы либо пусты, либо содержат по 3-4 человека.
Вычислим общую меру близости по признаку  между группами выпускников, образованными при делении всей совокупности выпускников по признаку между группами выпускников, образованными при делении всей совокупности выпускников по признаку  . Иными словами, определим, насколько близки по своим ответам выпускники, относящиеся к группам . Иными словами, определим, насколько близки по своим ответам выпускники, относящиеся к группам  , ,  , ,  . Вспомним, что эти выпускники, поступившие после окончания школы в учебные заведения, готовящие специалистов для тяжелой промышленности ( . Вспомним, что эти выпускники, поступившие после окончания школы в учебные заведения, готовящие специалистов для тяжелой промышленности (  ), для науки ( ), для науки (  ) и для прочих отраслей ( ) и для прочих отраслей (  ). Вычислим эту меру близости по формуле (9), используя (1) и (3). В нашем слу- ). Вычислим эту меру близости по формуле (9), используя (1) и (3). В нашем слу-
чае  Выше показано, что если Выше показано, что если  , т.е. , т.е. 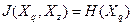 , то выпускники из групп , то выпускники из групп  , ,  , ,  максимально различны по своим ответам на вопрос максимально различны по своим ответам на вопрос  . Т.е. если выпускники из группы . Т.е. если выпускники из группы  дают ответы дают ответы  ответам на вопрос ответам на вопрос  , то ни один человек из группы , то ни один человек из группы  не дает подобных ответов. Например, выпускники из не дает подобных ответов. Например, выпускники из  могут давать в этом случае ответы могут давать в этом случае ответы  а а  - ответы - ответы 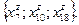 В этом и только случае В этом и только случае  , т.е. группы , т.е. группы  , ,  , ,  максимально различны. Реальная ситуация, как это видно из табл. 1, совершенно иная. Так некоторые члены группы максимально различны. Реальная ситуация, как это видно из табл. 1, совершенно иная. Так некоторые члены группы  дают тот же ответ дают тот же ответ  , что и большинство выпускников из , что и большинство выпускников из  . Некоторые члены группы . Некоторые члены группы  дают общие ответы с дают общие ответы с  (это (это  , ,  , ,  ) и с ) и с  (это (это  , ,  , ,  ). Т.е., между группами ). Т.е., между группами  , ,  и и  есть некоторое сходство и это сходство можно заметить с помощью общей меры близости есть некоторое сходство и это сходство можно заметить с помощью общей меры близости 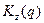 . .
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|


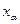 существует множество градаций
существует множество градаций 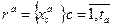 , где
, где  - количество градаций признака
- количество градаций признака  , равное количеству логических возможностей на вопрос, соответствующий признаку
, равное количеству логических возможностей на вопрос, соответствующий признаку  будем обозначать как
будем обозначать как  Очевидно, набор совместных вероятностей признаков
Очевидно, набор совместных вероятностей признаков 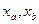 будет
будет  где
где 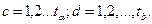 Информация признака
Информация признака  дается формулой.
дается формулой. (1)
(1) ) и
) и  - энтропии признаков
- энтропии признаков  - их совместная энтропия. Свойства этих величин описаны К. Шенноном [1].
- их совместная энтропия. Свойства этих величин описаны К. Шенноном [1]. для данного множества признаков
для данного множества признаков  имеющих множество градаций
имеющих множество градаций  назовем признак, множество градаций которого равно декартовому произведению множеств градаций каждого из признаков
назовем признак, множество градаций которого равно декартовому произведению множеств градаций каждого из признаков 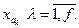
 . Очевидно, что
. Очевидно, что  . Условимся, что разбиение множества объектов на подмножества по признаку
. Условимся, что разбиение множества объектов на подмножества по признаку 
 и
и  по признаку
по признаку  принимается «разностное информационное отношение»
принимается «разностное информационное отношение» (2)
(2) - потеря информации признака
- потеря информации признака  и
и 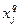 в признаке
в признаке  (3)
(3)

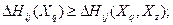 (4)
(4)
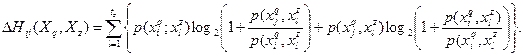 (5)
(5)
 и функция
и функция  выпукла вверх.
выпукла вверх.
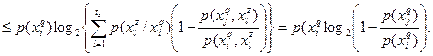
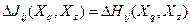 и
и  .
. – пустое множество.
– пустое множество.


 и
и  Введем
Введем 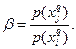 Тогда
Тогда  будет иметь вид
будет иметь вид 

 лежат в заштрихованной области (см. рис. 1).
лежат в заштрихованной области (см. рис. 1). . Это легко доказывается, если использовать определение (2). Очевидно также, что в этом случае
. Это легко доказывается, если использовать определение (2). Очевидно также, что в этом случае  .
. и
и 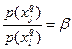 . В них
. В них 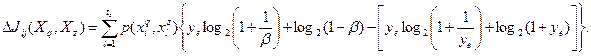 (5а)
(5а)
 и
и 

 и
и 
 т.е. в точке
т.е. в точке  кривые
кривые  касаются. Покажем, что левее и правее точки
касаются. Покажем, что левее и правее точки  в ряд Тейлора
в ряд Тейлора 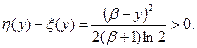 Единственность точки касания следует из графиков
Единственность точки касания следует из графиков  для
для  или
или  . Отсюда следует, что
. Отсюда следует, что  и это доказывает свойство.
и это доказывает свойство.
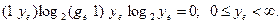
 или
или 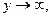 т.е. при условии, если
т.е. при условии, если 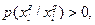 то
то  и наоборот. Отсюда следует, что
и наоборот. Отсюда следует, что  и две группы
и две группы 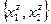 по видам занятий в свободное время.
по видам занятий в свободное время. относились самые молодые из опрошенных, к последней
относились самые молодые из опрошенных, к последней 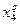 - самые старшие.
- самые старшие.



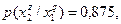



 - вероятность того, что член возрастной группы
- вероятность того, что член возрастной группы 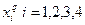 предпочитает занятие
предпочитает занятие  в свободное от работы время.
в свободное от работы время. Результаты удобно представить в виде следующей таблицы.
Результаты удобно представить в виде следующей таблицы.

 стоит на пересечении строки i со столбцом j. Видим, что наиболее далекими по признаку
стоит на пересечении строки i со столбцом j. Видим, что наиболее далекими по признаку  и
и  . Признак
. Признак  а на объекте
а на объекте 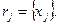 Иными словами на вопрос
Иными словами на вопрос  ответов, а опрашиваемый
ответов, а опрашиваемый  ответов. Допустим, что опрашиваемые
ответов. Допустим, что опрашиваемые 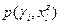 - вероятность того, что
- вероятность того, что  , которая понимается аналогично. Определим также
, которая понимается аналогично. Определим также 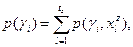

 , то
, то 
 , то
, то 
 , то
, то 
 , то
, то 
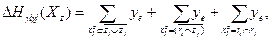

 Итак,
Итак,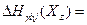
 и
и  . Подставляя в (6)
. Подставляя в (6)  и
и  вместо
вместо  и
и  (7)
(7)
 . Отсюда следует, что
. Отсюда следует, что 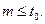 Если
Если  и
и 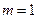 , то
, то  . Если же Если
. Если же Если  , то
, то  Количество ответов, данное Юрием на поставленный вопрос, будет
Количество ответов, данное Юрием на поставленный вопрос, будет  Количество совпадающих ответов, данных Юрием и Петром, будет
Количество совпадающих ответов, данных Юрием и Петром, будет  Теперь по формуле (7) вычислим значение различия между ответами Юрия и Петра - QЮП=0,6. Если бы Юрий и Петр подписались на одни и те же газеты и журналы, то QЮП=0. Если же Юрий подписался не на те газеты и журналы, на которые подписался Петр, то QЮП=1.
Теперь по формуле (7) вычислим значение различия между ответами Юрия и Петра - QЮП=0,6. Если бы Юрий и Петр подписались на одни и те же газеты и журналы, то QЮП=0. Если же Юрий подписался не на те газеты и журналы, на которые подписался Петр, то QЮП=1. , различающихся по эквивалентному признаку
, различающихся по эквивалентному признаку  . Из
. Из  выберем произвольные множества объектов
выберем произвольные множества объектов  ;
;  . Введем и изучим меру различия между этими множествами по признаку
. Введем и изучим меру различия между этими множествами по признаку  Если объект, принадлежащий к
Если объект, принадлежащий к  Введем также совместную вероятность
Введем также совместную вероятность  по признаку
по признаку  (8)
(8)
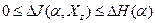 и
и 
 и Q=1. Доказательства аналогичны тем, которые даны для парной меры.
и Q=1. Доказательства аналогичны тем, которые даны для парной меры.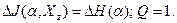 Введем множества градаций
Введем множества градаций  по признаку
по признаку  Из смысла максимального различия множеств
Из смысла максимального различия множеств  - пустое множество. Поэтому произвольная градация
- пустое множество. Поэтому произвольная градация  то
то 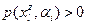 и величина
и величина
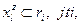 то
то  и
и 
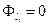 .
. , то
, то  и
и  , т.к.
, т.к. 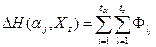 , что доказывает это свойство.
, что доказывает это свойство. , то множества объектов
, то множества объектов 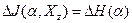 , то множества объектов
, то множества объектов 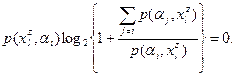
 и только
и только 
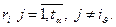

 т.е.
т.е.  и только
и только 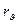 , что и требовалось доказать.
, что и требовалось доказать. , образованных с использованием признака
, образованных с использованием признака  будет выражаться формулой
будет выражаться формулой (9)
(9) - потеря информации
- потеря информации  при объединении всех множеств объектов
при объединении всех множеств объектов  в одно, равная информации
в одно, равная информации  - потеря энтропии признака
- потеря энтропии признака  ‑ нет ответа;
‑ нет ответа; - промышленность тяжелая;
- промышленность тяжелая; - промышленность легкая;
- промышленность легкая; - строительство;
- строительство; - сельское хозяйство
- сельское хозяйство - лесное –“-
- лесное –“- - транспорт;
- транспорт; - связь;
- связь; - торговля;
- торговля; - общественное питание;
- общественное питание; - жилищно-коммунальное хозяйство;
- жилищно-коммунальное хозяйство; - здравоохранение;
- здравоохранение;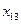 - просвещение;
- просвещение; - наука;
- наука; - искусство;
- искусство; - кредитные учреждения;
- кредитные учреждения; - аппарат государственного и хозяйственного управления;
- аппарат государственного и хозяйственного управления; - прочие.
- прочие. обозначим группу выпускников, давших ответ l по признаку
обозначим группу выпускников, давших ответ l по признаку 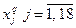 группу выпускников, попавших в отрасль j по признаку
группу выпускников, попавших в отрасль j по признаку 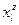 на вопрос
на вопрос 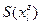 . Аналогично введем
. Аналогично введем  . Количество выпускников, планировавших свое будущее в соответствии с ответом
. Количество выпускников, планировавших свое будущее в соответствии с ответом 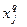 обозначим
обозначим  . Например,
. Например,  - количество выпускников, планировавших по окончании школы поступить в учебные заведения, готовящие специалистов для тяжелой промышленности, а реально поступивших в учебные заведения связи.
- количество выпускников, планировавших по окончании школы поступить в учебные заведения, готовящие специалистов для тяжелой промышленности, а реально поступивших в учебные заведения связи.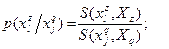



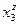

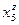


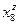












 Выше показано, что если
Выше показано, что если  , т.е.
, т.е. 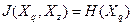 , то выпускники из групп
, то выпускники из групп  ответам на вопрос
ответам на вопрос  а
а 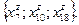 В этом и только случае
В этом и только случае 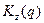 .
.