
|
|
Разбиение множества признаков на подмножества
Запишем матрицу парных информаций вида
Рассмотрим множество элементов столбца i, из которого исключен диагональный элемент. Максимальный элемент этого множества обозначим max Ji. Очевидно, он будет равен максимальной информации, даваемой о признаке і некоторым другим признаком. Образуем множество признаков S, для которых действительно неравенство max Ji ≥ к Н(Xi); 0 < к ≤ 1 едино
95
для всех признаков и выбирается произвольно. Требования на М и N следующие: 1. Для любого признака 2. Количество признаков множества N должно быть минимальным. 3. Должно выполняться равенство М и N удобнее искать на графах парных информаций. Введем множества
Для Хα, неравенство (1) очевидно, так как
Правила построения графов парных информаций: 1. Для столбца 1 матрицы J выделяются Т(1). Если Т(1)≡Х, . то делается шаг 2, иначе признаки 2. На S + 1 шаге для столбца S + 1 матрицы J выделяются T(S+1). Если T(S+1)≡ХS+1, то делается шаг S + 2, иначе признаки, вошедшие в 3. Построение графа кончается на шаге.
Пример. На рис. 1 дана матрица J. На главной диагонали-энтропии признаков. Используя значения энтропий и к =0.8, получаем, что S={Х1, Х2, Х3, Х4, Х5, Х6, Х7, Х8}; Т(1) = {X1}; Т(2) = {X1, X2}; Т(3) = {X1, X4, X3}; Т(4) = {X1, X3, X5, X4}; Т(5) = {Х3, Х7, Х5}; Т(6) = { Х4, Х6}; Т(7) = {Х5, Х7}; Т(8) = {Х4, Х8}; Т(9) = {Х9}.
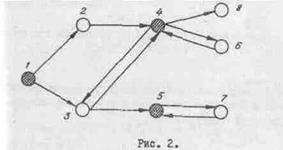
Строится граф с использованием найденных T(i) (i = 1,2,…,9) (см. рис.2).
На графе выбраны множества N = {X1, X2, X3} и M = {X2, X3, X6, X7, X8}. Однако выбор не единствен, так как возможны N = {X1, X4, X7} и M = {X2, X3, X5, X4, X8}.
Объединение подмножества множества α После исключения из α пустых подмножеств и перенумерации получим Пусть пройдено S шагов объединения и делается S + 1 шаг. На шаге S вычислена матрица вида
Рис.3. Здесь 1. В Q(s), исключая диагональные элементы, находится минимальный элемент и соответствующие ему подмножества объединяются. После перенумерации получаем 2. Вычисляется величина
на шаге S + 1, а 3. Если R(s) < R(s+1) то для множества α(s+1) вычисляется матрица Q(s+1) и делается шаг S+2, иначе объединение должно быть прекращено на шаге S. Выведем некоторые свойства, необходимые для алгоритма объединения. Обозначим минимальный элемент Q(s), найденный по пункту 1, как
Здесь
4. Если Если Если Докажем только первое утверждение.
Из (1) и (3) следует, что Используя (4) и равенство 5. Если Если покажем, что После несложного преобразования это неравенство переходит в первое условие. 6. Если Доказывается аналогично свойству 5. 7. Если на первом шаге объединения
Очевидно, что Напишем матрицу вида
Из Q(1) видно, что подмножества объектов Объединим подмножества
Составим матрицу
Так как элемент Если объединить последние две градации в Х(3), то получим признак График
Очевидно, что при S = 3 следует прекратить объединение подмножеств объектов. Выпишем для иллюстрации распределения условных вероятностей до и после объединения. До объединения:
После объединения:
Дополним список свойств разностного информационного отношения. 1. Если множество объектов αi одинаково по Xz с множествами αj и αk, то множества объектов αj и αk одинаковы по Xz. Если Qij(Xq,Xz) = Qik(Xq,Xz) = 0, то Qjk(Xq,Xz) = 0. На основании свойства 4 пишем, что
Следующее ниже свойство 2 означает, что если в М есть признак, не зависящий от множества признаков Выделим из М признак Хψ и образуем множество Мψ , которое есть М без Хψ и имеет эквивалентный
2. Если признак Хψ независим от эквивалентного признака множества
Пусть
Из независимости Хψ от
Подставляя последнее в формулу для Выделим из множества F признаков N признак Хψ и образуем Nφ, которое есть N без Хφ. Эквивалентный признак Nφ назовем
Рассмотрим множества объектов αij и αik, которые по 3. Если признак Хφ независим от эквивалентного признака множества признаков Из независимости Хφ от Найдем, что
т.е. равенство (6) доказано.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
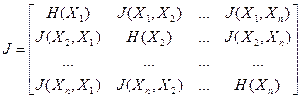
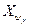 из М должен существовать хотя бы один признак
из М должен существовать хотя бы один признак  из N, такой, что
из N, такой, что  . Очевидно, что при таком условии
. Очевидно, что при таком условии 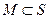
 .
.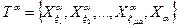
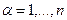 , для элементов которого действительно неравенство
, для элементов которого действительно неравенство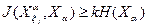 ;
; 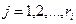 (1)
(1)
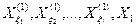 изображаются вершинами графа от вершин признаков
изображаются вершинами графа от вершин признаков 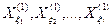 проводятся дуги к вершине признака Х1.
проводятся дуги к вершине признака Х1. , изображаются вершинами графа и от вершин признаков, вошедших в
, изображаются вершинами графа и от вершин признаков, вошедших в 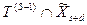 проводятся дуги к вершине признака ХS+1.
проводятся дуги к вершине признака ХS+1.
 . После исключения из rq градаций, соответствующих пустым подмножествам α, и перенумерации получим
. После исключения из rq градаций, соответствующих пустым подмножествам α, и перенумерации получим  и
и  .
.
 – разностное информационное отношение для подмножеств
– разностное информационное отношение для подмножеств 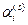 и
и 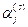 из
из 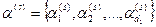 , где αs = d1 – S.
, где αs = d1 – S.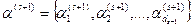 .
. , где
, где 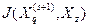 информация признака
информация признака  о признаке Xz
о признаке Xz – их совместная энтропия.
– их совместная энтропия. . Понадобятся следующие равенства:
. Понадобятся следующие равенства: (1)
(1)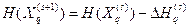 (2)
(2) (3)
(3)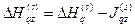 (4)
(4) — потеря информации;
— потеря информации; 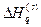 — потеря энтропии;
— потеря энтропии;  — потеря совместной энтропии;
— потеря совместной энтропии; 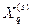 и
и  — признаки при объединении наиболее одинаковых по
— признаки при объединении наиболее одинаковых по 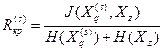
 , то
, то  ;
; ,
,  ;
; ,
, 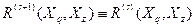
 или
или 
 , получим
, получим 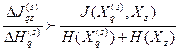
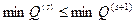 , то
, то 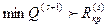 , т.е.
, т.е. 
 то утверждение будет доказано. Используя (1) и (2), получим
то утверждение будет доказано. Используя (1) и (2), получим 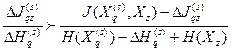
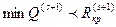 и
и 
 и на каждом шаге объединения выполняется неравенство
и на каждом шаге объединения выполняется неравенство 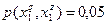 ;
; 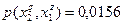 ;
;  ;
; 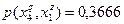 ;
;  ;
;  ;
;  ;
;  .
.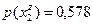 и
и  . Найдем
. Найдем 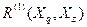 .
.  ,
, 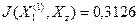 и следовательно
и следовательно 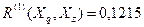 .
.
 и
и  наиболее близки друг к другу по Хz, так как элемент
наиболее близки друг к другу по Хz, так как элемент 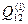 матрицы Q(1) минимален среди недиагональных элементов.
матрицы Q(1) минимален среди недиагональных элементов. с множеством градаций
с множеством градаций 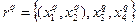 . Здесь
. Здесь 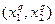 – градация, полученная в результате объединения
– градация, полученная в результате объединения  и
и  . Нетрудно получить:
. Нетрудно получить:  ;
; 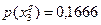 ;
; 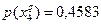 ;
; 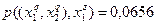 ;
; 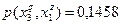 ;
; 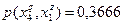 ;
;  ;
; 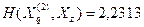 ;
; 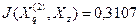 ;
; 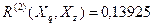
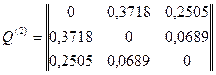
 матрицы Q(2) минимален среди недиагональных элементов, то объединим подмножества объектов α(4) и α(3). Получим признак
матрицы Q(2) минимален среди недиагональных элементов, то объединим подмножества объектов α(4) и α(3). Получим признак  с множеством градаций
с множеством градаций 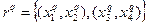 . Не трудно подсчитать, что
. Не трудно подсчитать, что  ;
;  ;
; 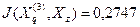 ;
;  ;
;  ;
;  ;
; 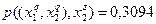 ;
;  .
. с одной градацией. В этом случае
с одной градацией. В этом случае 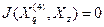 ;
;  и
и 
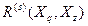 как функции S представлен на рис. 4 и имеет тот же вид, что и на рис. 3. Это понятно, так как
как функции S представлен на рис. 4 и имеет тот же вид, что и на рис. 3. Это понятно, так как 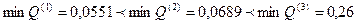 .
.
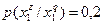 ;
; 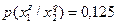 ;
; 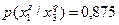 ;
; 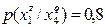 ;
; 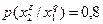 ;
;  ;
;  ;
; 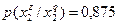 ;
; ;
;  ;
; 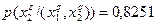 ;
; 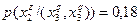 .
.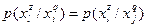 ; l = 1,2,…,tz;
; l = 1,2,…,tz; , откуда
, откуда 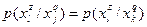 , т.е.
, т.е. 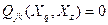 . В частности, отсюда следует, что если, αi – непустое множество и строка (столбец) i в матрице Q(s) нулевая, то матрица Q(s) будет нулевой матрицей.
. В частности, отсюда следует, что если, αi – непустое множество и строка (столбец) i в матрице Q(s) нулевая, то матрица Q(s) будет нулевой матрицей. , то при объединении конечных групп в классы он будет игнорироваться.
, то при объединении конечных групп в классы он будет игнорироваться.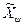 .
. (5)
(5)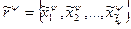 и
и 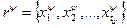 , где
, где  и
и 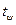 – количества градаций по признакам
– количества градаций по признакам 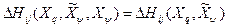 .
.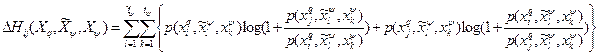
 ,
, 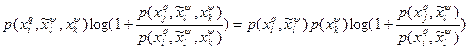
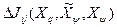 , получим требуемое равенство (10).
, получим требуемое равенство (10). . Введем
. Введем  и
и  .
. , а по признаку Хφ, попадают в градации
, а по признаку Хφ, попадают в градации 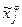 и
и  соответственно.
соответственно.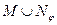 , то
, то 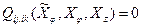 для j,k = 1,2,…,tφ (6)
для j,k = 1,2,…,tφ (6) , т.е. что
, т.е. что 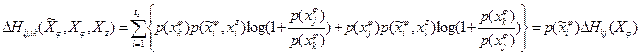
 ;
;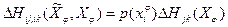 ;
;