
|
|
Потенциальная энергия деформации
Если тело при нагружении испытывает только упругие деформации, то потенциальная энергия деформации численно равна работе сил, затраченных на деформацию тела.
При одноосном напряженном состоянии удельная потенциальная энергия деформации определяется по формуле (3.23) (часть 1)
В общем случае трехмерной задачи выражение для U0 можно записать в виде
Это выражение называется формулой Клапейрона. Удельную потенциальную энергию можно выразить через напряжения, если в (4.34) подставить значения деформаций из закона Гука (4.25). После несложных преобразований получим
Для нахождения полной потенциальной энергии, накапливаемой в теле, необходимо произвести интегрирование по всему объему V тела
Такое разделение энергии на две части необходимо, поскольку, прочность материалов в основном определяется энергией формоизменения. Энергия изменения объема на прочность существенно не влияет. Величина
На основании (4.28) и (4.29) получим
Величина
Выражения (4.35) и (4.40) более просто записываются через главные напряжения
Для двухосновного напряженного состояния формулы (4.35), (4.39), (4.40) преобразуются к виду
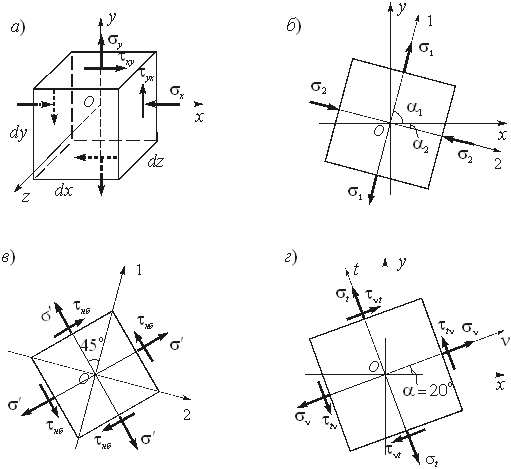
Пример 4.1. В точке тела известны напряжения на площадках, перпендикулярных к координатным осям (рис.4.22,а) sx = - 40 МПа , sу = 160 МПа , tху = 60 МПа , sz = tyz = tzx = 0. Материал - сталь. Модуль упругости и коэффициент Пуассона равны Е = 2,1?105 МПа , n = 0,3.
Установим вид напряженного состояния, который определяется значениями главных напряжений (см. § 4.1). Так как на площадке, перпендикулярной к оси Oz, касательные напряжения равны нулю (tyz = tzx = 0), эта площадка является главной. При этом главное напряжение s3 = sz = 0. Величины других главных напряжений и углы наклона нормалей к главным площадкам определим по формулам (4.8) и (4.9).
s1 = 176,6 МПа , s2 = - 56,6 МПа ;
Поскольку отличными от нуля являются два главных напряжения, напряженное состояние в данной точке тела является двухосным. Положение главных площадок показано на рис.4.22,б. Для контроля правильности вычислений сделаем проверку.
Таким образом, сумма нормальных напряжений на двух взаимно перпендикулярных площадках является постоянной величиной и главные оси напряженного состояния взаимно перпендикулярны. Определим по формуле (4.11) величины наибольших касательных напряжений, которые действуют на площадках с углами наклона ± 45о к главным площадкам (рис.4.22,в).
Нормальные напряжения на этих площадках согласно формуле (4.12) равны:
Определим по формулам (4.4) напряжения на взаимно перпендикулярных площадках с нормалями n и t . Угол наклона нормали n к оси Ox a = = 20о (рис.4.22,г).
ttn На рис.4.23 построен круг Мора, с помощью которого можно графически определить найденные выше напряжения и углы наклона нормалей к площадкам, на которых они действуют. Величины напряжений измеряются с помощью принятого масштаба, а углы наклона нормалей - по транспортиру. Результаты аналитического и графического расчетов совпадают.
Исследуем деформированное состояние тела в окрестности рассматриваемой точки. Определим с помощью закона Гука линейные, угловые и объемную деформации.
Здесь Характер деформаций элементарного параллелепипеда показан на рис.4.24,а,б. Ребра параллелепипеда, параллельные осям Ox и Oz испытывают деформацию укорочения, ребра , параллельные оси Oy - деформацию удлинения. В плоскостях, параллельных плоскости Oxy, происходит искажение прямого угла на величину gху Объем бесконечно малого параллелепипеда увеличивается.
В заключение определим полную удельную потенциальную энергию деформации, энергию изменения объема и энергию изменения формы в окрестности рассматриваемой точки.
- 2?0,3(176,6(- 56,6)] = 0,0962 МПа;

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
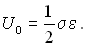

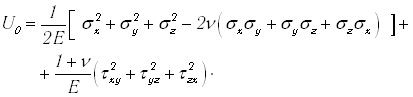
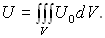
 и энергии изменения формы
и энергии изменения формы 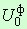 .
.
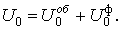
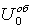 находится аналогично выражению (4.34) как половина суммы произведений средних напряжений s0 , действующих на трех взаимно перпендикулярных площадках, и средних деформаций e0 , определяемых по формулам (4.27), (4.29)
находится аналогично выражению (4.34) как половина суммы произведений средних напряжений s0 , действующих на трех взаимно перпендикулярных площадках, и средних деформаций e0 , определяемых по формулам (4.27), (4.29)

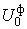 может быть найдена путем вычитания выражения (4.39) из (4.35)
может быть найдена путем вычитания выражения (4.39) из (4.35)
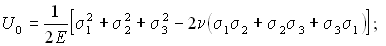

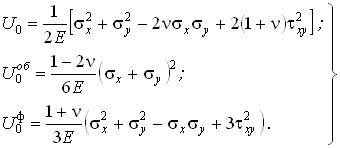
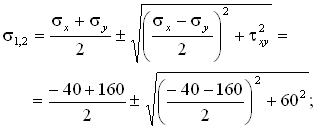
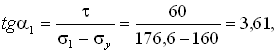
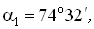

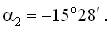
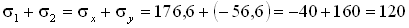 МПа ;
МПа ;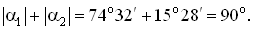
 МПа .
МПа .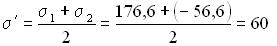 МПа .
МПа .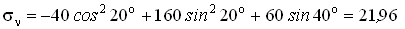 МПа ;
МПа ;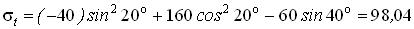 МПа ;
МПа ; МПа .
МПа .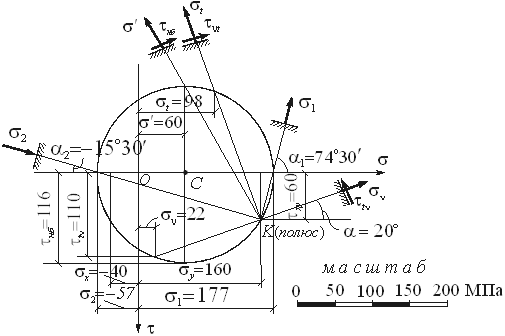
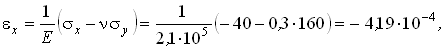
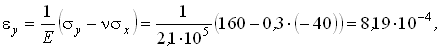
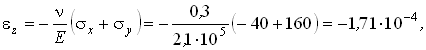
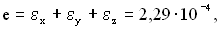
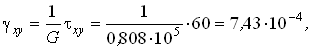
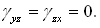
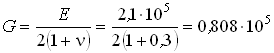 - модуль сдвига.
- модуль сдвига.
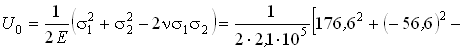
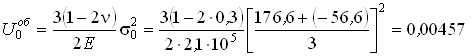 МПа;
МПа;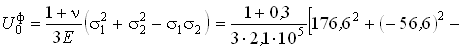
 МПа .
МПа .