
|
|
Определение осевых перемещенийПри центральном растяжении и сжатии прямого стержня поперечные сечения, оставаясь плоскими, получают осевые перемещения u (рис.3.7). Они считаются положительными, если их направление совпадает с положительным направлением оси Ox. Рассмотрим осевые перемещения двух произвольных сечений, отстоящих на расстоянии Dx друг от друга (рис.3.11). После приложения нагрузки эти сечения получают перемещения соответственно u и u + Du. Длина отрезка Dx после деформации составляет Dx1 = Dx + (u + Du) - u = Dx + Du , а величина удлинения равна Dx1 - Dx = Du . Относительная продольная деформация волокон стержня в сечении x представляет собой предел отношения удлинения Du к первоначальной длине Dx при стремлении последней к нулю:
Обозначив в начальном сечении x = 0 u(0) = u0, получим, что постоянная интегрирования C равна u0 . В результате имеем
Учитывая, что на основании (3.6) и (3.5) линейная деформация равна
получим следующую формулу :
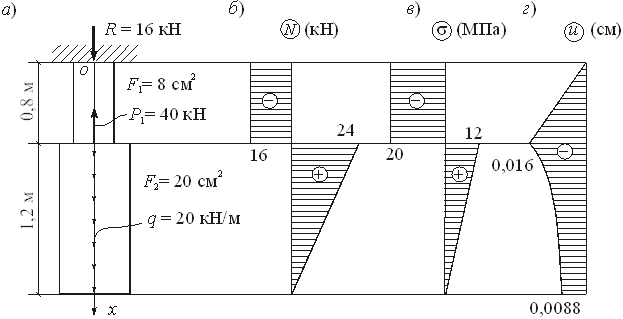
Величина EF называется жесткостью стержня при растяжении и сжатии. Формула (3.11) позволяет установить характер изменения u(x). Для частного случая, когда жесткость EF и продольная сила N являются постоянными величинами, осевые перемещения изменяются по линейному закону.
На участке, где EF = const, а N является линейной функцией, осевые перемещения изменяются по закону квадратной параболы. Если начальное сечение x = 0 закреплено, то u0 = 0. Из соотношения (3.10) следует, что в сечении, где e равно нулю (N = 0), u(x) может иметь экстремум. Удлинение или укорочение стержня длиной l (рис.3.7) равно разности осевых перемещений его концов x = 0 и x = l : Dl = u(l) - u0. Согласно формуле (3.11), получим:
Для частного случая EF = const и N = const, получим
Для стержня с постоянной жесткостью EF и линейным законом изменения продольной силы N при определении Dl удобно использовать геометрический смысл определенного интеграла и привести формулу (3.12) к следующему виду:
где WN – площадь эпюры N на участке от 0 до l.
Статически неопределимые задачи при растяжении и сжатии
Для решения таких задач необходимо составить дополнительные уравнения исходя из рассмотрения деформированного состояния стержня или стержневой системы. Примеры решения статически неопределимых задач, рассмотрены в практикуме. В статически неопределимых системах внутренние усилия и напряжения могут возникнуть не только при силовом, но и при тепловом воздействии (нагреве или охлаждении), а также при монтаже в случае неточного изготовления отдельных элементов и при смещении (осадке) опор. Рассмотрим, например, закрепленный с двух сторон стержень постоянного поперечного сечения, подвергаемый нагреву на величину T (рис.3.16,а). Закрепления препятствуют свободному удлинению стержня. В силу этого возникают две равные по величине и противоположные по направлению опорные реакции R1 = R2 = R. Статически неопределимый стержень при нагреве испытывает сжатие силой N = - R . Для определения продольной силы и напряжений в стержне используем условие его деформации: Dl = DlR + DlT = 0, где DlR = - Rl/EF - возможное укорочение стержня от действия продольной силы N = -R (рис.3.16,б) и DlT = alT - возможное его удлинение при нагреве (рис.3.16,в), где a - коэффициент линейного температурного расширения материала.
Составим уравнение относительно R, решив которое получим:
Напряжения в стержне прямо пропорциональны коэффициенту a, модулю упругости материала E и величине температуры T. При охлаждении статически неопределимого стержня он будет испытывать растяжение. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 .
.
 .
. ,
,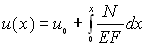 .
.
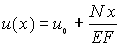 .
. .
.
 .
.
 ,
,

 ,
, 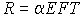 ,
, ,
, .
.