Понятия о расчетных схемах

Задачи технической механики

Техническая и строительная механика составляют близкие по характеру рассматриваемых задач разделы более общей науки – механики деформируемого твердого тела. Излагаемые в технических, в частности, в строительных вузах эти разделы имеют прикладной характер и служат для создания и обоснования методов расчета инженерных сооружений, конструкций и машин на прочность, устойчивость и жесткость при различных внешних воздействиях. Правильное решение этих задач обеспечивает надежность работы сооружений, машин и их конструктивных элементов в течение всего периода эксплуатации.

Например, для стержня, изображенного на рис.1.1,а, первоначальная прямолинейная форма равновесия будет устойчивой до определенного значения сжимающей силы.

Рис.1.1	Рис.1.2

Если сила превысит некоторое критическое значение Р_кр , то устойчивым будет изогнутое состояние стержня (искривленная форма равновесия, рис.1.1,б). При этом стержень будет работать не только на сжатие, но и на изгиб. Такое явление называется потерей устойчивости. Она представляет большую опасность для сооружений и конструкций, так как может вызвать их разрушение в течение короткого промежутка времени.

Жесткость элементов конструкций и сооружений регламентируется нормами проектирования. Например, наибольший прогиб (стрела прогиба f ) применяемых в строительстве балок (рис.1.2) обычно составляет: f = (1/200÷1/1000)l, где l -длина пролета балки.

Решение проблемы надежности конструкции должно сопровождаться поисками наиболее удачных решений с точки зрения эффективности работы конструкции, расхода материалов, технологичности возведения, эстетичности восприятия и т.п.

В курсе сопротивления материалов в основном излагаются методы расчета наиболее простых конструктивных элементов - стержней (балок, брусьев ). При этом используются различные гипотезы, на основании которых выводятся простые расчетные формулы.

Сопротивление материалов базируется на принципах и методах теоретической механики, высшей математики и физики. Большое значение в сопротивлении материалов имеют экспериментальные исследования в лабораторных и натурных условиях.

В строительной механике рассматриваются методы расчета конструктивных систем, состоящих из стержней (стержневых систем). При этом обычно используются все основные положения, результаты и формулы сопротивления материалов для отдельного стержня.

Формирование сопротивления материалов и строительной механики как самостоятельных разделов механики деформируемого твердого тела, началось в первой половине прошлого столетия, что было вызвано интенсивным развитием промышленности и строительством железных дорог.

Запросы инженерной практики дали импульс проведению экспериментальных и теоретических исследований в области прочности и надежности конструкций, сооружений и машин. Ученые и инженеры разработали в прошлом веке различные методы расчета конструкций, правда не всегда обоснованные и требовавшие дальнейшего развития и совершенствования.

Строительная механика стержневых систем выделилась из сопротивления материалов в качестве самостоятельной науки в конце прошлого века в связи с усложнением строительных и машиностроительных конструкций и необходимостью разработки специальных методов их расчета. Интенсивно развивались важные разделы строительной механики - динамика и устойчивость сооружений.

Теоретические методы расчета конструкций и сооружений могут считаться достоверными и надежными, если они проверены с помощью экспериментальных исследований на моделях и в натурных условиях на реальных объектах, а также подтверждены многолетней инженерной практикой. В связи с этим экспериментальные методы исследования конструкций составляют большой раздел сопротивления материалов и строительной механики и им придается большое значение.

Сопротивление материалов, строительная механика стержневых систем и другие разделы механики деформируемого твердого тела являются постоянно развивающимися отраслями современной науки. Создаются новые и совершенствуются существующие методы расчета конструкций. Особенно интенсивно развиваются численные методы решения задач, позволяющие использовать алгоритмы и программы для ЭВМ.

Основные понятия, гипотезы и принципы

Одним из основных понятий сопротивления материалов и строительной механики является понятие о деформации тела при различных внешних воздействиях. Деформация твердого тела связана с изменением его размеров и формы. Например, стержень под действием растягивающих сил удлиняется, балка, нагруженная поперечной нагрузкой, изгибается и т.п.

Напомним, что перемещения тела как жесткого целого, то есть без учета его деформации, изучаются в курсе теоретической механики.

При этом по существу не учитывается молекулярное строение вещества, однако при создании теоретических методов расчета конструкций это является вполне допустимым.

Введение гипотезы о сплошности позволяет рассматривать перемещения точек тела как непрерывные функции координат и использовать аппарат математического анализа.

В сопротивлении материалов и строительной механике вводятся различные гипотезы и допущения относительно характера процесса деформирования тела и свойств его материала.

Эта гипотеза, строго говоря, не соответствует действительности, поскольку после разгрузки часть деформаций, пусть даже и очень малая, не исчезает

Свойства материала тела могут быть неодинаковыми в различных точках, что характеризует его неоднородность. В природе все тела являются более или менее неоднородными. Однако, для многих строительных и конструкционных материалов вполне допустимо введение гипотезы об однородности тела, что соответствует осреднению его свойств по всему объему. Примером такого осреднения является использование гипотезы однородности для бетона.

Материал тела имеет определенные физико-механические характеристики.

Свойство анизотропии в той или иной степени имеют все материалы, однако, для некоторых она незначительна и может не учитываться, как, например, для стали. Материалом с сильно выраженной естественной анизотропией является дерево.

Анизотропия свойств материалов может быть создана искусственно для получения требуемого характера работы элементов конструкции. Примерами таких материалов являются широко применяемые в технике стеклопластики и пластмассы.

В большинстве задач сопротивления материалов и строительной механики материал тела считается сплошным, однородным, изотропным и идеально упругим. Введение этих гипотез позволяет существенно упрощать решение задач и является достаточно обоснованным в очень широкой области инженерных расчетов.

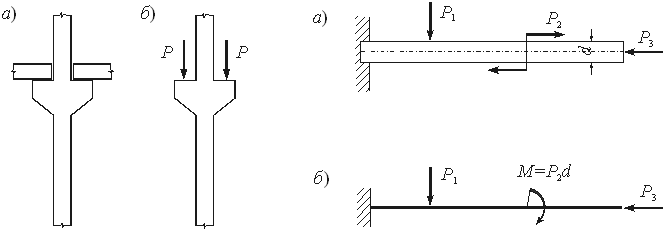
Например, прогиб балки в сечении С от действия двух сил Р₁ и Р₂ рис.1.3,а) согласно этому принципу равен сумме прогибов в этом сечении от раздельного действия сил (рис.1.3,б,в) u_с = u_1с+u_{2c .}

Рис.1.3	Рис.1.4

Отметим, что в некоторых особых случаях принцип независимости действия сил применять нельзя.

Следует также отметить, что при расчете конструкций не всегда возможно использование принципов теоретической механики, таких, например, как перенос силы вдоль линии ее действия, и замена группы сил равнодействующей. Поясним это на двух примерах.

Равновесие стержня, показанного на рис.1.4 не нарушится при переносе точки приложения силы. Не изменится и величина опорной реакции. Однако, в первом случае (рис.1.4,а) деформируется весь стержень, а во втором (рис.1.4,б) — только его нижняя часть.

Замена двух сил равнодействующей не отразится на величине и направлении опорных реакций шарнирно опертой балки (рис.1.5,а,б). Однако, характер изгиба балки при такой замене изменится (изогнутая ось балки на рисунках показана пунктиром).

Понятия о расчетных схемах

Расчет любой конструкции начинается с построения ее расчетной схемы. При этом вводятся различные схематизации и упрощения, касающиеся характера действия нагрузок, условий опирания, типов конструктивных элементов и т.п. Эти упрощения должны быть такими, чтобы расчетная схема отражала все наиболее существенное для характера работы данной конструкции и не содержала второстепенных факторов, мало влияющих на результаты ее расчета.

Рис.1.5	Рис.1.6

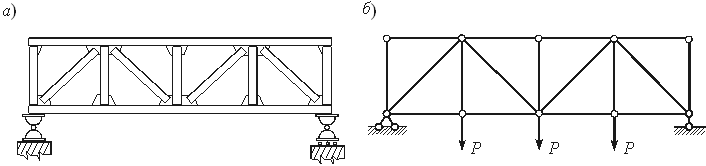
Например, расчетная схема несущей конструкции мостового крана в пролете цеха промышленного здания (рис.1.6,а) может быть представлена в виде шарнирно опертой балки, нагруженной двумя сосредоточенными силами (рис.1.6,б).

При построении расчетной схемы фермы (рис.1.7,а) достаточно жесткое соединение стержней в узлах с помощью металлических листов (фасонок) заменяется шарнирным соединением. Это существенно упрощает расчет фермы и мало влияет на величины усилий в стержнях. Расчетная схема фермы приведена на рис.1.7,б. В большинстве случаев нагрузка передается на ферму в виде сосредоточенных сил, приложенных в узлах. При этом стержни фермы испытывают растяжение или сжатие.

Рис.1.7

Построение и обоснование расчетной схемы составляет ответственный этап проектирования и расчета конструкции. При этом важным является выделение элемента конструкции в соответствующий тип (категорию) по геометрическим соображениям и характеру работы.

К первому типу относятся стержни или брусья (рис.1.8), у которых длина l значительно больше размеров поперечного сечения а, b . Различают стержни сплошного поперечного сечения (рис.1.8,а) и тонкостенные стержни (рис.1.8,б), у которых размеры элементов поперечного сечения b и d имеют разный порядок (например, двутавры и швеллеры).

Геометрическими элементами стержня являются его ось и поперечное сечение.

Рис.1.8	Рис.1.9	Рис.1.10

В зависимости от формы оси стержни могут быть прямыми, кривыми, плоскими и пространственными. Поперечные сечения могут быть одинаковыми или различными по длине (стержни постоянного или переменного сечений). В строительных конструкциях чаще всего используются прямые стержни постоянного или ступенчато постоянного сечения.

В курсе сопротивления материалов часто встречаются термины «волокно» и «слой» стержня.

В инженерных конструкциях широко применяются стержневые системы, состоящие из стержней, соединенных между собой с помощью шарниров или жестких узлов, например, фермы (рис.1.7), рамы (рис.1.9) и арки (рис.1.10). Как уже отмечалось, расчет стержневых систем изучается в основном в курсе строительной механики.

Ко второму типу конструктивных элементов относятся пластины (плиты) и оболочки (рис.1.11,а,б), у которых размеры в плане а и b имеют один порядок и значительно больше третьего размера — толщины h.

Рис.1.11	Рис.1.12

Третьим типом конструктивных элементов является массивное тело, у которого основные размеры а, b и с имеют один порядок (рис.1.12). К таким элементам относятся блоки фундаментов и гидротехнических сооружений, станины машин и т.п.

Расчет пластин, оболочек и тем более массивных тел достаточно сложен и рассматривается в специальных разделах механики деформируемого твердого тела.

При построении расчетных схем существенное упрощение вносит предположение о малости перемещений, связанных с деформацией тела, по сравнению с его размерами. Это предположение позволяет, например, при составлении уравнений равновесия не учитывать изменение положения нагрузки и характера ее действия за счет деформации конструкции. Такой расчет называется расчетом по недеформированной схеме; в некоторых особых случаях его использовать нельзя.

Виды нагрузок

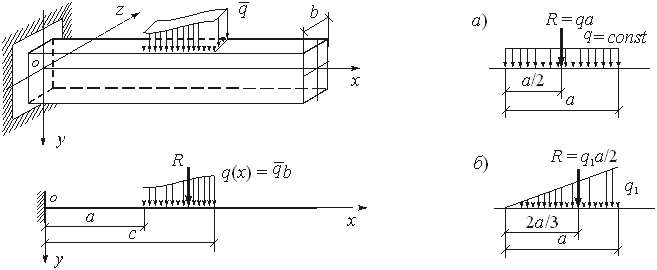
В процессе работы или эксплуатации конструкций, сооружений и машин их элементы испытывают действие различных нагрузок. Нагрузки можно классифицировать по ряду признаков. Рассмотрим некоторые из них.

Нагрузки поверхностные и объемные. Поверхностные нагрузки можно рассматривать как результат взаимодействия различных конструктивных элементов друг с другом или с другими физическими объектами (грунт, вода, снег и т.п.). При построении расчетных схем всегда важно установить характер и последовательность передачи нагрузки от одного конструктивного элемента к другому.

Объемные нагрузки действуют на каждую частицу тела. К таким нагрузкам относятся собственный вес конструкции, силы инерции, силы магнитного притяжения и т.п. В инженерных расчетах объемные нагрузки как правило приводятся к поверхностным нагрузкам, что позволяет существенно упростить расчет.

Нагрузки распределенные и сосредоточенные. Все поверхностные нагрузки являются распределенными по некоторой части поверхности конструкции или ее элементов (рис.1.13). Распределенная нагрузка характеризуется интенсивностью q, которая может быть переменной или постоянной. В последнем случае нагрузка называется равномерно распределенной.

Рис.1.13	Рис.1.14

Распределенные поверхностные нагрузки имеют размерность силы, отнесенной к единице площади, например, Н/м² (Па).

К распределенным поверхностным нагрузкам относятся давление жидкости или газа на стенки резервуара (рис.1.14), давление снега на покрытие здания, напор ветра на конструкцию и т.п.

При расчете стержней распределенная по площади его поверхности нагрузка приводится к линейной нагрузке, распределенной по длине стержня (рис.1.15). Распределенная линейная нагрузка имеет размерность силы, отнесенной к единице длины, например, H/м. Она характеризуется равнодействующей силой, величина которой в общем случае равна

.

(1.1)

Положение линии действия равнодействующей определяется по правилам статики. Приведение к равнодействующей равномерно распределенной нагрузки и нагрузки, изменяющейся по линейному закону, показано на рис.1.16,а,б.

Рис.1.15	Рис.1.16

При малой площади распределения поверхностную нагрузку с той или иной степенью точности можно считать сосредоточенной, как, например, при передаче нагрузки от балок перекрытия к колонне (рис.1.17,а,б). Такая схематизация нагрузки вполне допустима за исключением случаев, когда надо исследовать характер работы конструктивных элементов в самой зоне их взаимодействия.

Рис.1.17	Рис.1.18

Для стержней сосредоточенными нагрузками являются силы и пары сил с равнодействующим моментом, что показано на рис.1.18,а. Расчетная схема стержня в виде оси с приложенными к ней нагрузками приведена на рис.1.18,б.

Рис.1.19

Отметим, что в общем случае нагружения стержня все нагрузки можно разложить на осевые, поперечные и скручивающие составляющие (рис.1.19,а,б,в).

Активные нагрузки и реакции связей. Такое разделение нагрузок важно для построения расчетной схемы и проведения расчета.

Активные нагрузки считаются известными, а величины их заданы, например, в нормах проектирования. Реакции связей возникают в местах закрепления конструктивного элемента (на опорах) и подлежат определению из уравнений равновесия. Если этих уравнений недостаточно для определения опорных реакций, то необходимо составлять дополнительные уравнения исходя, например, из характера или схемы деформации конструкции.

В соответствии с этим расчетные схемы конструкций разделяются на статически определимые и статически неопределимые. Выбор расчетной схемы по этому признаку определяется целым рядом конструктивных, функциональных, технологических и других факторов.

Нагрузки динамические и статические. Статическое нагружение конструкции характеризуется постепенным нарастанием нагрузки до ее конечного значения. При этом силы инерции без ущерба для точности расчета можно не учитывать.

При динамическом нагружении величина и характер действия нагрузки изменяются в течении короткого промежутка времени, как, например, при ударе, либо нагрузка является периодической с малым периодом колебаний (например, вибрационная нагрузка). В этих случаях учет сил инерции и определение частоты колебаний конструкции являются обязательными и составляют важную часть расчета.

Нагрузки постоянные и временные. Такое разделение нагрузок обусловлено методами расчета конструкций, в частности, введением коэффициентов надежности по нагрузке (коэффициентов перегрузки) или коэффициентов запаса.

К постоянным нагрузкам относятся те из них, которые должны действовать на конструкцию в течение всего периода ее эксплуатации (например, собственный вес).

К временным нагрузкам относятся, например, давление людей и оборудования на перекрытие здания, давление снега на крышу, напор ветра и т.п. Эти нагрузки в эксплуатационный период могут существенно изменяться как по величине, так и по характеру действия.

Помимо силовых нагрузок конструкция может испытывать также тепловое воздействие (нагрев или охлаждение), требующего проведения специального расчета.

Не нашли, что искали? Воспользуйтесь поиском по сайту: