
|
|
Определение продольных сил
Центральное растяжение и сжатие прямого стержня вызывается действием осевых нагрузок. В их состав входят сосредоточенные силы и нагрузки, распределенные по длине всего стержня или его некоторого участка (рис.3.1). При постоянной интенсивности q = const нагрузка называется равномерно распределенной, равнодействующая которой равна qa , где a - длина участка распределения. В качестве распределенной осевой нагрузки часто рассматривается собственный вес стержня q = gF, где g - объемный вес материала стержня и F - площадь его поперечного сечения. В местах закрепления стержня при нагружении возникают опорные реакции, подлежащие определению из уравнения равновесия aX = 0.
При центральном растяжении и сжатии прямого стержня в его поперечных сечениях действует только одно внутреннее усилие - продольная сила N, определяемая с помощью метода сечений. Определим, например, продольную силу в поперечном сечении произвольно нагруженного стержня (рис.3.2,а). Для этого надо отбросить мысленно любую часть стержня, а ее влияние на оставшуюся часть заменить действием продольной силы N (рис.3.2,б,в). Из уравнения равновесия левой части находим aX = 0, Для правой части имеем: - qa + P3 - N = 0, Поскольку стержень находится в равновесии, значения N, вычисленные для левой и правой частей должны совпадать.
В общем случае продольная сила изменяется по длине стержня. Ее график, построенный в соответствующем масштабе на оси стержня, называется эпюрой продольных сил. При построении эпюры N удобно использовать дифференциальное соотношение между N и интенсивностью распределенной осевой нагрузки q. Для вывода этого соотношения рассмотрим равновесие бесконечно малого элемента стержня dx , выделенного на участке с распределенной нагрузкой (рис.3.4). На участке dx продольная сила получает приращение dN. Величину q можно в пределах элемента считать постоянной. Составив уравнение равновесия, получим
Из соотношения (3.1) следует, например, что на участках стержня, где q = 0, продольная сила имеет постоянное значение, а на участках, где q = const, N изменяется по линейному закону. Деформации и напряжения
Характер деформации прямого стержня при центральном растяжении и сжатии можно исследовать с помощью опыта на резиновой модели прямоугольного сечения с нанесенной на боковой поверхности, в средней части, прямоугольной сеткой (рис.3.6,а). После приложения растягивающих сил сетка растягивается в осевом направлении и сжимается в поперечном направлении (рис.3.6,б). При этом поперечные линии остаются прямыми и перпендикулярными к оси стержня.
Данный опыт позволяет считать, что поперечные сечения стержня остаются плоскими и перпендикулярными к оси, что соответствует гипотезе плоских сечений. Таким образом, при растяжении и сжатии стержня изменяются его длина и размеры поперечного сечения. Рассмотрим деформированное состояние стержня, закрепленного на левом торце и находящегося под действием растягивающей силы P (рис.3.7,а).
Величина удлинения стержня составляет Dl = l1 - l , а уменьшение поперечного размера равно Db = b - b1 . Определим относительные линейные деформации в продольном и поперечном направлениях, которые равны отношениям Dl и Db к первоначальным размерам:
Поперечные и продольные деформации связаны между собой соотношением
Он определяется экспериментально из опытов на растяжение и сжатие по формуле
В силу гипотезы плоских сечений продольные деформации всех волокон стержня при центральном растяжении и сжатии являются одинаковыми. Из этого можно сделать вывод, что в поперечных сечениях стержня действуют только нормальные напряжения, одинаковые во всех точках сечения (рис.3.7,б,в). Равнодействующей этих напряжений является продольная сила N , которая равна
Отсюда получаем формулу для определения нормальных напряжений
где F - площадь поперечного сечения стержня. Для большинства материалов при малых деформациях справедлива линейная зависимость между напряжениями и деформациями, называемая законом Гука. При растяжении и сжатии стержня закон Гука имеет следующий вид
Значения модуля упругости и коэффициента Пуассона для некоторых материалов приведены в таблице 3.1. Определим напряжения в сечении, проведенном под углом a к оси Ox (рис.3.8,а). Разложив силу N по направлению нормали n и касательной t, получим:
Т а б л и ц а 3.1
Этим составляющим соответствуют нормальные и касательные напряжения в наклонном сечении. Считая, что напряжения распределены по сечению равномерно (рис.3.8,б) и разделив Na и Ta на площадь наклонного сечения Fa = = F/cosa , получим следующие формулы:
где s = N/F - нормальное напряжение в поперечном сечении.
Сделанное на основании гипотезы плоских сечений предположение о равномерном распределении нормальных напряжений по поперечному сечению справедливо не во всех случаях. В сечениях, близких к местам приложения сосредоточенных сил, при резком или скачкообразном изменении площади или формы поперечного сечения характер распределения напряжений по сечению является более сложным. Например, вблизи нагруженного торца стержня распределение напряжений является существенно неравномерным и зависит от способа приложения нагрузки (рис.3.9,а,б). Однако, на достаточном удалении от торца распределение напряжений становится почти равномерным и одинаковым для обоих случаев. Этот вывод следует из известного в механике принципа Сен-Венана.
Например, в растянутой полосе прямоугольного сечения с круглым отверстием на оси Ox (рис.3.10) наибольшие напряжения при d << h в три раза больше, чем по неослабленному сечению.
Концентрация напряжений особенно опасна для прочности элементов конструкций из хрупких материалов. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|


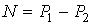 .
. .
.
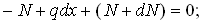



 ,
,  .
.
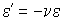 .
.
 .
.
 .
. ,
,
 .
.



