
|
|
Одноосное напряженное состояние.
Этот случай соответствует, например, задаче центрального растяжения и сжатия, рассмотренной в главе 3 (часть 1). Формулы для напряжений на наклонных площадках (см. формулы (3.8), часть 1) можно получить из формул (4.10) для двухосного напряженного состояния, если положить в них s1 = s, s2 = 0 :
В этих формулах a - угол между нормалью n к наклонной площадке и направлением действия напряжения s (рис.4.11). Определение напряжений с помощью круга Мора
Между формулами (4.4) для напряжений на наклонных площадках при двухосном напряженном состоянии и формулами (2.7) (часть 1) для определения моментов инерции при повороте осей существует очевидная аналогия. Переход от одних формул к другим может быть осуществлен с помощью следующих замен:
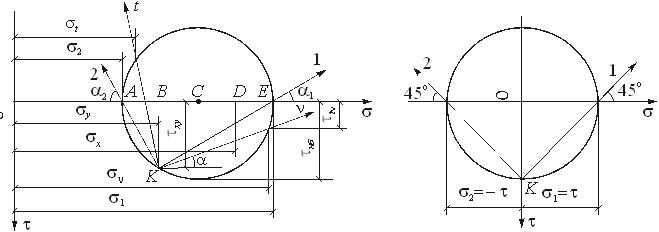
Поэтому графический способ определения моментов инерции с помощью круга Мора может быть также использован для исследования напряжений при двухосном напряженном состоянии. Круг Мора для напряжений (рис.4.13) строится аналогично кругу Мора для моментов инерции (рис.2.19, часть 1) с той разницей, что при выбранном на рис.4.12 направлении осей координат Ox и Oy положительные значения касательных напряжений откладываются вниз от горизонтальной оси. Заметим также, что в отличие от осевых моментов инерции нормальные напряжения могут быть как положительными, так и отрицательными величинами. Поэтому центр круга Мора для напряжений может быть расположен как справа, так и слева от вертикальной оси.
На рис.4.13 с помощью круга Мора определены главные напряжения s1 и s2 , действующие на площадках с нормалями, составляющими с осью Ox углы a1 и a2 (рис.4.12,б), а также нормальные и касательные напряжения, действующие на произвольных площадках с нормалями n и t (рис.4.12,в).
В качестве примера определения напряжений с помощью круга Мора рассмотрим задачу о чистом сдвиге, изображенную на рис.4.10,а. Поскольку в этом случае sх = sу = 0, то точка K лежит на оси tху , а центр круга C совпадает с началом координат O (рис.4.14). Очевидно, что главные напряжения при чистом сдвиге равны ± t , а главные площадки расположены под углами ± 45о к исходным площадкам. Перемещения и деформации
Под действием внешних сил происходит деформирование тела и перемещение его точек в пространстве. При этом возможны перемещения двух видов: перемещение тела как абсолютно твердого без изменения его формы и размеров и перемещения, связанные с деформированием тела. Перемещения первого вида изучаются в теоретической механике. Поэтому в дальнейшем рассматриваются только перемещения, связанные с деформированием тела. Пусть в результате деформирования тела точка A переместилась в новое положение A' (рис.4.15). Обозначим составляющие вектора полного перемещения AA' по осям Ox, Oy, Oz соответственно через u, v, w. Перемещения u, v , w считаются положительными, если они происходят в положительном направлении осей координат. Будем полагать, что перемещения малы по сравнению со всеми характерными размерами тела. Например, прогибы балок, применяемых в строительных конструкциях, обычно малы по сравнению с длиной балки и размерами поперечного сечения. Перемещения различных точек тела различны и являются непрерывными функциями координат x, y, z:
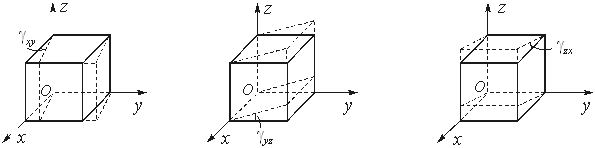
Для исследования деформаций вырежем мысленно вблизи произвольной точки тела элементарный параллелепипед с ребрами dx, dy, dz. В результате различия перемещений точек параллелепипеда его ребра удлиняются или укорачиваются а первоначальные углы между ребрами искажаются. В соответствии с этим различают два основных вида деформаций - линейные и угловые.
Деформации удлинения считаются положительными, а укорочения - отрицательными. Используя эти соотношения, можно найти длины ребер dx1, dy1, dz1 после деформации:
При этом индексы указывают, в какой плоскости происходит угловая деформация. Заметим, что напряженное и деформированное состояния элементарного параллелепипеда для трех случаев, изображенных на рис.4.18,а,б,в (показаны проекции параллелепипеда на плоскость Oxy), одинаковы, так как эти три случая отличаются друг от друга только величинами жесткого вращения вокруг оси Oz, не вызывающего дополнительных напряжений.
Деформации сдвига так же, как касательные напряжения, обладают свойством взаимности, то есть
В дальнейшем будем считать, что линейные и угловые деформации по абсолютной величине существенно малы по сравнению с единицей, то есть
Деформации, связанные с искривлением граней и ребер элементарного параллелепипеда, являются величинами более высокого порядка малости по сравнению с рассмотренными основными деформациями и их можно не учитывать.
где Учитывая формулы (4.14), найдем
Отбрасывая в этом выражении произведения деформаций, как величины второго и третьего порядков малости, по формуле (4.15) окончательно получим
Таким образом, объемная деформация равна сумме трех линейных деформаций.
Аналогично тензору напряжений (4.2) введем понятие тензора деформаций
Тензоры напряжений и деформаций имеют аналогичную структуру и могут быть получены один из другого с помощью следующих формальных замен:
Соответствующие формулы для напряжений и деформаций также имеют аналогичную структуру.
Главные деформации обозначаются через e1 , e2 , e3 , при этом принимается, что e1 > e2 > e3 . В изотропном теле, свойства которого не зависят от направлений, главные оси напряженного и деформированного состояний совпадают. Обобщенный закон Гука
Для получения полной системы уравнений, описывающих напряженное и деформированное состояния тела, необходимо иметь равенства, связывающие между собой напряжения и деформации. В эти равенства должны входить величины, характеризующие физические свойства материала. В общем случае трехосного напряженного состояния на всех гранях элементарного параллелепипеда, выделенного в окрестности произвольной точки тела, действуют нормальные и касательные напряжения (на рис.4.19 показаны напряжения только на видимых гранях).
Будем предполагать, что напряжения и деформации связаны между собой линейными зависимостями и любая деформация, вызванная одновременным действием нескольких напряжений, на основании принципа независимости действия сил может быть найдена как сумма деформаций от действия каждого из напряжений в отдельности. В изотропном теле нормальные напряжения вызывают только линейные деформации удлинения или укорочения ребер элементарного параллелепипеда и не вызывают угловых деформаций. Касательные напряжения вызывают только угловые деформации и не вызывают линейных деформаций. На рис.4.20,а,б показано деформированное состояние элементарного параллелепипеда от действия нормального напряжения sx и касательного напряжения tху . Элемент, изображенный на рис.4.20,а, испытывает одноосное напряженное состояние. Под действием напряжения sx возникают деформации удлинения
Здесь n - коэффициент Пуассона. Аналогично под действием напряжений sy и sz возникают деформации
Полную относительную деформацию ребер параллелепипеда, параллельных оси Ox, находим как сумму деформаций от действия каждого из напряжений
Аналогично можно найти относительные деформации ребер, параллельных осям Oy и Oz. Таким образом, линейные деформации связаны с нормальными напряжениями тремя формулами закона Гука
В главных осях формулы (4.19) примут вид
Элемент, изображенный на рис.4.20,б, испытывает напряженное состояние, называемое чистым сдвигом (см. § 4.2). Рассмотрим проекцию элемента на координатную плоскость Oxy (рис.4.21). Главные оси напряженного и деформированного состояний наклонены по отношению к площадкам чистого сдвига под углом 45о. Главные напряжения по абсолютной величине равны касательным напряжениям и имеют противоположные знаки
Для нахождения величин главных деформаций e1 и e2 , которые в рассматриваемом случае представляют собой соответственно относительное удлинение диагонали AC и относительное укорочение диагонали BD, воспользуемся аналогией между формулами напряженного и деформированного состояний. Заменяя в соответствии с (4.18) в формулах (4.21) s1 , s2 , txy на e1 , e2 , gxy2 , получим
Чистый сдвиг представляет собой частный случай двухосного напряженного состояния. Поэтому положим в первой из формул (4.20) s3 = 0 и подставим вместо s1 и s2 их выражения из (4.21), а вместо e1 - выражение из первой формулы (4.22). Тем самым мы свяжем деформации сдвига с касательными напряжениями:
Вводя в этом выражении обозначение
получим одну из формул закона Гука при сдвиге
Аналогично можно получить еще две формулы, связывающие деформации сдвига gуz и gzх с касательными напряжениями tyz и tzx
Величина G называется модулем сдвига.
Таким образом, в общем случае трехосного напряженного состояния имеем шесть формул, устанавливающих связь между напряжениями и деформациями в окрестности точки тела, которые называются обобщенным законом Гука.
Сложим почленно первые три формулы (4.25)
Используем обозначения для объемной деформации e, средней деформации e0 , суммы нормальных напряжений s и среднего напряжения s0
и введем понятие модуля объемной деформации
Тогда равенство (4.26) можно записать в виде
Эти соотношения называют законом упругого изменения объема. Как показывают лабораторные исследования, этот закон справедлив и при высоких значениях среднего напряжения s0 , значительно превышающих предел упругости материала. С помощью (4.28) и (4.29) покажем, что для изотропного материала коэффициент Пуассона не может превышать значение n = 0,5. Пусть ко всем граням элементарного параллелепипеда приложены сжимающие напряжения sх, sу, sz . Если при этом предположить, что n > 0,5, то из формул (4.28) и (4.29) следует, что K < 0 и e > 0 , то есть при всестороннем сжатии объем параллелепипеда увеличивается, что противоречит физическому смыслу.
В случаях двухосного напряженного состояния в формулах (4.25) необходимо положить sz = tyz = tzx = 0. В результате получим
Деформация ez может быть найдена из третьего равенства (4.25)
Деформации сдвига gyz = gzx = 0. Таким образом, при двухосном напряженном состоянии имеем три формулы (4.30) обобщенного закона Гука. В главных осях угловые деформации отсутствуют и формулы (4.30) имеют вид
Если равенства (4.30) решить относительно напряжений, то получим

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

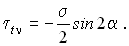
 .
.

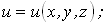
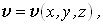
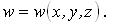




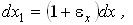
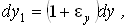
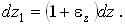
 , g yz , = g zy ,
, g yz , = g zy ,  .
.

 .
.

 и
и  - объемы параллелепипеда до и после деформации.
- объемы параллелепипеда до и после деформации.





 ребер параллелепипеда, параллельных оси Ox , и деформации укорочения
ребер параллелепипеда, параллельных оси Ox , и деформации укорочения  и
и  ребер, параллельных осям Oy и Oz. Эти деформации согласно закону Гука при одноосном напряженном состоянии и зависимости между поперечными и продольными деформациями будут равны (см. § 3.2, часть 1)
ребер, параллельных осям Oy и Oz. Эти деформации согласно закону Гука при одноосном напряженном состоянии и зависимости между поперечными и продольными деформациями будут равны (см. § 3.2, часть 1)
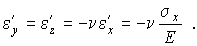

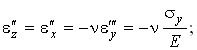
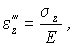
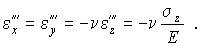
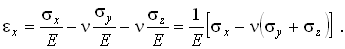



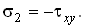



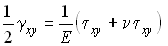 .
.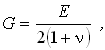

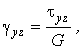
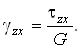









 , e ® 0 . То есть изменения объема не происходит. Материал, обладающий этим свойством, называется несжимаемым.
, e ® 0 . То есть изменения объема не происходит. Материал, обладающий этим свойством, называется несжимаемым.


