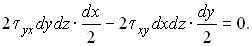Напряженное состояние в окрестности точки тела и его виды

Под действием внешних сил, приложенных к телу, в нем возникают внутренние силы, которые определяются величинами нормальных и касательных напряжений в каждой точке тела.

Вырежем мысленно в окрестности произвольной точки тела (рис.4.1) элементарный параллелепипед с размерами dx, dy, dz (рис.4.2). Вектор полного напряжения на каждой грани можно разложить на три составляющих по координатным осям. Например, на грани, перпендикулярной к оси Ox, этими составляющими являются нормальное напряжение s_x и касательные напряжения t_yx и t_zx . Индекс у нормального напряжения указывает нормаль к площадке, на которой оно действует. Первый индекс у касательного напряжения обозначает ось, параллельно которой оно направлено, а второй - нормаль к площадке, на которой оно действует.

Рис4.1	Рис.4.2

Напряжения являются непрерывными функциями координат точек тела. Вследствие малости элементарного параллелепипеда можно считать, что напряжения на его параллельных гранях одинаковы по величине и равномерно распределены по площадкам граней.

Для касательных напряжений применяется следующее правило знаков.

На рис.4.2 показаны положительные напряжения.

Составим уравнения моментов сил, действующих на элементарный параллелепипед, относительно оси, проходящей через центры горизонтальных граней. Для этого нужно равнодействующие касательных напряжений t_yxdydz и t_xydxdz, действующих на вертикальных гранях, умножить на расстояния от центров этих граней до указанной оси:

Из этого равенства получим t_ух = t_ху. Точно также можно получить еще два аналогичных равенства. В результате будем иметь следующие три соотношения:

(4.1)

В силу закона парности на трех взаимно перпендикулярных площадках, проведенных через точку тела, имеем шесть искомых напряжений s_х ,s_у ,s_z , t_ху, t_уz ,t_zx . Совокупность этих напряжений представим в виде матрицы

(4.2)

которая называется тензором напряжений.

Можно показать, что указанные шесть напряжений полностью определяют напряженное состояние в окрестности рассматриваемой точки тела. Это означает, что зная эти шесть величин можно найти напряжения на любой наклонной площадке, проходящей через данную точку. Следовательно, напряженное состояние в окрестности точки характеризуется тензором напряжений. Известно понятие числа и понятие вектора, как величины, определяемой тремя числами. Напряженное состояние определяется уже не тремя, а шестью числами и представляет собой тензор. Тензору напряжений в отличие от вектора нельзя дать простое геометрическое толкование.

Обозначим величины главных напряжений через s₁, s₂, s₃ . При этом будем считать, что s₁ ³ s₂ ³ s₃ .

Главные напряжения являются экстремальными величинами. Напряжение s₁ представляет собой наибольшее, а s₃ - наименьшее среди нормальных напряжений на различных площадках, проходящих через данную точку.

Рис.4.3

На рис.4.3,а показан элементарный параллелепипед, грани которого являются главными площадками, а нормали к ним, оси 1, 2, 3 - главными осями напряженного состояния.

При расчете элементов конструкций на прочность необходимо знать в каждой точке вид напряженного состояния, который характеризуется значениями главных напряжений. Существуют три основных вида напряженного состояния:

Наибольшее по абсолютной величине касательное напряжение действует на площадках, наклоненных под углом 45^o к главным осям 1 и 3, и равно

Не нашли, что искали? Воспользуйтесь поиском по сайту: