
|
|
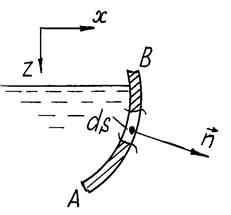
Определение силы давления жидкости на поверхности тел.Задача сводится к нахождению силы давления жидкости на поверхности стенок, ограничивающих ее. Рассмотрим криволинейную поверхность AB произвольной формы, площадь которой S (рис. 3.3). Выделим на ней элементарную площадку dS, пусть
где p - гидростатическое давление в центре площадки. Обычно в технических приложениях интерес представляет лишь сила, возникающая от избыточного давления. Имея в виду, что
На всю площадь действует сила
Запишем это выражение в проекциях на оси координат, что дает
Для удобства изобразим отдельно элементарную площадку (см. рис. 3.4). Из рисунка следует, что
где
Рассмотрим горизонтальную составляющую. Из механики известно, что интеграл (3.18) есть статический момент площади, равный произведению Следовательно,
т.е. горизонтальная составляющая равна произведению вертикальной проекции стенки на гидростатическое давление в центре тяжести этой проекции. Определим теперь вертикальную составляющую силы, для чего воспользуемся следствием из формулы Гаусса-Остроградского (см. ф-лу 1.16)
Из уравнения равновесия (3.2) имеем
Вертикальная проекция единичной массовой силы Следовательно,
V носит название объема тела давления. Таким образом, вертикальная составляющая равна весу жидкости, заключенному в объеме тела давления. Для нахождения этого объема следует использовать формальное правило: тело давления - это объем, образованный криволинейной стенкой, ее проекцией на свободную поверхность (либо на продолжение свободной поверхности) и вертикальными проектирующими плоскостями. На рис. 3.5 показаны примеры определения тел давлений для двух случаев.
Как следует из рисунка, тело давления может быть как положительным, так и отрицательным (фиктивным). Плоская поверхность. Этот случай можно рассматривать как частный предыдущего, но можно получить и более удобное соотношение. Действительно, общее выражение для силы давления имеет вид (3.15), но так как поверхность плоская, то ориентация нормали для всех ее точек остается одинаковой, и, следовательно,
Из формулы (3.22) следует, что
Следовательно, сила давления на плоскую поверхность равна произведению ее площади на гидростатическое давление в центре тяжести этой поверхности. Следует отметить, что задачи, связанные с определением сил давления на поверхности, играют исключительно важную роль в гидротехнической практике. Применительно к энергетике и машиностроению круг этих задач заметно сужается и ограничивается, главным образом, расчетом болтовых соединений люков различных резервуаров, находящихся под давлением.
КИНЕМАТИКА. Приобретение любого познания всегда полезно для ума, ибо он сможет впоследствии отвергнуть бесполезное и сохранить хорошее. Ведь ни одну вещь нельзя ни любить, ни ненавидеть, если сначала ее не познать. Леонардо да Винчи. Кинематика занимается изучением движения жидкости, не интересуясь причинами, которые его вызвали. По образному выражению Н.Е.Жуковского, кинематика изучает «геометрию движения». Принципиально можно пойти двумя путями. По первому из них изучается движение каждой отдельной жидкой частицы. Чтобы выделить ее, в начальный момент времени В настоящем пособии используется главным образом метод Эйлера. Для желающих глубже разобраться в этом вопросе можно рекомендовать книгу: Федяевский К.К., Фаддеев Ю.И. Гидромеханика. - М.: Судостроение, 1968. - 567 с. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
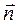 - орт внешней нормали. Сила, действующая на эту площадку
- орт внешней нормали. Сила, действующая на эту площадку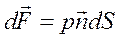
 , получаем
, получаем
 (3.14)
(3.14) (3.15)
(3.15)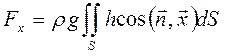 (3.16)
(3.16) (3.17)
(3.17)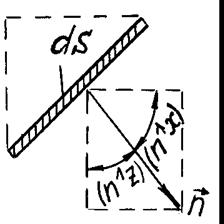
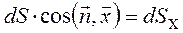
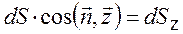
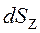 - вертикальная, и
- вертикальная, и 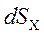 - горизонтальная проекции dS. Таким образом
- горизонтальная проекции dS. Таким образом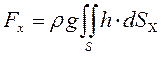 (3.18)
(3.18) (3.19)
(3.19)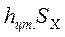 , где
, где 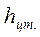 - координата центра тяжести вертикальной проекции.
- координата центра тяжести вертикальной проекции. (3.20)
(3.20)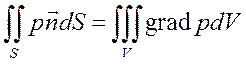
 , т.е.
, т.е.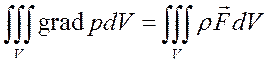
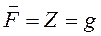 (знак плюс, т.к. в данном случае ось z ориентирована вниз).
(знак плюс, т.к. в данном случае ось z ориентирована вниз).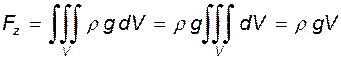 (3.21)
(3.21)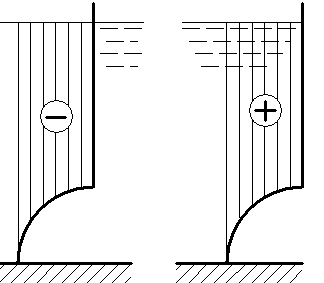
 (3.22)
(3.22) направлена по нормали к стенке, поэтому можно записать
направлена по нормали к стенке, поэтому можно записать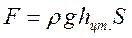 (3.23)
(3.23)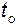 отмечаются ее координаты
отмечаются ее координаты  ,
,  и
и 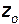 . Движение считается определенным, если в каждый момент времени для каждой частицы известны уравнения, описывающие ее путь во времени, т.е. известны параметрические уравнения траекторий всех частиц. Этот путь предложен Лагранжем. По методу Эйлера изучается изменение скорости и других параметров в точках пространства x, y, z.
. Движение считается определенным, если в каждый момент времени для каждой частицы известны уравнения, описывающие ее путь во времени, т.е. известны параметрические уравнения траекторий всех частиц. Этот путь предложен Лагранжем. По методу Эйлера изучается изменение скорости и других параметров в точках пространства x, y, z.