|
|
Динамическая характеристика автомобиляТяговая диаграмма дает наглядное представление о балансе сил, действующих на автомобиль. Однако для сравнительной оценки тяговых свойств различных автомобилей она неудобна, поскольку при одной и той же величине свободной окружной силы у автомобилей с различным общим весом Ga тяговые свойства будут различными. Для сравнительной оценки тяговых свойств автомобилей, имеющих различный вес, удобнее пользоваться безразмерной величиной D, представляющей собой отношение свободной силы к весу автомобиля. Это отношение называют динамическим фактором.
Если разделить на Ga обе части уравнения (49), то получим уравнение силового баланса в безразмерной форме:
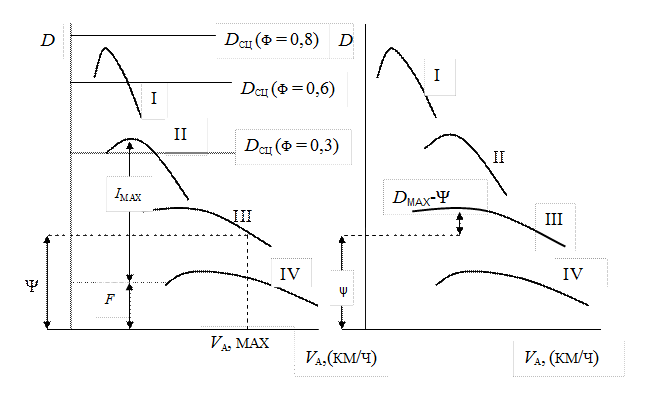
В связи с тем, что и Рсв и Рв являются функциями от Va, то и D = f (Va). Графическую зависимость динамического фактора от скорости называют динамической характеристикой (рис. 15).
а) б) Рис. 15. Динамическая характеристика
При помощи динамической характеристики можно решать все те задачи, которые можно решать при помощи тяговой диаграммы.
Максимальная скорость движения на дороге с заданным ψ (рис. 15а). Поскольку при максимальной скорости ja=0, то уравнение (41) перепишется так: D = ψ. Следовательно, максимальной будет та скорость, при которой динамический фактор равен коэффициенту ψ дорожного сопротивления. Для определения этой скорости по оси ординат отложим заданное значение ψ и проведем из полученной таким образом точки прямую, параллельную оси абсцисс. Абсцисса точки пересечения этой прямой с кривой D = f(Va) и даст искомую максимальную скорость движения. Если автомобиль снабжен карбюраторным двигателем, не имеющим ограничителя оборотов, то кривая D = f(Va) может быть всегда продолжена до пересечения с прямой ψ = Ф(Va) (рис. 15а). Если автомобиль снабжен карбюраторным двигателем, имеющим ограничитель оборотов, либо дизелем, то в случае, когда прямая, соответствующая заданному ψ, не пересекает кривую D = f(Va), величина
Максимальный подъем, преодолеваемый автомобилем с постоянной скоростью (Va = const) на дороге с заданным f на заданной передаче (рис. 15а). В этом случае уравнение (50) запишется так: Разность Dmax-f можно найти графически, отложив по оси ординат величину f и проведя из полученной таким образом точки прямую, параллельную оси абсцисс.
Максимальное ускорение на дороге с заданным ψ на заданной передаче (рис. 15б). Из уравнения (50)
Разность Dmax–ψ можно найти графически, проведя прямую, параллельную оси абсцисс, на расстоянии ψот этой оси. Подобным же образом могут быть решены и другие задачи, указанные выше. Поскольку тяговая сила ограничена сцеплением колеса с дорогой, то и динамический фактор ограничен по сцеплению. Так как буксование колес обычно имеет место при подведении к колесу большой силы тяги и на малых скоростях движения, то в этом случае можно приближенно считать Pсв = Z2φ, где Z2 – нормальная реакция, действующая на ведущие колеса автомобиля. Отношение Для облегчения расчетов в тех случаях, когда автомобиль имеет переменный общий вес, например, в результате изменения полезной нагрузки, профессор Н.А. Яковлев предложил дополнить динамическую характеристику номограммой (рис. 16), которая наносится слева от динамической характеристики и состоит из ряда прямых, позволяющих определить масштаб динамического фактора D по двигателю (сплошные прямые) и динамического фактора Dсц по сцеплению (пунктирные прямые) для любой величины полезной нагрузки от Н = 100% до Н = 0%. График рис. 16 называют динамическим паспортом. По оси абсцисс номограммы откладывается полезная нагрузка Н %, причем Н = 100% соответствует началу координат динамической характеристики. Если при Н = 100% выбран такой масштаб, что D = a соответствует δ мм оси ординат, то при любой другой полезной нагрузке то же значение D(D = a) будет соответствовать H = δH мм оси ординат, причем
где Gа – полный вес автомобиля; Gао – вес автомобиля без полезной нагрузки;
Рис. 16. Динамический паспорт автомобиля
Как видно из формулы (52), зависимость масштаба D от полезной нагрузки Н, выраженной в %, является линейной. Поэтому для построения номограммы масштабов достаточно кроме произвольно выбираемого масштаба при Н = 100%, найти масштаб для любого другого значения Н. Удобнее всего определять значения масштаба для Н = 0. В этом случае Для динамического фактора по сцеплению масштаб выбирается так: при Н = 100% значению Dсц = a соответствует при Н = 0 тому же значению Dсц соответствует Gвед и Gвед0 – вес, приходящийся на ведущие колеса, соответственно при H = 100% и Н = 0 %.
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
. (49)
(50)
определяется кинематически по формуле (7), в которую следует подставить угловую скорость ωno (обороты nno), соответствующую срабатыванию ограничителя.
, где Dmax – максимальный динамический фактор на заданной передаче.
. (51)
называют динамическим фактором по сцеплению. Графически динамический фактор по сцеплению изображается прямыми, параллельными оси абсцисс (рис. 15а). В отличие от 
динамический фактор D, определяемый формулой (49), называют динамическим фактором по тяге (или по двигателю).
, (52)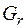
– вес полезной нагрузки.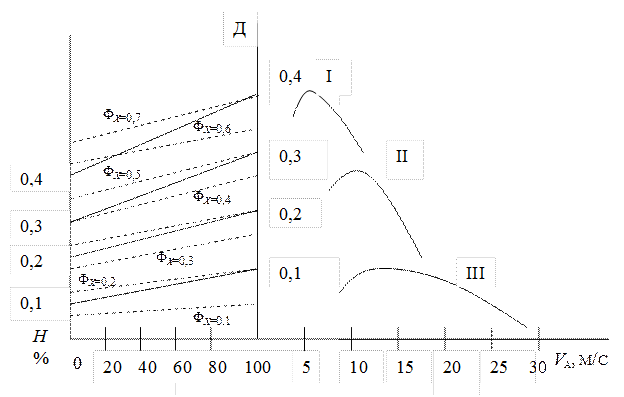
. Проведя прямые через масштабные отметки при Н = 100% и Н = 0 для различных значений D = a1, a2, …, получим номограмму масштабов для определения значений D при любом значении Н в пределах от Н = 100% до H = 0.
по оси ординат;
по оси ординат, где Zвед и Zвед0 – нормальные реакции на ведущих колесах соответственно при Н = 100% и Н = 0 %;