
|
|
Порядок построения графика ускоренийУскорение при разгоне:
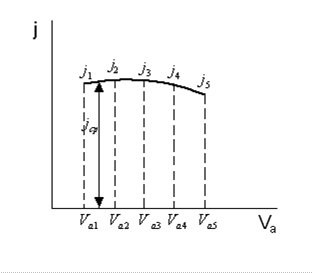
1. Наметив на графике динамической характеристики 5–6 значений скорости, находим соответствующие значения динамического фактора D и по данной формуле определяют ускорение.
2. По полученным значениям ускорения и скорости строим график зависимости ускорения от скорости.
Примерные значения
Ускорение при разгоне определяется для случая движения автомобиля по ровной горизонтальной дороге (i = 0) с твердым покрытием при максимальном использовании мощности двигателя и отсутствии буксования ведущих колес:
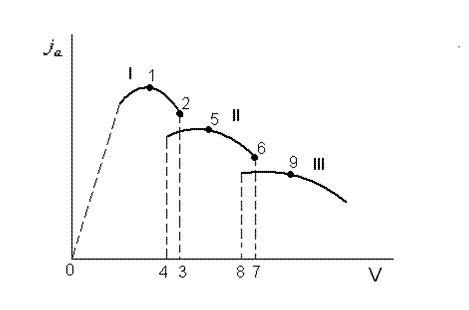
Порядок определения времени и пути разгона: 1. Кривую ускорений разбивают на интервалы для прямой передачи и читают в каждом интервале скорость.
Для повышения точности расчета интервалы скоростей берут равными 0,5-1
Общее время разгона:
2. По значениям времени разгона t строят кривую времени разгона Для скоростей Полученные точки соединяют плавной кривой.
3. Для расчета пути разгона S существует условие: в каждом интервале скоростей автомобиль движется равномерно:
По данным строим суммарную кривую S с той же точки, как и кривую t.
Задача. Определить максимальную длину подъема (
Перед подъемом автомобиль движется по участку с
Решение:
По графику находим скорость на первом участке: в начале подъема Разбиваем интервал скорости на два участка: 30…20 м/с и 20…10 м/с. Средний динамический фактор в I интервале скоростей:
Средний динамический фактор во II интервале скоростей:
Среднее замедление определяется по формуле:
Подставляем вместо значения f Среднее замедление в I интервале скоростей:
Среднее замедление во II интервале скоростей:
Путь автомобиля определяется по формуле:
Путь автомобиля в I интервале скоростей:
Путь автомобиля во II интервале скоростей:
Общая длина преодолеваемого подъема:
Определение нормальных реакций, действующих на колеса передней и задней осей
Составим уравнение моментов относительно центра тяжести автомобиля (см. рис. 12). В общем случае можно записать:
где wy – угловая скорость вращения автомобиля относительно оси у, проходящей через центр тяжести автомобиля перпендикулярно плоскости чертежа; Mk1 = Z1a1 = Z1f1rd1 – момент сопротивления качению передних колес; Mk2 = Z2a2 = Z2f2rd2 – момент сопротивления качению задних колес. Будем считать, что коэффициенты сопротивления качению и динамические радиусы одинаковы для передних и задних колес. В общем случае, если продольный профиль дороги имеет криволинейную форму, угловое ускорение wу определяется формой профиля. Если рассматривать движение автомобиля по дороге, которая может быть представлена в виде плоскости, расположенной под углом α к горизонтали, то wy = 0 и dwy / dt = 0. Обычно также пренебрегают разностью hв–hд, условно считая, что высота центра парусности равна высоте центра тяжести. Тогда, принимая во внимание, что
Кроме того, имеем:
Решая совместно равенства (60) и (61), получим:
Из равенства (34)
(62),(63) У неподвижного автомобиля на горизонтальной дороге
где G1 и G2 – вес, приходящийся на колеса соответственно передней и задней осей. Отношения нормальных реакций у движущегося автомобиля к весам, приходящимся на соответствующие оси, называют коэффициентами динамического изменения реакций
Если пренебрегать мало влияющей на эти коэффициенты силой сопротивления воздуха (для обычных негоночных автомобилей), то
Максимальные значения коэффициентов динамического изменения реакций для двухосных автомобилей с одной ведущей осью можно считать равными: mp1=0,85…0,9; mp2=1,1…1,05. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
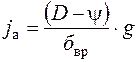
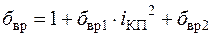
 на различных передачах.
на различных передачах.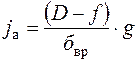
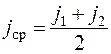
 на первой передаче, 1–3
на первой передаче, 1–3 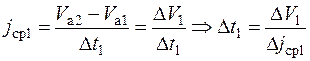
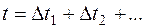


 откладывают значения
откладывают значения  ,
, 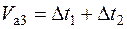
 - время переключения передач, зависящее от квалификации водителя, коробки передач и типа двигателя:
- время переключения передач, зависящее от квалификации водителя, коробки передач и типа двигателя: 
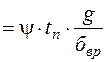
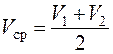
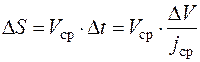
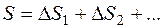
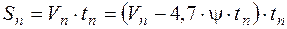
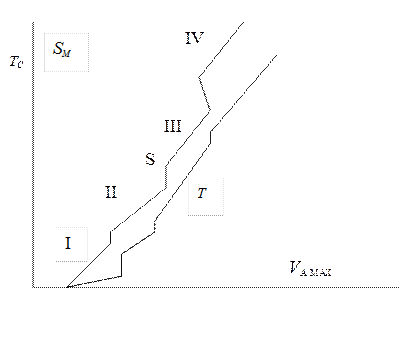
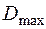 = 0,05), преодолеваемого автомобилем, динамический характер которого
= 0,05), преодолеваемого автомобилем, динамический характер которого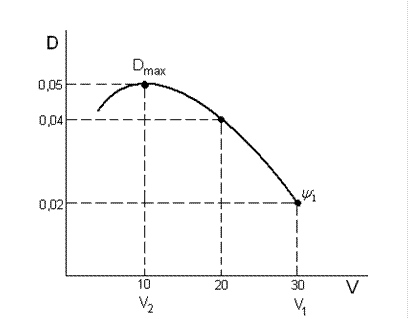
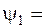 0,02 и
0,02 и  1.
1. 30 м/с и в конце подъема
30 м/с и в конце подъема  10 м/с.
10 м/с.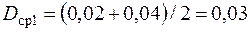
 .
.

 .
.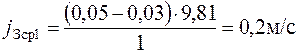
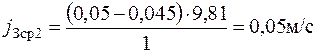
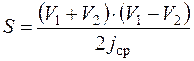
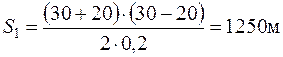
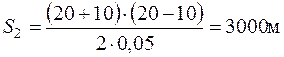
 = 4250 м
= 4250 м , (59)
, (59) , равенство (59) можно записать так:
, равенство (59) можно записать так: (60)
(60) . (61)
. (61)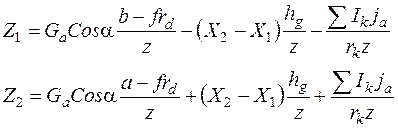
 , тогда
, тогда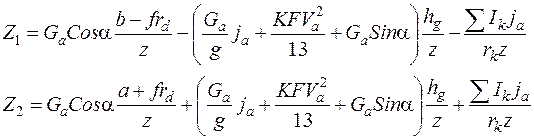
 ;
;  ,
,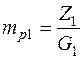

 (64)
(64) (65)
(65)