|
|
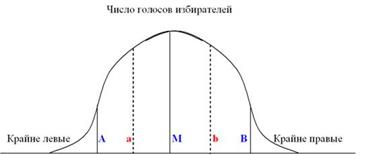
Модель взаимодействия политиков и избирателей.Модель медианного избирателя – это модель, которая характеризует тенденцию, при которой принятие решений при прямой демократии осуществляется в соответствии с интересами избирателя-центриста (лица, занимающего место в середине шкалы интересов данного общества). Решение проблем общества на основе мнения избирателя-центриста имеет как свои положительные, так и отрицательные моменты. С одной стороны, оно удерживает общество от принятия крайностей, позволяет выдержать некую середину. Но, с другой стороны, позиция центриста далеко не всегда является оптимальной. Модель медианного избирателя используется и в представительной демократии, но с некоторыми усложнениями. Дело в том, что кандидат на пост главы государства, чтобы добиться цели, должен как минимум дважды апеллировать к избирателю-центристу: сначала внутри своей партии (для прохождения процедуры выдвижения), затем к медианному избирателю среди всего населения. При этом для завоевания симпатий избирателей приходится вносить значительные коррективы в свою первоначальную программу, причем нередко отказываться от ее фундаментальных принципов. Рассмотрим в качестве примера распределение голосов избирателей в соответствии с их идеологическими предпочтениями. Отметим на горизонтальной оси позиции избирателей от крайне левых до крайне правых (рис. 14.4). В середине оси обозначим позицию медианного избирателя точкой М. Если принять, что позиции избирателей распределяются между крайностями в обществе равномерно, мы получим нормальное распределение с пиком над точкой М. Общая площадь, находящаяся под кривой, представляет 100% голосующих. Допустим, что голосующие отдают свои голоса тем, кто им ближе по своим идеологическим воззрениям.
Рис. 14.4. Распределение голосов избирателей.
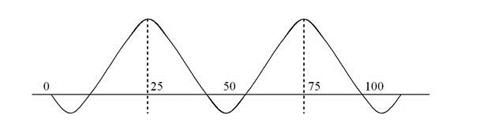
Предположим, что имеются всего два кандидата: Иванов и Сидоров. Если один из них выбирает серединную позицию (например, в точке М), то тогда он получит по крайней мере 50% голосов. Если же кандидат занимает позицию А, то он получит меньше 50% голосов. Если один кандидат занимает позицию в точке А, а другой – в точке М, то кандидат в точке А получит голоса избирателей, находящихся левее линии а, (а – срединная позиция между А и М, т.е. меньшинство голосов). Кандидат, занимающий позицию М, сможет получить голоса избирателей, находящихся правее линии а, т.е. большинство. Лучшей для кандидата будет стратегия, максимально приближенная к позиции медианного избирателя, т.к. она обеспечит ему большинство на выборах. Аналогичная ситуация сложится, если один из кандидатов будет правее другого (займет позицию в точке В). И в этом случае победа достанется тому, кто лучше отразит позицию избирателя-центриста. Проблема заключается, однако, в точном определении (идентификации) интересов и чаяний медианного избирателя. Что же произойдет, если в борьбу вступит третий кандидат? Например, один кандидат занимает позицию В, а два других – позицию М. Тогда первый получит голоса, находящиеся под кривой распределения правее линии б, а каждый из двух других – половину голосов, лежащих левее этой линии. Поэтому большинство голосов выиграет первый кандидат. Если один из двух кандидатов принял бы позицию А, то кандидат, занимающий позицию М, получил бы очень незначительный процент голосов, равный площади, находящейся по кривой распределения между а и б. Поэтому у кандидата М есть стимул выйти из сегмента АВ, тем самым поставив одного из двух других кандидатов в затруднительное положение. Процесс продвижения может долго продолжаться, но он имеет свои границы. Пока пик распределения находится в точке М, любой кандидат может повысить свои шансы, двигаясь по направлению к М. В условиях жесткого противостояния двух различных партий распределение голосов может приобрести бимодальную форму (рис. 14.5).
Рис. 14.5. Бимодальное распределение голосов.
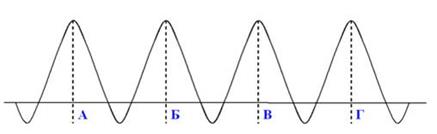
В реальной действительности бимодальное распределение может иметь как симметричную так и асимметричную форму (что встречается гораздо чаще). Наконец, в обществе, где отсутствует четкая поляризация интересов, может встретиться и полимодальное распределение голосов избирателей. Если в таком обществе действуют четыре партии, то распределение голосов может приобрести (в идеале) такую форму, которая показана на рисунке 14.6.
Рис. 14.6. Полимодальное распределение голосов.
На рисунке изображено равномерное распределение голосов между партиями, но это частный случай. Здесь также возможен асимметричный сдвиг вправо или влево.
56. Модель конкуренции групп давления за политическое влияние. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|