
|
|
КАНОНИЧЕСКОЕ РАЗЛОЖЕНИЕ МНОГОЧЛЕНА. ПРЕДСТАВЛЕНИЕ ДЕЛИТЕЛЕЙ И КРАТНЫХ МНОГОЧЛЕНОВ, ЗАДАННЫХ В КАНОНИЧЕСКОЙ ФОРМЕ.ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ Каноническое разложение многочлена Пусть P[x] = { anxn + an-1xn-1 + … + a1x + a0 | aiÎ P }. – кольцо многочленов от одной переменной с коэффициентами из поля Р. По теореме (Теорема 6.1.) всякий многочлен из кольца P [x] степени n (n ¹0) может быть представлен в виде произведения неприводимых над полем P многочленов pi (x): f(x) = p1(x) × p2(x)× . . .× pl(x), pi (x) Î P[x], 1 £ i £ l (*).Но многочлены pi (x) в произведении (*)могут повторяться (быть кратными), их можно объединить в виде степеней:
Определение 7.1. Представление многочлена f(x) п-й степени ( п > 0) из P[x] в виде Замечание: неприводимые многочлены pi (x) располагают по убыванию их степеней. Пример 7.1. Многочлен f(x) = х3– 1 – приводим над полем действительных чисел R, т.к. он предствим в виде произведения f(x) = х3 – 1 = (х - 1)(х2 + х +1). Расположив многочлены по убыванию их степеней получим каноническую форму многочлена f(x) = х3– 1 = (х2 + х +1)(х - 1). Пример 7.2. Дан многочлен f(x) = (x + 1)(x + 2)(x2 + 1)(x2 + 3x+ 2)(x3 + 3) над полем действительных чисел R. Вид, в котором дан многочлен, не является представлением в виде произведения неприводимых над полем R многочленов, т.к. один из сомножителей приводим над полем R: (x2 + 3x+ 2) = (x + 1)(x + 2). Подставив разложение многочлена (x2 + 3x+ 2) в представление f(x), получим: f(x) = (x + 1)(x + 2)(x2 + 1)(x2 + 3x+ 2)(x3 + 3) = (x + 1)(x + 2)(x2 + 1)(x + 1)(x + 2) (x3 + 3) = (x + 1)2(x + 2)2(x2 + 1)(x3 + 3) - представление в виде произведения неприводимых над полем R многочленов, расположив многочлены по убыванию их степеней, получим каноническую форму многочлена f(x) = (x3 + 3) (x2 + 1) (x + 1)2(x + 2)2. Представление многочленов в канонической форме даёт возможность легко найти все делители, кратные многочленов, а также наибольший общий делитель d(x) и наименьшее общее кратное m(x) нескольких многочленов. 1. Все делители многочлена Пример 7.3. Дан многочлен f(x) = (x3 + 3) (x2 + 1) (x + 1)2(x + 2)2 над полем действительных чисел R. Найти все его делители. Делители многочлена f(x): (x3 + 3), (x2 + 1), (x + 1), (x + 2), (x + 1)2, (x + 2)2; (x3 + 3) (x2 + 1), (x3 + 3) (x + 1), (x3 + 3) (x + 2), (x3 + 3) (x + 1)2 ,(x3 + 3) (x + 2)2, (x2 + 1) (x + 1), (x2 + 1) (x + 2), (x2 + 1) (x + 1)2, (x2 + 1) (x + 2)2, (x + 1) (x + 2), (x + 1) (x + 1)2, (x + 1) (x + 2)2, (x + 2) (x + 1)2, (x + 2) (x + 2)2, (x + 1)2(x + 2)2; (x3 + 3) (x2 + 1) (x + 1), (x3 + 3) (x2 + 1) (x + 2), (x3 + 3) (x2 + 1) (x + 1)2, (x3 + 3) (x2 + 1) (x + 2)2, (x2 + 1) (x + 1) (x + 2), (x2 + 1) (x + 1) (x + 1)2, (x2 + 1) (x + 1) (x + 2)2, (x + 1) (x + 2) (x + 1)2, (x + 1) (x + 2) (x + 2)2; (x3 + 3) (x2 + 1) (x + 1) (x + 2), (x3 + 3) (x2 + 1) (x + 1) (x + 1)2, (x3 + 3) (x2 + 1) (x + 1) (x + 2)2, (x2 + 1) (x + 1) (x + 2) (x + 1)2, (x2 + 1) (x + 1) (x + 2) (x + 2)2, (x + 1) (x + 2) (x + 1)2 (x + 2)2; (x3 + 3) (x2 + 1) (x + 1) (x + 2) (x + 1)2, (x3 + 3) (x2 + 1) (x + 1) (x + 2) (x + 2)2, (x3 + 3) (x2 + 1) (x + 1) (x + 1)2 (x + 2)2., (x3 + 3) (x2 + 1) (x + 1) (x + 1)2 (x + 2)2, (x3 + 3) (x + 1) (x + 2) (x + 1)2(x + 2)2, (x2 + 1) (x + 1) (x + 2) (x + 1)2 (x + 2)2; (x3 + 3) (x2 + 1) (x + 1) (x + 2) (x + 1)2 (x + 2)2. 2. Все кратные многочлена 3. Наибольший общий делитель d(x) нескольких многочленов, заданных над полем действительных чисел R в канонической форме
……………………………..
d(x) = (f1(x), f2(x), f3(x), fn(x))=
4. Наименьшее общее кратное m(x) нескольких многочленов, заданных над полем действительных чисел R в канонической форме
……………………………..
m(x) = [f1(x), f2(x), f3(x), fn(x)]= Пример 7.3. Даны многочлены над полем действительных чисел R. f(x)=(x+1)3(x+2)2(x2+3)4, g(x)=(x+1)(x+2)3(x+3)(x-4)3(x2+3)2. Найдём их наибольший общий делитель d(x) и наименьшее общее кратное m(x). Сначала нужно записать их канонические представления так, чтобы оба многочлена содержали одни и те же множители: f(x)=(x+1)3(x+2)2(x2+3)4(x+3)0(x-4)0= (x2+3)4(x+1)3(x+2)2(x+3)0(x-4)0, g(x)=(x+1)(x+2)3(x+3)(x-4)3(x2+3)2= (x2+3)2(x+1)1(x+2)3(x+3)1(x-4)3. Тогда d(x) = (f(x), g(x))= d(x) = (f(x), g(x))= (x2+3)2(x+1)1(x+2)2(x+3)0(x-4)0, m(x) = [f (x), g(x)]= m(x) = [f (x), g(x)]= (x2+3)4(x+1)3(x+2)3(x+3)1(x-4)3. ТИПОВЫЕ ЗАДАЧИ Задача1. Найти каноническое разложение многочлена f(x) = 6 x6 – 12 x3 + 6 над полем R. Решение. f(x) = 6 x6 – 12 x3 + 6 = 6 ( x6 – 2 x3 + 1) = 6 (x3 – 1)2 = 6 ( x – 1)2 ( x2 + x + 1)2 = 6( x2 + x + 1)2( x – 1)2. Задача 2. С какой кратностью многочлен g(x) = x + 2 входит в каноническое разложение многочлена f(x) = x5 + x4 – 8 x3 – 8 x2 + 16 x + 16 над полем R ? Решение. К многочленам применим алгоритм деления с остатком. Так как многочлен g(x) – первой степени, то воспользуемся схемой Горнера ( при хо = – 2) :
Итак, f(x) = ( x + 2)2 ( x3 – 3 x2 + 4) = ( x + 2)2 ( x + 1) ( x – 2)2. Ответ: многочлен g(x) = x + 2 входит в каноническое разложение многочлена f(x) с кратностью k = 2. УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ В примерах 175 – 180данные многочлены приведите, если это возможно, к канонической форме над полем Q и над полем R . 175.f(х) = x4 – 9. 176.g(х) = x3 – 0, 001.177.h(х) =3 x2 – x – 4. 178.j(x) = x3 – x2 – 2 x + 2.179.t (х) = x3 + 5.180.s(х) = x2 + 3. В примерах 180 – 183данные выражения представьте в канонической форме над полем R : 181.( x3 – 3 x2 + 2 x) (x4 – 1) (x4 – 8 х). 182.(x2 – 1)3 (x3 + 1)2 (x2 + х + 1) (x2 – х + 1)3 . 183.(x3 – х)2 (x5 – x2 ) (x2 – 2х ) (x2 – 4)2 . 184.(x4 – 16 )2 (x3 + 4x ) (2 – х )2 (x2 + 2 х )3 . 185.Представьте многочлен f(х) = x9 – 3 x3 – 2 в канонической форме над полем Q. 186.Найдите наибольший общий делитель d(x) и наименьшее общее кратное т(х) выражений f(х) = x (x + 1)3 (x – 1)3 (x2 + 1) и g(х) = (x+1)2 (x – 1)4 (x – 3) (x2 + 1)2. В примерах 187 – 196данные пары выражений f(х) и g(х) представьте в канонической форме над полем R , а затем найдите их наибольший общий делитель d(x) и наименьшее общее кратное т(х) 187.f(х) = (x3 – 1) (x2 – 2 х + 1) и g(х) = (x2 – 1)3 . 188.f(х) = (x2 – 9) (x2 – 4 х + 3) (x – 1)2 и g(х) = (x2 – 3 х )3 (x2 – 1) . 189.f(х) = (x2 – 1) (x2 – х) (x + 1)2 и g(х) = (x4 – 1)2 (x2 – 2 х + 1) (x – 3) . 190.f(х) = (x2 – 16) (x – 5) и g(х) = (x2 + 16) (x + 5). 191.f(х) = (x3+8) (x2 + 4 х + 4) (x2 – 4) и g(х) = (x2 +2 х )2 (x2 –2 х ) (x2 +2 х +4) 192.f(х) = (9x2 –16) (4 –3 х)3 (х – x2 )3 и g(х) = (3x2+4 х)2 (x2– х)2 (9x2–24х +16) 193.f(х) = (1 + x3) (1 – x4 )2 и g(х) = (x2 + 1)3 (x3 – 1)2 . 194.f(х) = (x2 + х – 6)2 (x2+ 4х +3) (х3 + x2 )3 и g(х) = (x2 – х – 2)2 (x2 – 2 х) (x2 + 6 х + 9)2. 195.f(х) = (9 x2 – 30 х + 25)3 (9 x2 – 25) (3 x2 – 8 х + 5) и g(х) = (3 x2 – 2 х – 5)3 (x – 1) (x3 + 6 x2 + 9 х + 4). 196.f(х) = (4 + x2) (1 – x3 )2 и g(х) = (x2 – 4) (x3 + 1) . В примерах 197 – 202определите показатель кратности неприводимого над полем R множителя р(х) данного выражения f(х) . 197.р(х) = х – 2, f(х) = (x2 – 4 х + 4) (x3 – 3 x2 + х + 2 ). 198.р(х) = x2 + 1, f(х) = (4 x2 + 4)2 (x3 – 3 x2 + х – 3 ) (x6 + 1). 199.р(х) = x – 200.р1(х) = х –1, р2(х) = 3x +4, f(х) = (3x2 + x – 4) (x2 + x – 2) (x3 – x2 + х – 1). 201. р1(х) = х +1, р2(х) = x2 +2, f(х) = (5x3 + 5x2) (x3+2x2 + х) (x3 + x2 +2х + 2). 202. р(х) = x2 – х + 2, f(х) = (x4 – 2 x3+5 x2 – 2 х + 4) (x2 – х – 2)2.
ОТВЕТЫ 1.Являются: 1), 3) , 4) , 7) , 10). 2.1) 1; 2) 2; 3) 3; 4) s – 1; 5) 0. 3.a) Многочлены над полем Q: 1), 2) , 5) ; б) многочлены над полем R: 1), 2) , 3) , 4) , 5), 7); в)многочлены над полем C: 1), 2) , 3) , 4) , 6) , 7). 4. 1) 4 x5 + 4 x4 – 8 x2 – 6 x + 1 и 4 x5 – 4 x4 – 6 x3 + 4 x2 – 8 x + 5; 2) 3 x4 и 3 x4 – 4 x3 – 10 x2 + 2 x – 8. 5.1)2 x4 – 7 x3 – 5 x2 + 14 x + 8; 2) 2 x5 – 11 x4 + 5 x3 + 14 x2 – x – 3; 3) x6+ 8. 7.2x2 + 2x + 2. 8.3x3 – 4 x2 – x + 2. 9.x + 3. 10.x4 + x3 – 3 x2 – 2 x + 1. 11.3 x2 – x – 2. 12.1)q(x) = x2 – 2 x – 7. Указание: положите q(x) = а x2 + b x + c. 2) q(x) = 3 x2 – x – 1. Указание: положите q(x) = а x2 + b x + c. 20.1) Нет; 2)нет;3)да;4)нет. 21.q(x) = 4 x3 + 3 x2 + 3 x +5, r = 7. 22.q(x) = 5 x2 – 3 x – 5, r(x) = 5 x + 4. 23.q(x) = 3 x2+ 5 x – 4, r(x) =11x – 2. 24.q(x) = 2 x2+ 3 x + 11, r(x) = 25 x – 5. 25.q(x) = 26.q(x) = 4 x2 – (3 + 4 i ) x + ( – 1 + 7 i ), r = 8 – 6 i. 27.1)q(x) = 5 x2 + x – 1, r(x) = 4 x + 7; 2)q(x) = 2 x2 + x – 2, r(x) = x2 – 3 x + 5. 28.1)g (x) = x2 – x + 2; 2) 4x3 + x + 2. 29.1)10; 2)27; 3) – 3 a3 – a2 – a + 7; 4)11 – 22 i. 30.1)22; 2) 0; 3)1. 31.1)– 5 x3 + 3 x2 + 7 x + 4; 2)5 (x – 3)3 + 3 (x – 3)2 – 7 (x – 3) + 4; 3)5 (2x) 3 + 3 (2x) 2 – 7 (2x) + 4; 4)5 (3x + 1)3 + 3 (3x + 1)2 – 7 (3x + 1) + 4. 32.q(x) = 4 x2 + 7 x + 14, r = 10. 33.q(x) = 2 x4 + 5 x3 + 5 x2 + 4 x – 1, r = 7. 34.q(x) = x3 – x2 + 3 x – 3, r = 5. 35.q(x) = 16 x4 – 12 x3 + 6 x2 – 4 x + 2, r = 1. 36.q(x) = 2 x4– 6 x3+ 13 x2– 39 x +109, r(x) = – 327. 37.q(x) = 4 x3– 3 x2+ x–1, r= 3. 38.q(x) = 40.q(x) = 4 x3 – 4 x2 + x , r = – 2. 41.q(x) = 3 x3 – 8 x2 + 16 x – 33, r = 67. 42.q(x) = 4 x3 + 3 x2 + 9 x + 17, r = 0. 43.q(x) = x3 + x2 + x + 1, r = 0. 44.197. 45.136. 46.7 – 3 i. 47. –1 – 44 i. 48.1)f (1) = 2, f (– 2) = 107, f (–1) = 0; 2)f (0) = – 3, f (1) = – 3, f (2) = 165, f (3) = 1515. 49.q(x) = 2 x3 – 4x2 + 8 x –19, r = 43 и f (3) = 158. 50.q(x) = 3 x3 – 9x2 + 28 x – 92, r = 276 и j (2) = 36. 51.q(x) = 3x2 + x +2, r = – 4 и g(– 3) = – 134. 52.q(x) = 7 x4 + 4 x3 + 4x2+ 6 x + 5, r = 0 и h (– 2) = – 267. 53. 1)x0 = 2 ;2)x0 = – 2 ;3)x0 = 1.54.– 1. 55 .– 2. 56.– 3. 57.– 6. 58.Нет целых корней. 59.7. 63.(x – 1) (x + 1) (x – 5).64.(x + 1) (x – 2) (x + 3).65.(x – 1) (x – 2) (x – 3). 66.(x + 1) (x – 2) (2x – 1).67.(x – 1)2 (x – 2) (x – 3).68.(x – 2) (x2 – x + 1).69.(x – 1) (x – 3) (x2 + 2).70.(x – 1) (x + 1) (x – 2) (x + 2).71. 1) k = 3; 2) k = 2;3) k = 4; 4) k = 3;5) k = 4;6) k1= 2 и k2= 1. 72.m =– 4. 73.p = 46. 74.m =1, n = – 2. 75.a = 2, b = – 1.76.a = – 1, b = 0.77.a = – 5. 78.a = 3, b = – 4.79.f(x) = 4x4– 27x3+ 66x2– 65x + 24. 80.f(x) = x4 – 3 x3 – 6 x2 + 28 x – 24.81. 1)U(x) = – 3 x + 4, V(x) = 3 x2 + 2 x + 1; 2)U(x) = 9 x2 – 26 x – 21, V(x) = – 9 x3 + 44 x2 –39 x – 7.82. 1)f(x) = x, 2)f(x) =x2 +1. 84.d(x) = x (x – 1).85. 1)d(x) = 1; 2)d(x) = 1; 3)d(x) = x – 1.86. 1)2 x –3; 2)x2 + 1; 3)1; 4)x + 3.87.1. 88. x + 1. 89. x – 1. 90. x2 +1. 91. x2 + x +1. 92. x + 3. 93.1. 94. x2 + 1. 95. x + 1.96. x2 – 2 x + 2. 97. x3 + 1. 98. 1)x3 – x +1; 2)x2 – 1.99.U(x) = 100. 1)d(x) = 1,U(x) = a x + b = – 3 x + 4, V(x) = c2 + d x +e = 3 x2 + 2 x +1; 2)d(x) = 1,U(x) = – 108. 1) (x – 1)2 (x2 + 2); 2)x (x2 – 4).109.d(x) = x2 – 2,U(x) = – x – 1, V(x) = x + 2. 110.d(x) = x3 + 1,U(x) = – 1, V(x) = x + 1. 111.d(x) = 1,U(x) = 3 – 2 x, V(x) = 2 x2 – 3 x + 4. 112.d(x) = 1,U(x) = – x – 1, V(x) = x3 + x2 – 3 x – 2. 113.d(x) = x3 + 2,U(x) = 1 – x2, V(x) = x3 + 2 x2 – x – 1. 114.d(x) = x – 1,U(x) = 0,2, V(x) = – 0,2(3 x + 2). 115.d(x) = 1,U(x) = 0,1 (x – 3), V(x) = 0,1 (1 + 3 x – x2). 116.d(x) = 1,U(x) = 117.d(x) = x – 1,U(x) = 0,1, V(x) = 0,1 (3 – 2 x). 118.d(x) = 1,U(x) = 119.d(x) = 1,U(x) = 120.d(x) = 1,U(x) = – 121.d(x) = 3 x + 2,U(x) = 1 + x – x2, V(x) = x3 + 2 x2 – 5 x – 4. 122.d(x) = 1,U(x) = 123.d(x) = x3 + 1,U(x) = 124.d(x) = x2 – 2 x + 2,U(x) = 125, 128, 130– взаимно простые многочлены. 136.x (x – 2)2 (x + 2). 137.d(x) = x + 3, m(x) = (x +3)2 (x – 3).138. 2 x4 – 2 x3 – x2 + 15 x – 14. 139. 2 x4 – 4 x3 + x2 + x – 6.140. x4 – 3 x3 – 7 x2 + 27 x – 18. 141. 3 x6 – 4 x5 + 10 x4 – 12 x3 + 9 x2 – 18 x + 2. 144. 1)x2(x – 2)2 ; 2)x2(x – 1)2 (x – 3)3 (x + 1). 145. a) 1), 2), 4), 5), 9), 11); б) 1), 2), 5), 9), 11);в) 1), 2), 9). 146.(x – 1)(x2 – 2 x + 2). 147.(x – 1) (x – 2) (x – 3).148.(x + 1) (x – 2) (x – 3).149.(x – 1)2 (x + 1) (x – 4). 150.(x – 1) (x – 2) (x + 4).151.(x – 2) (x – 3) (x – 4).152.(x – 3) (x – 4) (x – 5). 153(x – 1)2 (x2 + x + 1). 154.(x + 1) (x + 2)2 (x + 3).155.(x + 1)(x2 – x + 2). 156.(x +2)(x2 – 2 x + 5).157.(x2 – x + 2)(x2 + x + 2). 158. 159.(x +1)(3x2 –3x+1).160.(x + 161.(x2 – 2 x + 2)(x2 + 2 x + 2).162.(x2 – 163.(x2 – x + 1)(x2 + x + 1).164.(x2 – 165.(x – 1) (x + 1) (x2 – x + 1)(x2 + x + 1).166.(x2 – 3 x + 3)(x2 + 3 x + 3). 167.(x2 + 169.f(x) =(x–1) (x +1) (x2 +1)-над Q, и R; f(x) =(x –1) (x +1) (x – i) (x + i) –над C. 170.j (x) =(x2 – 5) (x2 + 2)-над Q; j (x) =(x – j (x) =(x – 171.g (x) = (x2 + 3)(x2 – 3 x + 3)(x2 + 3 x + 3) -над Q, и R;.g (x) = 172.h (x) = (x2 – h (x) =1/16 (2 x – 173.f(x) = (x2 – 175.f (x) = (x2 + 3)(x2 – 3) -над Q, f (x) = (x2 + 3)(x – 176.g (x) = (x – 0,1)(x2 + 0,1 x + 0,01) -над Q, и над R . 177.h (x) = (3 x – 4)( x + 1) -над Q, и над R .178.j (x) = (x2 – 2)(x – 1) -над Q, j (x) = (x – 179.t (x) -над Q неприводим , t (x) = (x + 180.s (x) -неприводим над Q, и над R . 181.x2 (x – 1)2 (x – 2)2 (x + 1) (x2 + 1) (x2 + 2 x + 4). 182.(x – 1)3 (x + 1)5 (x2 – x + 1)5 (x2 + x + 1). 183.x7 (x – 1)3 (x + 1)2 (x – 2)5 (x + 2)2 (x2 + x + 1). 184.x7 (x – 2)4 (x + 2)5 (x2 + 4)6. 185.(x + 1)2 (x2 – x + 1)2 (x3 – 2). Указание: обозначьте x3 = у. 186.d(x) = (x + 1)2 (x – 1)3 (x2 + 1), m(x) = x (x + 1)3 (x – 1)4 (x2 + 1)2 (x – 3). 187.d(x) = (x – 1)3 , m(x) = (x – 1)3 (x + 1)3 (x2 + x + 1). 188.d(x) = (x – 1)(x – 3)2, m(x) = x3(x – 1)3 (x + 1) (x – 3)3 (x + 3). 189.d(x) = (x – 1)2(x + 1)2 (x2 + 1), m(x) = x (x – 1)4 (x + 1) 3 (x2 + 1)2 (x – 3). 190.d(x) = 1, m(x) = (x – 4)(x + 4) (x – 5) (x + 5) (x2 + 16). 191.d(x) = (x – 2)(x + 2)2, m(x) = x3(x + 2)4 (x – 2) (x2 – 2 x + 4) (x2 + 2 x + 4). 192.d(x) = x3 (x – 1)2(3x + 4) (3x – 4)2, m(x) = x4(x – 1)3 (3x + 4)2 (3x – 4)4. 193.d(x) = (x – 1)2(x2+ 1)2, m(x) = (x –1)2 (x + 1)3(x2+1)3 (x2 + x +1)2 (x2 – x +1). 194.d(x) = x (x + 1)2 (x – 2)2(x + 3) 3, m(x) = x6(x + 1)4 (x – 2)3 (x + 3) 4. 195.d(x) = (x – 1)(3x – 5) 3, m(x) = (x + 4)(x – 1)2 (x + 1)5 (3x – 5)9 (3x + 5). 196.d(x) = 1, m(x) = (x –1)2 (x + 1)(x – 2)(x + 2) (x2 + x +1)2 (x2 – x +1) (x2+ 4). 197.k = 3.198.k = 4.199.k = 2.200.k1 = 3, k2 = 1. 201.k1 = 4, k2 = 1. 202.k = 2. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
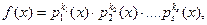 где k1 + k2 + k3 +…+ ks = n (deg f(x)).
где k1 + k2 + k3 +…+ ks = n (deg f(x)).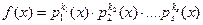 .
. заданного в каноническом видеможно записать в виде
заданного в каноническом видеможно записать в виде 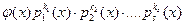 , где j(х) – любой многочлен, заданный над полем действительных чисел R.
, где j(х) – любой многочлен, заданный над полем действительных чисел R.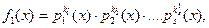
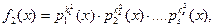
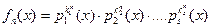 , можно записать, сообразив, что их наибольший общий делитель d(x) будет иметь в своём каноническом представлении многочлены – множители pi (x) в наименьших из степеней. Т.е.
, можно записать, сообразив, что их наибольший общий делитель d(x) будет иметь в своём каноническом представлении многочлены – множители pi (x) в наименьших из степеней. Т.е.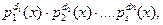 где di= min(
где di= min( 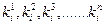 ).
).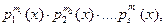 где mi= max(
где mi= max( 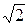 , f(х) = (x2 + 4) (x2 – 4) (x2 – 2)2 .
, f(х) = (x2 + 4) (x2 – 4) (x2 – 2)2 .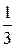 x –
x – 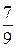 , r(x) = –
, r(x) = – 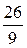 x –
x – 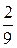 .
.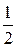 x5 –
x5 – 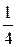 x4 –
x4 –  x3 +
x3 + 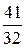 x –
x – 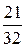 , f (–
, f (– 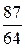 .
.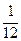 x –
x – 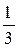 , V(x) = –
, V(x) = – 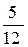 .
.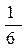 (2 x2 + 3 x), V(x) =
(2 x2 + 3 x), V(x) =  (2 x3 + 5 x2 – 6 ).
(2 x3 + 5 x2 – 6 ).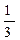 (2 – x), V(x) =
(2 – x), V(x) =  (2 x – 1), V(x) =
(2 x – 1), V(x) = 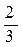 (x – 2 – 2 x2 ).
(x – 2 – 2 x2 ). (2 x – 1), V(x) =
(2 x – 1), V(x) = 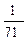 (5 x +1), V(x) =
(5 x +1), V(x) = 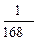 (3 x + 2), V(x) = –
(3 x + 2), V(x) = – 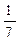 (6x2 + 9x – 28), V(x) = –
(6x2 + 9x – 28), V(x) = – 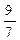 (2 x + 3).
(2 x + 3).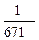 (4 – 45 x – 6 x2), V(x) =
(4 – 45 x – 6 x2), V(x) = 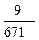 (2 x + 15).
(2 x + 15).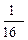 (2 x – 1 –
(2 x – 1 –  )(2 x – 1 +
)(2 x – 1 + 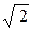 –
– 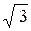 )(x+
)(x+  x + 4)(x2 +
x + 4)(x2 +  x + 1)(x2 +
x + 1)(x2 + 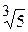 )(x2 –
)(x2 – 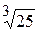 ) - над R .
) - над R .