
|
|
НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ МНОГОЧЛЕНОВ. ВЗАИМНО ПРОСТЫЕ МНОГОЧЛЕНЫ.ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ Определение 4.1. Многочлен j(x) из P[x] называется общим делителем многочленов g(x) и f(x) из P[x], если f(x) и g(x) делятся без остатка на j(x). Пример 4.1. Даны два многочлена: (x) = x4 − 4x3 + 3x2 + 2x − 6 Î R[x], g(x) = x4 − 3x3 − 4x2 + 2х + 2 Î R[x]. Общие делители этих многочленов: j1(x) = x3 − 4x2 + 2 = Î R[x], j2(x) = (x2 − 2x − 2) Î R[x], j3(x) = ( x − 1) Î R[x], j4(x) = 1 Î R[x]. (Проверьте!) Определение 4.2. Наибольшим общим делителем отличных от нуля многочленов f(x) и g(x) из P[x] называется такой многочлен d(x) из P[x], который является их общим делителем и сам делится на любой другой общий делитель этих многочленов. Пример 4.2. Для многочленов из примера 4.1. f(x) = x4 − 4x3 + 3x2 + 2x − 6 Î R[x], g(x) = x4 − 3x3 − 4x2 + 2х + 2 Î R[x] наибольшим общим делителем будет многочлен d(x) = j1(x) = x3 − 4x2 + 2 Î R[x], т. к. этот о многочлен d(x) делится на все другие их общие делители j2(x), j3(x), j4(x) . Наибольший общий делитель (НОД) обозначается символом: d(x) = (f(x), g(x)). Наибольший общий делитель существует для любых двух многочленов f(x),g(x) Î P[x] (g(x) ¹ 0). Его существование определяет алгоритм Евклида, который заключается в следующем. Делим f(x) на g(x). Остаток и частное, полученные при делении, обозначим r1(x) и q1(x). Затем, если r1(x) ¹ 0, делим g(x) на r1(x), получаем остаток r2(x) и частное q2(x) и т.д. Степени получающихся остатков r1(x), r2(x), … будут убывать. Но последовательность целых неотрицательных чисел ограничена снизу числом 0. Следовательно, процесс деления будет конечным, и мы придем к остатку rk(x), на который нацело разделится предыдущий остаток rk – 1(x). Весь процесс деления можно записать следующим образом: f(x) = g(x) × q1(x) + r1(x), deg r1(x) < deg g(x); g(x) = r1(x) × q2(x) + r2(x), deg r2(x) < deg r1(x); . . . . . . . . . . . . . . . . . . . . . . . . rk – 2 (x) = rk – 1 (x) × qk (x) + rk (x), deg rk (x) < deg rk – 1 (x); rk – 1 (x) = rk (x) × qk+1 (x). (*) Докажем, что rk (x) будет наибольшим общим делителем многочленов f(x) и g(x). 1) Покажем, что rk (x) является общим делителем данных многочленов. Обратимся к предпоследнему равенству: rk –-2 (x) = rk –-1 (x) × qk (x) + rk (x), или rk –-2 (x) = rk (x) × qk+1 (x) × qk (x) + rk (x). Его правая часть делится на rk (x). Следовательно, левая часть также делится на rk (x), т.е. rk –-2 (x) делится на rk (x). Обращаемся далее к вышележащему равенству: rk –- 3 (x) = rk –- 2 (x) × qk – 1 (x) + rk –- 1 (x). Здесь rk –- 1 (x) и rk –- 2 (x) делятся на rk (x), отсюда следует, что и сумма в правой части равенства делится на rk (x). Значит и левая часть равенства делится на rk (x), т.е. rk –- 3 (x) делится на rk (x). Продвигаясь таким образом последовательно вверх, мы получим, что многочлены f(x) и g(x) делятся на rk (x). Тем самым мы показали, что rk (x) является общим делителем данных многочленов (определение 4.1.). 2) Покажем, что rk (x) делится на любой другой общий делитель j(x) многочленов f(x) и g(x), то есть является наибольшим общим делителем этих многочленов. Обратимся к первому равенству: f(x) = g(x) × q1(x) + r1 (x). Пусть d(x) – некоторый общий делитель f(x) и g(x). Тогда по свойствам делимости разность f(x) – g(x) × q1(x) также делится на d (x), то есть левая часть равенства f(x) – g(x) × q1(x) = r1 (x) делится на d (x). Тогда и r1 (x) будет делиться на d (x). Продолжая рассуждения аналогичным образом, последовательно опускаясь по равенствам вниз, получим, что rk (x) делится на d (x). Тогда, согласно определению 4.2.rk (x) будет являться наибольшим общим делителем многочленов f(x) и g(x): d(x) = (f(x), g(x)) = rk (x). Наибольший общий делитель многочленов f(x) и g(x) является единственным с точностью до множителя - многочлена нулевой степени, или, можно сказать, с точностью до ассоциированности (определение 2.2.). Таким образом, нами доказана теорема: Теорема 4.1. /Алгоритм Эвклида/. Если для многочленов f(x),g(x) Î P[x] (g(x) ¹ 0) верна система равенств и неравенств (*),то последний, не равный нулю остаток будет наибольшим общим делителем этих многочленов. Пример 4.3. Найти наибольший общий делитель многочленов f(x) = x4 + x3 +2x2 + x + 1 и g(x) = x3 –2x2 + x –2. Решение. 1шаг.2шаг.
Запишем шаги деления в виде системы равенств и неравенств, как в (*) : f(x) = g(x) × q1(x) + r1(x), deg r1(x) < deg g(x); g(x) = r1(x) × q2(x). Согласно Теореме 4.1./Алгоритм Эвклида/ последний, не равный нулю остаток r1(x) = 7x2 + 7 будет наибольшим общим делителем d(x) этих многочленов: (f(x), g(x)) = 7x2 + 7. Поскольку делимость в кольце многочленов определена с точностью до ассоциированности (Свойство 2.11.) , то в качестве НОД можно взять не 7x2 + 7, а Ответ: будем считать, что (f(x), g(x)) = x2 + 1. Определение 4.3. Наибольший общий делитель со старшим коэффициентом 1 будем называть нормированным наибольшим общим делителем. Пример 4.4. В примере 4.2. был найден наибольший общий делитель d(x) = (f(x), g(x)) = 7x2 + 7 многочленов f(x) = x4 + x3 +2x2 + x + 1 и g(x) = x3 –2x2 + x –2. Заменив его на ассоциированный с ним многочлен d1(x) = x2 + 1, получим нормированный наибольший общий делитель этих многочленов(f(x), g(x)) = x2 + 1. Замечание.Применяя алгоритм Евклида при поиске наибольшего общего делителя двух многочленов, можно сделать следующее заключение. Наибольший общий делитель многочленов f(x) и g(x) не зависит от того, будем ли мы рассматривать f(x) и g(x) над полем P или над его расширением P’. Определение 4.4. Наибольшим общим делителем многочленов f1(x), f2(x), f3(x),… fn(x) Î P[x] называется такой многочлен d(x) Î P[x], который является их общим делителем и сам делится на любой другой общий делитель этих многочленов. Поскольку алгоритм Евклида пригоден лишь для поиска наибольшего общего делителя двух многочленов, то для поиска наибольшего общего делителя n многочленов требуется доказать следующую теорему: Теорема 4.2. (f1(x), f2(x), f3(x),… fn(x)) = ((f1(x), f2(x), f3(x),… fn-1(x)), fn(x)). Доказательство: o Введем обозначения: (f1(x), f2(x), f3(x),… fn-1(x)) = d1(x), (d1(x), fn(x)) = d(x), и докажем, что d(x) = (f1(x), f2(x), f3(x),… fn(x)). СогласноОпределению 4.4.нужно доказать два условия для d(x): 1) f1(x), f2(x), f3(x),… fn(x) 2) d(x) Докажем, что первое условие выполняется. Т.к. d(x) = (d1(x), fn(x)), то fn(x) Но т.к f1(x), f2(x), f3(x),… fn-1(x) Докажем, что второе условие выполняется. Пусть d(х) – любой другой делитель f1(x), f2(x), f3(x),… fn-1(x), fn(x). Тогда d(х) – любой другой делитель f1(x), f2(x), f3(x),… fn-1(x), а d1(x) = (f1(x), f2(x), f3(x),… fn-1(x)) Þ d1(x) Тогда d(х) –делитель fn(x) и d1(x). Но d(x) = (d1(x), fn(x))Þ d(x) 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
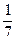 (7x2 + 7) = x2 + 1.
(7x2 + 7) = x2 + 1.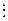 d(x);
d(x);