
|
|
Свойства операции умножения многочленов на элементы поля, над которым они заданы.Курс АЛГЕБРА 2 «Многочлены от одной переменной, ЭТГКП». (семестр 4) (68 часов = 4 часа лекций + 6 часов практич. занятий + 58 часов самостоятельной работы. Контр. работа № 2) План занятий: 1. Многочлены от одной переменной над полем Р. Операции над многочленами (сложение, вычитание, умножение). Делимость многочленов в кольце многочленов от одной переменной над полем Р. –10 часов - самостоятельная работа (стр. 1 – 14, Упражнения №№ 1 – 6, 7 – 20). Задача № 1 из контр. работы №2. 2.Деление многочленов с остатком. Деление многочлена на двучлен х – х0 . Схема Горнера. Корень многочлена. Теорема Безу. 1 час лекций, 1 час практических занятий, 10 часов - самостоятельная работа (стр. 16 – 20, Упражнения №№ 21 - 82). Задача № 2 из контр. работы №2. 3.Наибольший общий делитель многочленов. Взаимно простые многочлены. Алгоритм Эвклида. Линейное выражение НОД через многочлены. 2 часа лекций, 2 часа практических занятий, 10 часов - самостоятельная работа (стр. 25 – 29, Упражнения №№ 83 - 134). Задача № 3 из контр. работы №2. 4. Наименьшее общее кратное многочленов. Связь НОД и НОК. 10 часов - самостоятельная работа (стр. 34 – 36, Упражнения №№ 83 - 134)., Задача № 4 из контр. работы №2. 5. Неприводимые и приводимые многочлены над полем. Разложение многочлена в произведение многочленов, неприводимых над данным полем. Каноническое разложение многочлена. представление делителей и кратных многочленов, заданных в канонической форме. 1 час лекций, 2 час практических занятий, 10 часов - - самостоятельная работа (стр. 36 – 44, Упражнения №№ 135 - 141). Задача № 5 из контр. работы №2. 6.Элементы теории групп, колец и полей. 1 час практических занятий, 8 часов - самостоятельная работа, стр. упр. ; индивид. консультация). Задача № 6 из контр. работы №2.
Методические материалы к части №2 курса «АЛГЕБРА» ОГЛАВЛЕНИЕ Глава 1 Многочлены от одной переменной над полем § 1. МНОГОЧЛЕНЫ ОТ ОДНОЙ ПЕРЕМЕННОЙ НАД ПОЛЕМ Р. ОПЕРАЦИИ НАД МНОГОЧЛЕНАМИ (СЛОЖЕНИЕ, ВЫЧИТАНИЕ, УМНОЖЕНИЕ) 3 § 1. МНОГОЧЛЕНЫ ОТ ОДНОЙ ПЕРЕМЕННОЙ НАД ПОЛЕМ Р. ОПЕРАЦИИ НАД МНОГОЧЛЕНАМИ (СЛОЖЕНИЕ, ВЫЧИТАНИЕ, УМНОЖЕНИЕ) 3 ТИПОВЫЕ ЗАДАЧИ.. 8 § 2. ДЕЛИМОСТЬ МНОГОЧЛЕНОВ В КОЛЬЦЕ МНОГОЧЛЕНОВ ОТ ОДНОЙ ПЕРЕМЕННОЙ НАД ПОЛЕМ Р. 10 ТИПОВЫЕ ЗАДАЧИ.. 14 §3. ДЕЛЕНИЕ МНОГОЧЛЕНОВ С ОСТАТКОМ. ДЕЛЕНИЕ МНОГОЧЛЕНА НА ДВУЧЛЕН х – х0 . СХЕМА ГОРНЕРА. ТЕОРЕМА БЕЗУ. КОРЕНЬ МНОГОЧЛЕНА. 16 ТИПОВЫЕ ЗАДАЧИ.. 20 § 4. НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ МНОГОЧЛЕНОВ. ВЗАИМНО ПРОСТЫЕ МНОГОЧЛЕНЫ. 25 ТИПОВЫЕ ЗАДАЧИ.. 29 § 5. НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ МНОГОЧЛЕНОВ.. 34 § 6. НЕПРИВОДИМЫЕ И ПРИВОДИМЫЕ МНОГОЧЛЕНЫ НАД ПОЛЕМ. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА В ПРОИЗВЕДЕНИЕ МНОГОЧЛЕНОВ, НЕПРИВОДИМЫХ НАД ДАННЫМ ПОЛЕМ 36 ТИПОВЫЕ ЗАДАЧИ.. 40 § 7. КАНОНИЧЕСКОЕ РАЗЛОЖЕНИЕ МНОГОЧЛЕНА. ПРЕДСТАВЛЕНИЕ ДЕЛИТЕЛЕЙ И КРАТНЫХ МНОГОЧЛЕНОВ, ЗАДАННЫХ В КАНОНИЧЕСКОЙ ФОРМЕ. 42 ТИПОВЫЕ ЗАДАЧИ.. 44 ОТВЕТЫ... 45 Глава 2 Элементы теории групп, колец и полей (самостоятельно, индивид. консультация) § 1. МНОГОЧЛЕНЫ ОТ ОДНОЙ ПЕРЕМЕННОЙ НАД ПОЛЕМ Р. ОПЕРАЦИИ НАД МНОГОЧЛЕНАМИ (СЛОЖЕНИЕ, ВЫЧИТАНИЕ, УМНОЖЕНИЕ) ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
Многочлены от одной переменной над полем. Операции над многочленами. Определение 1.1. Многочленомf(x) от одной переменной х над полемP называется формальное выражение anxn + an-1xn-1 + … + a1x + a0 = f(x), где aiÎ P при 0 £ i £ n, nÎN. Элементы поляP ai при 0 £ i £ n, nÎN называются коэффициентами приx, а многочлен f(x) = anxn + an-1xn-1 + … + a1x + a0 при aiÎ P называется заданным над полем P. Пример 1.1. f(x) = 5x4 + 2x3 − 2x2 + 41x + 9 − многочлен, заданный над полем действительных чисел, а также над полем рациональных чисел, а также над кольцом целых чисел, а также над полем комплексных чисел, т.к. коэффициенты при х являются как целыми числами, так и рациональными числами, так и действительными числами, так и комплексными числами. g(x) = x5 + h(x) = x3 − ix2 + x + (i + 2) − многочлен, заданный над полем комплексных чисел, т. к. коэффициенты при х являются комплексными числами. q(x) = 2x-4 − 2x-2 + 4x0,5 + 19 − не является многочленом, т.к. выражение не соответствует требованиям (Определение 1.1.) Определение 1.2. Многочлены f(x) = anxn + an-1xn-1 + … + a1x + a0 и g(x)= bnxn + bn-1xn-1 + … + b1x + b0 называются равными, если ai= bi при 0 £ i £ max(n, m). Определение 1.3. Многочлен f(x) = 0xn +0xn-1+… +0x +0 = 0, где 0Î P, называется нулевым многочленом. Определение 1.4. Степенью ненулевого многочленаf(x) = anxn + an-1xn-1 + …+ akxk + … + a1x + a0 называется максимальное число к, для которого aк¹0. Степень нулевого многочленаравна не определена. Обозначение: deg f(x) = n, если an ¹ 0. Пример 1.2. f(x) = 5x4 + 2x3 − 2x2 + 41x + 9 − многочлен степени 4, deg f(x) = 4. g(x) = x5 + h(x) = 5 многочлен степени 0, deg h (x) = 0. Определение 1.5. Суммой двух многочленов f(x) = anxn + an-1xn-1 + … + a1x + a0 и g(x)= bmxm + bm-1xm-1 + … + b1x + b0 над полем P называется многочлен l(x) = f(x) + g(x) = сtxt + сt-1xt-1 + … + с1x + с0, где t = max(n, m), сi = ai+ bi. При этом, если n>m, то полагают bm+1 = bm = … bn = 0, а если n<m, то полагают an+1 = an = … am = 0. Разностью двух многочленов f(x) = anxn + an-1xn-1 + … + a1x + a0 и g(x)= bmxm + bm-1xm-1 + … + b1x + b0 над полем P называется многочлен h(x) = f(x) − g(x) = dtxt + dt-1xt-1 + … + d1x + a0, где t = max(n, m), dt = at − bt. При этом, если n>m, то полагают bm+1 = bm = … bn = 0, а если n<m, то полагают an+1 = an = … am = 0. Пример 1.3. Сложим многочлены из примера 1.2. f(x) + g(x) = (5x4 + 2x3 − 2x2 + 41x + 9) + (x5 + = (0x5 +5x4 + 2x3 − 2x2 + 41x + 9) + (x5 + = (0 + 1)x5 + (5 + = x5 + (5 + Обозначим множество многочленов от одной переменной х над полем Р P[x] = {anxn + an-1xn-1 + … + a1x + a0 | aiÎ P }.
Свойства операции сложения многочленов из множества P[x]. Свойство 1.1. ("f(x),g(x),h(x)Î P[x]) (f(x) +g(x)) +h(x)=f(x) +(g(x) +h(x)) − закон ассоциативности сложения многочленов. Доказательство: o Т.к. сложение многочленов сводится к сложению их коэффициентов, а сложение элементов поля P подчиняется закону ассоциативности, то и сложение многочленов подчиняется закону ассоциативности.· Свойство 1.2. ("f(x),g(x) Î P[x]) f(x) + g(x)=g(x) +f(x) − закон коммутативности сложения многочленов. Доказательство: o Т.к. сложение многочленов сводится к сложению их коэффициентов (Определение 1.5.),а сложение элементов поля P подчиняется закону коммутативности, то и сложение многочленов подчиняется закону коммутативности. ·
Свойство 1.3. ($О(x) = 0 Î P[x]) ("g(x)Î P[x]) g(x )+ 0 = g(x), − существование во множестве P[x] нейтрального элемента для операции сложения. Доказательство: o Возьмём любой многочлен g(x) = anxn + an-1xn-1 + … + a1x + a0, g(x) Î P[x]. Во множестве P[x] существует многочлен О(x) = 0xn + 0xn-1 + … + 0x + 0= 0. Прибавим к многочлену g(x) многочлен О(x): g(x) + О(x) = g(x) + 0 = (anxn + an-1xn-1 + … + a1x + a0) + (0xn + 0xn-1 + … + 0x + 0) = (an + 0)xn + (an-1+ 0)xn-1 + … + (a1+ 0)x + (a0+ 0) = anxn + an-1xn-1 + … + a1x + a0 = g(x), т.е. многочлен О(x) = 0 является нейтральным элементом для всех многочленов из P[x] · Свойство 1.4. ("f(x)Î P[x]) ($(−f(x))= (− an)xn+( − an-1)xn-1+…+( − a1)x+( − a0) Î P[x] такой, что f(x) + (−f(x)) = 0, − существование во множестве P[x] для любого элемента симметричного ему. Доказательство: o Возьмём любой многочлен f(x) = anxn + an-1xn-1 + … + a1x + a0 Î P[x]. Составим многочлен − f(x) =(− an)xn+( − an-1)xn-1+…+( − a1)x+( − a0). Он является многочленом P[x], т.к. P − поле, а в любом поле наряду с элементом aiсуществует противоположный − ai. Сложим многочлены f(x) и −f(x): f(x) + (−f(x)) = (anxn + an-1xn-1 + … + a1x + a0) + ((-an)xn+(-an-1)xn-1+…+(-a1)x+(-a0)) = (an + (-an))xn + (an-1+ (-an-1))xn-1 + … + (a1+ (-a1))x + (a0+ (-a0)) = 0xn + 0xn-1 + … + 0x + 0 = 0 = О(x) Î P[x], т.е. многочлен (-f(x)) является симметричным элементом для многочлена f(x).·
Определение 1.6. Многочлен (-f(x)) = (-an)xn+(-an-1)xn-1+…+(-a1)x+(-a0) Î P[x] называется многочленом, противоположным для многочленаf(x) = anxn + an-1xn-1 + … + a1x + a0 Î P[x] Теорема 1.1. Множество многочленов P[x] с операцией сложения многочленовявляется аддитивной группой (абелевой). o Теорема следует из свойств 1.1 – 1.4. операции сложения многочленов из множества P[x]. ·
Определение 1.7. Произведением элемента kÎP на многочлен f(x) Î P[x] называется многочлен k×f(x) = kanxn+kan-1xn-1+…+ka1x+ka0. Пример 1.4. Умножим многочлен f(x) = 5x4 + 2x3 − 2x2 + 41x + 9, заданный над полем действительных чисел, на число k = 2 из поля действительных чисел. 2f(x) = 10x4 + 4x3 − 4x2 + 82x + 18.
Свойства операции умножения многочленов на элементы поля, над которым они заданы. Свойство 1.5. ("f(x) Î P[x]) ("k, l Î P) (k l)×f(x) = k×(l×f(x)) = (k×f(x))× l).
Доказательство: o f(x) = anxn + an-1xn-1 + … + a1x + a0 Î P[x], k l Î P. (k l)×f(x) = (k l) ×(anxn + an-1xn-1 + … + a1x + a0) = ((k l)×an) xn + ((k l)×an-1) xn-1 + ...+ ((k l)×a1) x + (k l)×a0 (Определение 1.7.) = k (l×an) xn + k (l×an-1) xn-1 + ...+ k (l×a1) x + k (l×a0 )(ассоциативный закон умножения элементов поля) = k×(l an xn + l×an-1 xn-1 + ...+ l×a1 x + (l×a0 ) = k×(l×f(x)). Аналогично доказывается (k×l)×f(x) = (k×f(x))× l). · Свойство 1.6. ("f(x) Î P[x]) ("k, l Î P) (k + l)×f(x) = k×f(x) + l×f(x). Доказательство: o f(x) = anxn + an-1xn-1 + … + a1x + a0 Î P[x], k, l Î P, k + l Î P. (k + l)×f(x) = (k + l) × (anxn + an-1xn-1 + a1x + a0) = ((k + l) × an) xn + ((k + l) × an-1)xn-1 + … + ((k + l) × a1) x + ((k + l) × a0) (Определение 1.7.)= (k× an + l × an) xn + (k× an-1 + l × an-1) xn-1 + … + (k× a1 + l × a1) x + ((k + l) × a0) (дистрибутивный закон умножения элементов поля относительно их сложения)= (k× an) xn + (l × an) xn + (k× an-1) xn-1 +(l × an-1) xn-1 + … + (k× a1) x + (l × a1) x + (k × a0) + ( l × a0) (Определение 1.5.) = (k anxn + k an-1xn-1 + …+ k a1x + k a0) + (l anxn + l an-1xn-1 +… + l a1x + l a0) = k ×f(x) + l×f(x). · Свойство 1.7. ("f(x),g(x) Î P[x]) ("k Î P) k (f(x) +g(x)) = k×f(x) + k×g(x). Доказательство: o f(x) = anxn + an-1xn-1 + … + a1x + a0 Î P[x], g(x)= bmxm + bm-1xm-1 + … + b1x + b0 Î P[x], n>m, k Î P. k (f(x) +g(x)) = k ((anxn + an-1xn-1 + … + a1x + a0)+(bmxm + bm-1xm-1 + … + b1x + b0)) = k ((anxn + an-1xn-1 + … + a1x + a0)+(0xn + 0xn-1 … +bmxm + bm-1xm-1 + … + b1x + b0)) = k ((an + 0)xn + (an-1 + 0)xn-1 + …+ (am + bm)xm +… + (a1 + b1)x + (a0 + b0)) (Определение 1.5.)= k(an + 0)xn + k (an-1 + 0)xn-1 + … + k (a1 + b1)x + k (a0 + b0) (Определение 1.7.) =(k an + k 0)xn + (k an-1 + k 0) xn-1 + … +(k a1 + k b1) x +(k a0 + k b0) (дистрибутивный закон умножения элементов поля относительно их сложения) = (k an xn + k 0 xn) + (k an-1 xn-1 + k 0 xn-1 ) + … +(k a1 x + k b1 x) +(k a0 + k b0) (Свойство 1.6.)= (k an xn + k an-1 xn-1 + … + k a1 x + k a0) + (k 0 xn + k 0 xn-1 + … + k bm xm + …+ k b1 x + k b0) = k (an xn + an-1 xn-1 + … + a1 x + a0) + k (0 xn + 0 xn-1 + … + bm xm + …+ b1 x + b0) = k×f(x) + k×g(x). · Свойство 1.8. ("f(x) Î P[x]) (1× Î P) 1×f(x) = f(x). Доказательство: o f(x) = anxn + an-1xn-1 + … + a1x + a0 Î P[x], 1 Î P. 1××f(x) = 1× (anxn + an-1xn-1 + … + a1x + a0) = 1× anxn + 1× an-1xn-1 + … + 1× a1x + 1× a0 (Определение 1.7.)= anxn + an-1xn-1 + … + a1x + a0 ( т.к 1 – нейтральный элемент операции умножения элементов поля) = f(x). · Определение 1.8. Произведением двух многочленов f(x) = anxn + an-1xn-1 + … + a1x + a0 и g(x)= bnxm + bn-1xm-1 + … + b1x + b0 называется многочлен l(x) = = f(x) ∙ g(x) = сtxt + сt-1xt-1 + … + с1x + с0, где ск = åaibj, к = i + j, t = n + m. Пример 1.5. Умножим f(x) = x4 + 2x3 − x2 + 4x + 1 на g(x) = x3 − 2x2 + 3x − 1. f(x) ∙ g(x) = (x4 + 2x3 − x2 + 4x + 1) ∙ (x3 − 2x2 + 3x − 1) = x4 ∙ x3 + x4 ∙ (− 2x2) + x4 ∙ 3x + x4 ∙ (− 1) + 2x3 ∙ x3 + 2x3 ∙ (− 2x2) + 2x3 ∙ 3x + 2x3 ∙ (−1) + (− x2) ∙ x3 + (− x2) ∙ (− 2x2) + (− x2) ∙ 3x + (− x2) ∙ (− 1) + 4x ∙ x3 + 4x ∙ (− 2x2) + 4x ∙ 3 x + 4x ∙ (− 1) + 1 ∙ x3 + 1 ∙ (− 2x2) + 1 ∙ 3 x + 1 ∙ (− 1) = x7 − 2x6 + 3х5 − x4 + 2x6 − 4х5 + 6 x4 − 2x3 − x5 + 2 x4 − 3x3 + x2 +4x4 − 8 x3 + 12х2 − 4x + x3 − 2x2 + 3x − 1 = x7 − 2x5 + 11x4 − 8x3 + 13x2 − x − 1. Теорема 1.2. Множество многочленов P[x] с операциями сложения элементов и умножения на элемент поля P является векторным пространством над полем P. o Теорема следует из свойств 1.1. – 1.4. операции сложения многочленов из множества P[x] и из свойств 1.5. – 1.8. операции умножения многочленов из множества P[x] на элементы множества P. · Определение 1.9. Многочлен вида акxк называется одночленом. Применяя к одночленам anxn, an-1xn-1,…,a1x, a0 операцию сложения многочленов (Определение 1.5.), видим, что многочлен f(x) =anxn + an-1xn-1 +…+ a1x + a0 является суммой этих одночленов (Определение 1.1.). Аналогично, при умножении одночлена х на себя к раз, т.е. х × х ×…× х (к раз), получим одночлен xк (Определение 1.8.). Умножив одночлен xк на коэффициент ак, получим одночлен акxк (Определение 1.7.).
Свойства операции умножения многочленов из множества P[x]. Свойство 1.9. ("f(x),g(x),h(x)Î P[x]) (f(x) × g(x)) × h(x) = f(x) × (g(x) × h(x)) − закон ассоциативности умножения многочленов. Доказательство: o Т.к. умножение многочленов сводится к умножению их коэффициентов (Определение 1.8.),а умножение элементов поля P подчиняется закону ассоциативности, то и умножение многочленов подчиняется закону ассоциативности. · Свойство 1.10. ("f(x),g(x) Î P[x]) f(x) × g(x)=g(x) × f(x) − закон коммутативности умножения многочленов. Доказательство: o Т.к. умножение многочленов сводится к умножению их коэффициентов (Определение 1.8.), а умножение элементов поля P подчиняется закону коммутативности, то и умножение многочленов подчиняется закону коммутативности. · Свойство 1.11. ($e(x) = 1 Î P[x]) ("g(x)Î P[x]) g(x) × 1= 1× g(x) − существование во множестве P[x] нейтрального элемента для операции умножения. Доказательство: o Возьмём из P[x] любой многочлен g(x) = anxn + an-1xn-1 + … + a1x + a0, g(x) Î P[x]. Во множестве P[x] существует многочлен е(x) = 0xn + 0xn-1 + … + 0x + 1 = 1. (Свойство 1.11). Умножим многочлен g(x) намногочлен е(x): g(x) × е(x) = g(x) × 1 = (anxn + an-1xn-1 + … + a1x + a0) × 1= (an × 1)xn + (an-1 × 1)xn-1 + …+ (a1 × 1)x + (a0 × 1) = anxn + an-1xn-1 + … + a1x + a0 = g(x), т.е. многочлен е(x) = 1 является нейтральным элементом при умножении многочленов из P[x]· Свойство 1.12. ("f(x),g(x),h(x)ÎK[x]) f(x) × (g(x) + h(x))= f(x) × g(x) + f(x) × h(x) − закон дистрибутивности умножения многочленов относительно их сложения. Доказательство: o Т.к. умножение многочленов сводится к умножению их коэффициентов (Определение 1.8.), сложение многочленов сводится к сложению их коэффициентов (Определение 1.5.), а операция умножения элементов поля относительно их сложения подчиняется закону дистрибутивности, то и умножение многочленов относительно их сложения подчиняется закону дистрибутивности. · Теорема 1.3. Множество многочленов P[x] с операциями сложения и умножения элементов является кольцом. o Теорема следует из свойств 1.1 – 1.4. операции сложения многочленов из множества P[x] и из свойства 1.12. операции умножения многочленов из множества P[x].· Определение 1.10. Множество P[x]многочленов от одной переменной, заданных над полем P, с определёнными в нём операциями сложения (Определение 1.5.) и умножения (Определение 1.7.) называется кольцом многочленов от одной переменной над полемP. ТИПОВЫЕ ЗАДАЧИ Задача 1. Установить, является ли выражение 5х2 + 2х + 3 многочленом от одной переменной хнад полем действительных чисел R. Решение: Т.к. выражение 5х2 + 2х + 3 имеет вид a2x2 + a1x + a0, где a2 = 5ÎR, a1 = 2ÎR, a0 = 3ÎR, то выражение 5х2 + 2х + 3 является многочленом от одной переменной х над полем действительных чисел R(Определение 1.1.). Задача 2. Установить, является ли выражение Решение: Т.к. выражение й переменной х над полем рациональных чисел Q(Определение 1.1.). Задача 3. Определить степень многочлена f(х) = 1 – 3x – 4x2 + 5х5 над полем R : Решение: Степень многочлена f(х) = 1 – 3x – 4x2 + 5х5 над полем R равна 5 (Определение 1.4.). Задача 4.: Найти сумму и разность многочленов f(х) = 4 х2 + 3 х + 5 и g(х) = 5х5 – 4x2– 3x + 5. Решение: f(х) + g(х) = (4 х2 + 3 х – 15) + (5х5 – 6x2– 3x + 5) = 5х5 – 2x2– 10. f(х) – g(х) = (4 х2 + 3 х – 15) – (5х5 – 6x2– 3x + 5) = – 5х5 + 10x2+ 6х – 20. Задача 5.: Найти 2f(х) – 3g(х) многочленов f(х) = 2х4+ 3х3 + 3х2 + х – 5 и g(х) = х5 – x2– 3x + 5. Решение: 2f(х) – 3g(х) = 2(2х4+ 3х3 + 3х2 + х – 5) – 3(х5 – x2– 3x + 5) = (4х4+ 6х3 + 6х2 + 2х – 10) – (3х5 – 3x2– 9x + 15) = – 3х5 + 4х4+ 6х3 + 9х2 + 11х – 25. Задача 6.: Найти произведение многочленов f(х) = 3х3 + 5х + 1 и g(х) = х4 – x + 1. Решение: f(х) × g(х) = (3х3 + 5х + 1) × (х4 – x + 1) = х7 – х4+ х3 + 5х5 –5х2 + 5х + х4 – х + 1 = х7 + 5х5 + х3 –5х2 + 4х + 1. УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ 1.Установите, являются ли следующие выражения многочленами от одной переменной х над полем R : 1)х2 + 3; 2)2 5)(х2 + 3) (1 – x ); 6)х – 2 + х – 1 + 1;7) 10)4 х2 + a х – 2.Определите степень многочлена f(х) над полем R : 1)f(х) = 3 – 5 x; 2)f(х) = 1 – 3 x – 4 x2; 3)f(х) = 0 + 0 × x – 0 × x2+ 2 x3; 4)f(х) = a0 + a1 x + a2 x2+ … + as – 1 xs – 1 + 0 × xs (ai Î R, ai ¹ 0 );.5)f(х) = 3.Можно ли утверждать, что данные выражения являются многочленами а)над полем Q: 1)x2+ 4;2) б)над полем R: 1)x2 + 9; 2)x2 – 9; 3)x2 + 2; 4)x2 + в)над полем C: 1)x3 – 5) 4.Найдите сумму и разность многочленов f(х) и g(х), если : 1)f(х) = 4 х5– 3 х3 – 2 х2 – 7 х + 3, g(х) = 4 х4+ 3 х3 – 6 х2 + х – 2; 2) f(х) = 3 х4– 2 х3 – 5 х2 + х – 4, g(х) = 2 х3+ 5 х2 – х + 4. 5.Найдите произведение многочленов f(х) и g(х), если : 1) f(х) = х2 – 3 х – 2, g(х) = 2 х2 – х – 4. 2)f(х) = 2 х3 – 3 х2 – х + 1, g(х) = х2 – 4 х – 3; 3)f(х) = х4 – 2 х2 + 4, g(х) = х2 + 2. 6.Найдите - 2f(х) + g(х) многочленов f(х) = х4 – 3х3 + х2 + 2х – 1 и g(х) = 2х5 – x4– x + 2. § 2. ДЕЛИМОСТЬ МНОГОЧЛЕНОВ В КОЛЬЦЕ МНОГОЧЛЕНОВ ОТ ОДНОЙ ПЕРЕМЕННОЙ НАД ПОЛЕМ Р. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ Определение 2.1. Многочлен f(x) из кольца многочленов P[x] делится на многочлен g(x) из того же кольца P[x], если в этом кольце существует многочлен q(x) такой, что f(x) = g(x) × q(x). В этом случае многочлен f(x) называетсяделимым, многочлен g(x) называется делителем,многочлен q(x) называетсячастным.
Пример 2.1. Возьмём в поле R многочлен второй степени f(x) = x2 – 4. Т.к. f(x) = (x – 2) (x + 2), то многочлен f(x) делится на многочлен (x – 2) и многочлен f(x) делится на многочлен (x + 2). Деление в кольце многочленов P[x] не всегда выполнимо. Так, если взять многочлены f(x) = x + 2, g(x) = x2 + 4 и предположить, что f(x) делится на g(x), то в кольце многочленов P[x] должен существовать многочлен q(x) такой, что x + 2 = (x2 + 4) × q(x)(Определение 2.1.). Но это равенство невозможно. Следовательно, f(x) не делится на g(x). Символ Пример 2.2. а) (x2 – 4) что x2 – 4 = (x – 2) × (x + 2). б) (x2 – 4) что x2 – 4 = (x + 2) × (x – 2). Свойства делимости многочленов из кольца многочленов P[x]. Свойство 2.1.Если f(x), g(x), h(x) – многочлены из P[x], h(x) ¹ 0, то из f(x) × h(x) = g(x) × h(x) следует f(x) = g(x) (закон сокращения). o Пусть f(x) × h(x) = g(x) × h(x) для f(x), g(x), h(x) Î P[x]. Разделим обе части равенства на h(x): левая часть: f(x) × h(x) = h(x) × f(x) Þ f(x) × h(x) правая часть: g(x) × h(x) = h(x) × g(x) Þ g(x) × h(x) Свойство 2.2.Обратимыми элементами кольца P[x]являются многочлены нулевой степени -обратимые элементы поля P. o Действительно, обратимые элементы поля P: ("аÎ P)(а ¹ 0)($ а-1Î P), такие, что а× а-1 = 1 Î P), обратимые элементы кольца P[x]: ("f(x) = а ÎP[x])(а ¹ 0)($ f(x) = а-1ÎP[x]), такие, что (а× а-1 = 1 Î P[x]). · Определение 2.2. Два многочлена, отличающиеся множителем - многочленом нулевой степени, называются ассоциированными. Пример 2.3. Возьмём в кольце многочленов P[x] многочлен второй степени f(x) = x2 – 4. f(x) = x2 – 4 = 5 × f(x) = x2 – 4 = 7 × f(x) = x2 – 4 = (-2) × ( Т. е., согласно определению 2.2.,многочлены f(x) = x2 – 4, f1(x) = ( Свойство 2.3. 0 делится на любой многочлен f(x) Î P[x]. Доказательство: o Возьмём любой многочлен f(x)Î P[x]. 0 = f(x) × 0 Þ 0 Свойство 2.4.Всякий многочлен f(x) из кольца многочленов P[x] делится на любой обратимый элемент из P (из P[x]). Доказательство: o Возьмём любой многочлен f(x)Î P[x]. f(x) = f(x)×1(1Î P) (Свойство 1.11.)= f(x)×(a×a-1)(aÎ P) (Существование обратного элемента для любого ненулевого элемента поля) = (a×a-1)×f(x) (Свойство 1.10.) = a×(a-1×f(x))(Свойство 1.9.), где (a-1×f(x)) Î P[x] Þ f(x) Свойство 2.5.Всякий многочлен f(x) из кольца многочленов P[x] делится на любой ассоциированный с ним многочлен. Доказательство: o Возьмём любой многочлен f(x)Î P[x]. f(x) = f(x)×1(1Î P) (Свойство 1.11.) = f(x)×(a×a-1)(aÎ P) (Существование обратного элемента для любого ненулевого элемента поля) = (a×a-1)×f(x) (Свойство 1.10.) = (a-1×a)×f(x) (Свойство коммутативности умножения элементов поля) = a-1×(a×f(x)) (Свойство 1.9.) = (a×f(x))× a-1(Свойство 1.10.), где a-1Î P[x] Þ f(x) Свойство 2.6.Отношение делимости в P[x] рефлексивно (всякий многочлен f(x) делится на самого себя). Доказательство: o Возьмём любой многочлен f(x)Î P[x]. f(x) = f(x) 1, причём 1 = e(x) Î P[x] (Свойство 1.11.)Следовательно, f(x) Свойство 2.7.Отношение делимости в P[x]транзитивно (если многочлен f(x) делится на g(x), а g(x) делится на h(x), то f(x) делится на h(x)). Доказательство: o f(x) g(x) Подставим второе равенство в первое: f(x) = g(x)× q1(x) =(h (x)× q2(x)) × q1(x) = h (x)× (q2(x) × q1(x)) (Свойство 1.9. Закон ассоциативности умножения многочленов) = h (x) × q3(x), где q3(x) Î P[x]. · Свойство 2.8.Если f(x) и g(x) – многочлены из P[x], f(x) делится на g(x), a g(x) делится на f(x), то f(x) и g(x) отличаются друг от друга лишь множителем - многочленом нулевой степени: f(x) = c × g(x), где c Î P, (c отлично от нуля), т.е.оба они ассоциированы друг с другом. Доказательство: of(x), g(x) Î P[x], f(x) f(x) = g(x) × q1(x) (1). g(x) = f(x)× q2(x)(2), q1(x) Î P[x], q2(x) Î P[x]. Подставим второе равенство в первое: f(x) =( f(x)× q2(x))× q1(x), f(x) = f(x)× (q2(x))× q1(x)) (Свойство 1.9.) Очевидно, q2(x))× q1(x) = 1 = e(x) Î P[x]. С другой стороны, 1 Î P. Откуда следует, что многочлены q2(x)), q1(x) могут быть только многочленами нулевой степени, т.е. взаимно обратными элементами поля Р, и f(x) и g(x) отличаются друг от друга лишь множителем - многочленом нулевой степени: f(x) = c × g(x), где c Î P ( c отлично от нуля). g(x) = c-1 × f(x), где c-1 Î P, т.к. c отлично от нуля. · Свойство 2.9. Если многочлены f1(x) и f2(x) из P[x] делятся на g(x) из P[x], то их сумма f1(x) + f2(x) и разность f1(x) – f2(x) делятся на g(x). Доказательство: o f1(x) f2(x) Сложим равенства: f1(x)+ f2(x) = g(x)× q1(x)+ g(x)× q2(x) = g(x)×(q1(x) + q2(x))= g(x)×q3(x), где q3(x) Î P[x], Þ f1(x)+ f2(x) 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
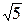 x4 +
x4 + 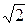 x3 − 2x2 + x + 3 − многочлен над полем действительных чисел, а также над полем комплексных чисел.
x3 − 2x2 + x + 3 − многочлен над полем действительных чисел, а также над полем комплексных чисел.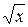 + 3; 3)
+ 3; 3) 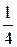 х + 3;8)
х + 3;8) 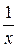 ; 9)
; 9) 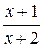 ;
; (a = const, a Î R);11)4 х2 + 3 t2 + 5; 12)х2 + х + i .
(a = const, a Î R);11)4 х2 + 3 t2 + 5; 12)х2 + х + i .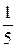 .
.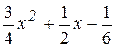 ;3)3 х2 + х +
;3)3 х2 + х +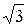 x +
x + 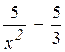 ; 7)
; 7) 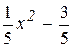 ; 8)x +
; 8)x + 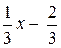 ; 4)x2 +
; 4)x2 +  ;
;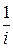 ; 7)х2 + х + 3;8)3 х – 2 + 2 х – 1 + 4?
; 7)х2 + х + 3;8)3 х – 2 + 2 х – 1 + 4? означает: « делится без остатка».
означает: « делится без остатка».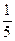 (x2 – 4) = 5 ×(
(x2 – 4) = 5 ×(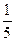 x2 –
x2 – 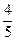 ) = 5 f1(x),
) = 5 f1(x),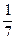 ×(x2 – 4) = 7 ×(
×(x2 – 4) = 7 ×(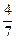 ) = 7 f2(x),
) = 7 f2(x),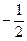 )×(x2 – 4) = (
)×(x2 – 4) = (