|
|
Теорема 4.3. (о линейном представлении НОД двух многочленов).Если d(x) – наибольший общий делитель многочленов f(x) и g(x) из P[x], то в том же кольце P[x] найдутся многочлены U(x) и V(x) такие, что f(x) × U(x) + g(x) × V(x) = d(x).
Заметим, что Теорема 4.3.(о линейном представлении НОД двух многочленов) распространяется на n – ое количество многочленов, т.е. Теорема 4.4. (о линейном представлении НОД многочленов) Если d(x) – наибольший общий делитель многочленов f1(x), f2(x), f3(x),…fn-1(x), fn(x) Î P[x], то в том же кольце P[x] найдутся многочлены V1(x), V2(x), V3(x)… Vn(x) такие, что f1(x) × V1(x) + f2(x) × V2(x)+ f3(x) × V3(x) + fn(x) × Vn(x) = d(x). Определение 4.5. Многочлены f1(x), f2(x), f3(x),…fn-1(x), fn(x) называются взаимно простыми, если их наибольший общий делитель равен единице, т.е. (f1(x), f2(x), f3(x),… fn-1(x), fn(x)) = 1. Пример 4.4. Для многочленов f(x) = 2x − 1 Î R[x], g(x) = х + 2 Î R[x] их НОД d(x) = (f(x), g(x)) = 1, т.е. многочлены f(x) и g(x) являются взаимно простыми.
Свойства взаимно простых многочленов из кольца многочленов P[x]. Свойство 4.1.Многочлены f1(x), f2(x), f3(x),…fn-1(x), fn(x) взаимно простые тогда и только тогда, когда найдутся в том же кольце многочленов P[x] многочлены U1(x), U2(x), U3(x)… Un(x) такие, что f1(x) × U1(x) + f2(x) × U2(x)+ f3(x) × U3(x) + ….+ fn(x) × Un(x) = 1. Свойство 4.2.Если (f1(x), f2(x), f3(x),…fn(x)) = d(x), то Свойство 4.3.Если (f(x) × j(x)) o(f(x), h(х)) = 1 Þ в кольце P[x] найдутся многочлены U(x) и V(x) такие, что f(x) × U(x) + h(х) × V(x) = 1. Свойство 4.4.Если многочлен j(x) взаимно прост с каждым из многочленов f1(x), f2(x), f3(x),…fn(x), то j(x) взаимно прост с произведением многочленов f1(x) × f2(x) × f3(x) × … × fn(x). Пример 4.5. Найдём наибольший общий делитель многочленов f1(x) = x3 +x2 –x –1, f2(x) = x3 –x2 –x +1, f3(x) = x3 –x. По Теореме 4.2. (f1(x), f2(x), f3(x)) =((f1(x), f2(x)), f3(x)). Т.е. для того, чтобы найти НОД d(x ) трёх многочленов f1(x), f2(x), f3(x), необходимо найти НОД d1(x ) двух многочленов f1(x), f2(x), а затем нужно найти НОД d2(x ) двух многочленов d1(x ) и f3(x). При этом d2(x ) = d(x) (Теорема 4.2). Итак, (f1(x), f2(x)) = d1(x ) = x2 –1, а (d1(x ), f3(x)) = d(x ) = x2 –1 = (f1(x), f2(x), f3(x)). ТИПОВЫЕ ЗАДАЧИ Задача1. Найти наибольший общий делитель многочленов f(x) = x4 + 3x3 –x2 –4x –3 и g(x) = 3x3 + 10x2 + 2x –3. Решение. Применяя алгоритм Евклида в данном примере, мы будем вынуждены проводить вычисления с дробными коэффициентами многочленов, что, естественно, затрудняет и замедляет процесс поиска наибольшего общего делителя данных многочленов. Но так как НОД определяется с точностью до множителя нулевой степени, в некоторых случаях можно избежать дробных коэффициентов. Будем умножать делимое, делитель, остаток на любое не равное нулю число, т.е. заменять многочлены на ассоциированные с ними, но так, чтобы равенство f(x) = g(x) × q(x) + r(x) (Теорема 3.1.) не нарушалось. Делим f(x) на g(x) согласно алгоритму Евклида, предварительно умножив f(x) на 3. 1шаг.
Наибольший общий делитель многочленов f(x) = x4 + 3x3 –x2 –4x –3 и g(x) = 3x3 + 10x2 + 2x –3 – это последний, не равный нулю остаток r2(x) = 9x + 27, или ассоциированный с ним, более простой многочлен Задача2. Для многочленов из задачи 1 над полем рациональных чисел найти многочлены U(x) и V(x) над тем же полем, чтобы имело место равенство f(x) × U(x) + g(x) × V(x) = d(x), где d(x) = ( f(x), g(x) ). Решение. Запишем результаты делений: 1шаг. 3f(x) = g(x) × q1(x) + r1(x); 2шаг. g(x) = (– 3шаг. – d(x) = (f(x), g(x)) = x + 3 = d(x) = (f(x), g(x)) = x + 3 = d(x) = (f(x), g(x)) = x + 3 = Итак: f(x) × [ Т. е. функции U(x) и V(x) найдены: U(x) = Тогда d(x) = x + 3 = f(x) × ( Осталось проверить полученное равенство: f(x) × (
УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ 83.Даны многочлены f(x) = х (х – 1 )3 и g(x) = х4 (х – 1)2 (х + 1). 1)Составьте 3 – 4 многочлена, являющихся делителями многочлена f(x) ; 2)Составьте 3 – 4 многочлена, являющихся делителями многочлена g(x) ; 3)Составьте 2 – 3 многочлена, являющихся общими делителями многочленов f(x) и g(x); 4)Составьте многочлен,являющийся наибольшим общим делителем многочленов f(x) и g(x) и убедитесь в том, он удовлетворяет всем требованиям, содержащимся в определении наибольшего общего делителя многочленов. 84.Каков наибольшийобщийделитель многочленов f(x) = x3 – 4 x, g(x) = х (х – 2)2 и h(х) = x3 – 2 x2 ? 85.С помощью алгоритма Евклида найдите нормированный наибольшийобщийделитель d(x) многочленов : 1)f(х) = x4 + x3 – 3 x2 + 4 x – 5 и g(х) = x3 – 2 x2 + 2 x – 2 ; 2)f(х) = x4 – 6 x3 + 24 x – 6 и g(х) = x3 – 5 x2 – 4 x + 17 ; 3)f(х) = – x5 – 2 x4 + x3 + 4 x2 + x – 3 и g(х) = – x4 – x3 + x2 + 2 x – 1 .
86.С помощью алгоритма Евклида найдите наибольшийобщийделитель d(x) многочленов f(x) и g(x), применяя при этом два варианта вычислений: I– обычное деление многочленов « уголком »; II –используя для удобства деления предварительное умножение делимого на некоторое постоянное число и сокращение остатков на постоянное число. Сравните результаты. 1)f(х) = 2 x3 – 5 x2 – x + 6, g(х) = 6 x2 – 5 x – 6 ; 2)f(х) = x4 – x3 – x2 – x – 2, g(х) = 2 x3 – 3 x2 + 2 x – 3 ; 3)f(х) = x3 – 3 x2 – x – 1, g(х) = 3 x2 – 2 x + 1 ; 4)f(х) = x4 + 3 x3 – x2 – 4 x – 3, g(х) = 3 x3 – 10 x2 + 2 x – 3 .
В примерах 87 – 97с помощью алгоритма Евклида найдите нормированный наибольшийобщийделитель d(x) многочленов f(x) и g(x) . 87.f(х) = x2 – 1 , g(х) = x2 + 1 . 88.f(х) = x3 + 1 , g(х) = x2 – 1 . 89.f(х) = x3 – 3 x2 – 2 x + 4 , g(х) = x2 – 5 x + 4 . 90.f(х) = x4 + x3 + 2 x2 + x + 1 , g(х) = x3 – 2 x2 + x – 2 . 91.f(х) = x5 + x4 – x3 – 3 x2 – 3 x – 1 , g(х) = x4 – 2 x3 – x2 – 2 x + 1 . 92.f(х) = x5 + 3 x4 – 12 x3 – 52 x2 – 52 x – 12, g(х) = x4 + 3 x3 – 6 x2 – 22 x – 12. 93.f(х) = x4 – 4 x3 + 1 , g(х) = x3 – 3 x2 + 1 . 94.f(х) = x5 + x4 – x3 – 2 x – 1 , g(х) = 3 x4 + 2 x3 + x2 + 2 x – 2. 95.f(х) = x4 + x3 – 3 x2 – 4 x – 1 , g(х) = x3 + x2 – x – 1 . 96.f(х) = x5 – 2 x4 + x3 + 7 x2 – 12 x + 10 , g(х) = 3 x4 – 6 x3 + 5 x2 +2 x – 2. 97.f(х) = x6 – 7 x4 + 8 x3 – 7 x + 7 , g(х) = 3 x5 – 7 x3 + 3 x2 – 7. 98.Найдите наибольшийобщийделитель d(x) многочленов f(x), g(x) и h(х) : 1)f(х) = x6 +2 x4 – 4 x3 – 3 x2 + 8 x – 5 , g(х) = x5+ x2– x +1, h(х) = x4 + x3 – x2 +1. 2)f(х) = x4 – 3 x3 + x2 + 3 x – 2 , g(х) = x4 – 5 x2 + 4, h(х) = x3 + 3 x2 – х – 3 . 99.Даны многочлены f(x) = (х + 1)(х – 3) и g(x) = х (х – 1) . С помощью метода неопределённых коэффициентов найдите многочлены U(x) и V(x), удовлетворяющие равенству: f(х) × U(x) + g(x) × V(x) = 1 . 100.Используя алгоритм Евклида , найдите наибольшийобщийделитель d(x) многочленов f(x) и g(x) , а затем с помощью метода неопределённых коэффициентов найдите многочлены U(x) и V(x) так, чтобы выполнялось равенство: f(х) × U(x) + g(x) × V(x) = d(x). Сделайте проверку. 1)f(х) = x3 , g(х) = (1 – x )2 ; 2)f(х) = 2 x4 + 3 x3 – 3 x2 – 5 x + 2 , g(х) = 2 x3 + x2 – х – 1 . В примерах 101 – 107докажите свойства наибольшегообщегоделителя многочленов. 101.Если f(x) 102.НОД ( f(x) ¹ 0 , g(x) ) = g(x) , где g(x) ¹ 0 . 103.НОД [ f(x) × h(х) , g(x) × h(х) ] = h(х) × НОД ( f(x) , g(x) ) . 104.Если f(x) = g(x) + j(x), то НОД ( f(x) , g(x) ) = НОД ( g(x) ,j(x) ) . 105.НОД ( f(x) , g(x) ) = НОД ( g(x) – f(x) , g(x) ) . 106.НОД ( f(x) , f(x) – g(x) ) = НОД ( g(x), f(x) + g(x) ) . 107.НОД ( f(x) , g(x) ) = НОД (f(x) – g(x) , f(x) + g(x)) . 108.Используя свойство НОД, указанное в примере 103,найдитенаибольшийобщийделитель d(x) многочленов f(x) и g(x) : 1)f(х) = (x – 1)3 (x 2 + 2 ) и g(х) = (x – 1)2 (x 2 + 2 ) ; 2)f(х) = (x3 – 4 х ) (x – 2 ) и g(х) = (x4 – 8 х ) (x + 2 ) . В примерах 109 – 124даны многочлены f(x) и g(x). С помощью алгоритма Евклиданайдите многочлены U(x) и V(x) так, чтобы выполнялось равенство : f(х) × U(x) + g(x) × V(x) = d(x) , где d(x) – наибольший общий делитель многочленов f(x) и g(x) . Сделайте проверку. 109.f(х) = x4 + 2 x3 – x2 – 4 x – 2 , g(х) = x4 + x3 – x2 – 2 х – 2 . 110.f(х) = x5 + 3 x4 + x3 + x2 + 3 x + 1 , g(х) = x4 + 2 x3 + х + 2 . 111.f(х) = x3 + 3 , g(х) = x2 – 2 . 112.f(х) = x4 – x3 – 4 x2 + 4 x + 1 , g(х) = x2 – х – 1 . 113.f(х) = 3x7+6 x6 –3 x5 + 4x4 +14x3 – 6x2 – 4x + 4, g(х) = 3x6–3 x4 +7x3 – 6 х +2. 114.f(х) = 3 x3 – 7 x2 + 5 x – 1 , g(х) = x2 – 3 х + 2 . 115.f(х) = x3 – 3 , g(х) = x2 + 1 . 116.f(х) = x3 + 2 , g(х) = x2 – 1 . 117.f(х) = 2 x3 – x2 + 3 x – 4 , g(х) = x2 + х – 2 . 118.f(х) = 2 x3 + 1 , g(х) = x2 – 1 . 119.f(х) = 3 x3 – 2 x2 + 3 x – 7 , g(х) = x2 – х – 2 . 120.f(х) = x4 – 2 , g(х) = x2 + х + 3 . 121.f(х) = 3x5 + 5 x4 – 16 x3 – 6 x2 – 5 x – 6 , g(х) = 3x4 – 4x3 – x2 – х – 2 . 122.f(х) = 2 x3 + 3 x2 – 2 x – 3 , g(х) = x2 + х – 6 . 123.f(х) = 3x5 – 7 x3 + 3 x2 – 7 , g(х) = x6– 7x4 + 8 x3– 7 х + 7. 124.f(х) = 3 x4 – 6 x3 + 5 x2 + 2 x – 2 , g(х) = x5– 2 x4 + x3 + 7 x2 – 12 х +10. В примерах 125 – 130, используя определение взаимно простых многочленов, установите, какие парыданныхмногочленов f(x) и g(x) являются взаимно простыми. 125.f(х) = x2 – x + 2 и g(х) = х + 3 . 126.f(х) = x2 – x – 6 и g(х) = x2 + 2 x . 127.f(х) = 4 x2 – x – 3 и g(х) = 2 x2 – x –1 . 128.f(х) = 5 x2 – x – 6 и g(х) = x2 + 2 x . 129.f(х) = x3 – x2 – x + 1 и g(х) = x2 – 3 x – 4 . 130.f(х) = 2 x3 + x2 – 4 x + 1 и g(х) = x2 – x – 3 . В примерах 131 – 134 докажите свойства взаимно простых многочленов. 131.Если[ f(x) × g(х) ] 132.Если НОД ( f(x),j(x) )=1 и НОД (g(x),j(x) )=1, тоНОД ( f(x) × g(х),j(x)) =1. 133.Если f(x) 134.Если НОД ( f(x) , g(x) ) = d(x), то НОД ( f(x) : d(x), g(x) : d(x) ) = 1 . 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
.
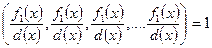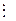h(x) и (f(x), h(х)) =1, то j(x) 
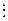h(x).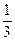
=q1(x)
x2 – 
x +1
x2 –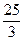 
x –10 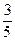= r1(x)
r1(x)
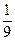r2(x)
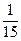r1(x) × q2(x), теперь выражаем r1(x) из предыдущего равенства: r1(x) = 3f(x) – g(x) × q1(x) и подставляем в полученное нами равенство, т.е.
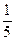f(x) × q2(x) – 
х– 1, V(x) = 
х.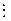
g(x) , где НОД (j(x), g (x) ) = 1, то f(x)