
|
|
НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ МНОГОЧЛЕНОВОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ Определение 5.1. Многочлен М(х) из кольца P[x] называется общим кратныммногочленов f(x) и g(x), тождественно не равных нулю из P[x], если М(х) делится без остатка на каждый из многочленов f(x) и g(x). Пример 5.1. Для трех многочленов f(x) = 2x − 6 Î R[x], g(x) = х + 2 Î R[x], d(x) = х − 1 многочлены М1(х) = (2x − 6)( х + 2)( х − 1)Î R[x], М2(х) = (2x − 6)( х + 2)( х − 1)(2х+10)Î R[x], М3(х) =(2x − 6)( х + 2)( х − 1) (х−10)Î R[x], М4(х) = (2x − 6)( х + 2)( х − 1) (2х+10) (х−10)Î R[x], М5(х) =(2x − 6)( х + 2)( х − 1)(х120 + х10 + х2)Î R[x], и, вообще, М6(х) =(2x − 6)( х + 2)( х − 1)× h(х), где h(х) – любой многочлен из R[x], будут их общими кратными. Определение 5.2. Многочлен т(х) из кольца P[x] называется наименьшим общим кратныммногочленов f(x) и g(x) из P[x], если т(х) является общим кратным многочленов f(x) и g(x) и любое другое общее кратное этих многочленов делится без остатка на т(х). Пример 5.2. Для трех многочленов из примера 4.3. f(x) = 2x − 6 Î R[x], g(x) = х + 2 Î R[x], d(x) = х − 1 наименьшим общим кратным будет многочлен т(х) = М1(х) = (2x − 6)( х + 2)( х − 1)Î R[x], т. к. на этот многочлен делятся все другие многочлены – общие кратные: М2(х) = (2x − 6)( х + 2)( х − 1)(2х+10)Î R[x], М3(х) =(2x − 6)( х + 2)( х − 1) (х−10)Î R[x], М4(х) = (2x − 6)( х + 2)( х − 1) (2х+10) (х−10)Î R[x], М5(х) =(2x − 6)( х + 2)( х − 1)(х120 + х10 + х2)Î R[x], и, вообще, М6(х) =(2x − 6)( х + 2)( х − 1)× h(х), где h(х) – любой многочлен из R[x]. Наименьшее общее кратное (НОК) обозначается символами: т (x) = [f(x), g(x)]. Теорема 5.1 [f 1(x), f2(x), f3(x),… fn(x)]=[[(x), f2(x), f3(x),… fn-1(x)] fn(x)]. Пример 5.3. Найдём наименьшее общее кратное многочленовf1(x) = x3 +x2 –x –1, f2(x) = x3 –x2 –x +1, f3(x) = x3 –x. По Теореме 5.1. [f1(x), f2(x), f3(x)]=[[f1(x), f2(x)], f3(x)]. Т.е. для того, чтобы найти НОК m(x ) трёх многочленов f1(x), f2(x), f3(x), необходимо найти НОК m 1(x ) двух многочленов f1(x), f2(x), а затем нужно найти НОK m2(x ) двух многочленов m1(x ) и f3(x). И m2(x ) = m(x) (Теорема 5.1.). Итак, [f1(x), f2(x)] = m1(x ) = (x2 –1)(x + 1)(x – 1), а [m1(x ), f3(x)] = m(x ) = x (x2 –1) (x + 1)(x – 1) = [f1(x), f2(x), f3(x)]. Теорема 5.2 Если d(x) и т(х) – соответственно наибольший общий делитель и наименьшее общее кратное многочленов f(x) и g(x), то d(x) × т(х) = f(x) × g(x).
Пример 5.4. Даны многочлены f(x) = х2 + 2х + 1; g(x) = х2 – 1. Их d(x) = х + 1; т(х) = (х2 + 2х + 1)( х – 1). Покажем справедливость Теоремы 5.2. d(x) × т(х) = (х + 1) × (х2 + 2х + 1)( х – 1) =(х2 + 2х + 1) × (х + 1)× ( х – 1) = (х2 + 2х + 1) × (х2 – 1) = f(x) × g(x).
УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ / Обозначения: т (x) = НОК ( f(x), g(x) ) или т (x) = [ f(x), g(x) ] / 135.Даны многочлены f(x) = х – 1 и g(x) = х + 1 . 1)Составьте 3 – 4 многочлена, являющихся кратными многочлена f(x) ; 2)Составьте 3 – 4 многочлена, являющихся кратными многочлена g(x) ; 3)Составьте 2 – 3 многочлена, являющихся общими кратными многочленов f(x) и g(x); 4)Составьте многочлен, являющийся наименьшим общим кратным многочленов f(x) и g(x) и убедитесь в том, он удовлетворяет всем требованиям, содержащимся в определении наименьшего общего кратного многочленов. 136.Составьте наименьшее общее кратное многочленов : f(х) = x2 – 4 , g(х) = (x – 2)2 , j(x) = x2 – 2 x . 137.Составьте наименьшее общее кратное и наибольший общий делитель многочленов f(х) = x2 – 9 и g(х) = (x+3)2. Проверьте справедливость равенства т(х)×d(x) = f(x)×g(x). В примерах 138 – 141используя равенство из примера 137,найдите наименьшее общее кратное многочленовf(х) и g(х) . 138.f(х) = 2 x3 – x + 14 и g(х) = x2 + x – 2 . 139.f(х) = 2 x3 + x + 3 и g(х) = x2 – x – 2 . 140.f(х) = x3 – 6 x2 + 11 x – 6 и g(х) = x2 + x – 6 . 141.f(х) = 3 x4 – 4 x3 + 7 x2 – 8 x + 2 и g(х) = 3 x4 – 4 x3 + 4 x2 – 4 x + 1. 142.Докажите свойства наименьшего общего кратного многочленов : 10.Если НОД ( f(x) , g(x) ) = 1, то НОК ( f(x) , g(x) ) = f(x) × g(x) . 20.Если НОД ( f(x) , g(x) ) = d(x) и НОК ( f(x) , g(x) ) = т(x), то т(x) 30.НОК [ f(x) × h(х) , g(x) × h(х) ] = h(х) × НОК ( f(x) , g(x) ) . 40.Если НОК ( f(x) , g(x) ) = т(x), то НОД [ т(x) : f (x), т(x) : g (x) ] = 1 . 143.Проверьте справедливость свойства 10из примера 142для многочленов f(х) = x3 – x2 и g(х) = x2 – 4 . 144.Используя свойства 20 и 10 из примера 142, найдите НОК ( f(x) , g(x) ), если : 1)f(х) = x2 (x + 2) , g(х) = x (x + 2)2 ; 2)f(х) = x (x – 1)2 (x – 3)3 , g(х) = x2 (x – 1) (x – 3)2 (x + 1) . НЕПРИВОДИМЫЕ И ПРИВОДИМЫЕ МНОГОЧЛЕНЫ НАД ПОЛЕМ. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА В ПРОИЗВЕДЕНИЕ МНОГОЧЛЕНОВ, НЕПРИВОДИМЫХ НАД ДАННЫМ ПОЛЕМ ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ Неприводимые и приводимые многочлены Над полем Пусть P[x] – кольцо многочленов от одной переменной с коэффициентами из поля Р P[x]= { anxn + an-1xn-1 + … + a1x + a0 | aiÎ P }. Определение 6.1. Многочлен f(x) п-й степени ( п > 0) из P[x] называется приводимым над полем Р, если он представим в виде произведения двух многочленов из того же кольца P[x], причём их степени ненулевые и меньшие п. В противном случае многочлен f(x) называется неприводимым над полем Р . Многочлен нулевой степени не является ни приводимым, ни неприводимым над заданным полем. Пример 6.1. Многочлен f(x) = х3– 1 – приводим над полем действительных чисел R, т.к. он представим в виде произведения двух многочленов из того же кольца R[x], причём их степени ненулевые и меньшие n: f(x) = х3– 1 = (x–1)(x2 + x +1) = p1(x)p2(x), deg f(x) = 3, deg p1(x) = 1, deg p2(x) = 2. Пример 6.2. Многочлен f(x) = х2+ 1 – неприводим над полем действительных чисел R, т.к. он не может быть представлен в виде произведения двух многочленов из того же кольца R[x] так, чтобы их степени были ненулевые и меньшие n. Однако над полем комплексных чисел С многочлен f(x) = х2+ 1 – приводим, т.к. он представим в виде произведения двух многочленов из того же кольца С[x], причём их степени ненулевые и меньшие n: f(x) = х2+ 1 = (x + i)( x – i) = p1(x)p2(x), deg f(x) = 2, deg p1(x) = 1, deg p2(x) = 1. Отметим,что здесь везде речь идёт о нетривиальных разложениях, т.к. любой многочлен имеет тривиальное разложение в произведение 1 и самого многочлена с точностью до ассоциированности: f(x) = 1 × f(x) = (5 ∙ При помощи понятия «тривиальное разложение многочлена в произведение» приводимый и неприводимый многочлены можно определить так: Определение 6.1.б. Многочлен f(x) п-й степени ( п > 0) из P[x] называется неприводимым над полем Р, если он допускает только тривиальное разложение в произведение, и приводимым над полем Р, если он допускает иные, кроме тривиального, разложения в произведение. Многочлен нулевой степени не является ни приводимым, ни неприводимым над заданным полем. *В теории делимости многочленов неприводимые многочлены в некотором смысле играют роль простых чисел в кольце целых чисел Z . Свойства неприводимых многочленов из кольца многочленов P[x]. Свойство 6.1.Многочлен 1й степени f (x) = ax+b неприводим над любым полем. o Это очевидно, т.к. многочлен 1й степени нельзя представить в виде произведения двух многочленов степеней ненулевых и меньших п (Определение 6.1.).· Свойство 6.2.Если произведение (f 1(x) × f2(x) × f3(x) × … × fs(x)) oДоказательство проведится методом математической индукции (ММИ) по s – количеству многочленов в произведении f 1(x) × f2(x) × f3(x) × … × fs(x). Свойство 6.3.Всякий многочлен p(x) степени n (n³2), имеющий корень в поле Р, приводим над этим полем. Свойство 6.4.4. Если р(х) и q(x) – неприводимые многочлены над Р и р(х) Свойство 6.5.Всякий многочлен степени п=2 или п=3 неприводим в поле Р тогда и только тогда, когда он не имеет корней в этом поле. o Доказательство от противного.· 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
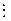 d(x) .
d(x) .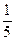 ) × f(x) = 5 ∙(
) × f(x) = 5 ∙(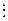 p(x), где p(x) – неприводимый над Р многочлен, то хотя бы один из сомножителей делится на p(x).
p(x), где p(x) – неприводимый над Р многочлен, то хотя бы один из сомножителей делится на p(x).