
|
|
Разложение многочлена в произведение многочленов, неприводимых над данным полемТеорема 6.1. Всякий многочлен f(x) из кольца P [x] степени n (n ¹0) может быть представлен в виде произведения неприводимых над полем P многочленов pi (x): f(x) = p1(x) × p2(x) × . . . ×ps (x), pi (x) Î P[x], 1 £ i £ s. (*) Это разложение является единственным с точностью до ассоциированности и до порядка следования множителей. o 1. Возможность представления доказывается методом математической индукции (ММИ) по п = deg f(x). I шаг ММИ. n = 1, т.е. многочлен степени 1 f(x)=a1x+a0. Такой многочлен неприводим над Р (Свойство 6.1.) II шаг ММИ. Предположим, что Теорема 6.1. (первая часть о возможности представления) верна для любого многочлена степени меньше п (n ¹ 0) . (Индуктивное предположение: всякий многочлен f(x) из кольца P [x] степени меньше п (n ¹ 0) может быть представлен в виде произведения неприводимых над полем P многочленов pi (x): f(x) = p1(x) × p2(x)× . . .× ps (x), pi (x) Î P[x], 1 £ i £ s). Докажем, что Теорема 6.1. верна для любого многочлена f(x) ÎP[x] степени п (n ¹ 0). Возможны два случая: а) f(x) – неприводим над Р, тогда это то, что и требовалось доказать (произведение неприводимых многочленов содержит один сомножитель f(x) = f(x), неприводимый над Р).× б) f(x) – приводим над Р => f(x)=f1(x) × f2(x), где deg f1(x)< n, deg f2(x)< n. Тогда для каждого из многочленов f1(x), f2(x) можно применить индуктивное предположение и найти для них представление в виде произведения неприводимых многочленов, а затем перемножить их. Тогда получим произведение неприводимых многочленов для многочлена f(x). 2. Единсвенность представления доказывается методом математической индукции (ММИ) по п = deg f(x). I шаг ММИ. n = 1, т.е. многочлен степени 1 f(x)=a1x+a0. Это представление единственное с точностью до ассоциированности, т.е. f(x) = ax+b = = c × (a × c-1x+b × c-1), где с - любой обратимый элемент поля Р. II шаг ММИ. Предположим, что Теорема 6.1. (вторая часть о единственности представления) верна для любого многочлена степени меньше п (n ¹ 0) . (Индуктивное предположение: всякий многочлен f(x) из кольца P [x] степени меньше п (n ¹ 0) может быть представлен в виде произведения неприводимых над полем P многочленов pi (x): f(x) = p1(x) × p2(x)× . . .× ps (x), pi (x) Î P[x], 1 £ i £ s), причём единственным образом с точностью до ассоциированности и до порядка следования множителей). Докажем, что Теорема 6.1. (вторая часть о единственности представления) верна для любого многочлена f(x) ÎP[x] степени п (n ¹ 0),т.е., что представление в виде произведения неприводимых над этим полем многочленов единственно для любых многочленов степени п (n ¹ 0) (с точностью до ассоциированности и до порядка следования множителей). Возможны два случая: а) f(x) –неприводим над Р, тогда это то, что и требовалось доказать (произведение неприводимых многочленов содержит один сомножитель, неприводимый над Р, и это произведение единственное). б) f(x) – приводим над Р, т.е. f(x) раскладывается в произведение неприводимых над Р сомножителей: (*). Надо доказать, что это призведение единственно с точностью до ассоциированности и до порядка следования множителей Докажем от противного: предположим, что такое представление в виде произведения неприводимых над полем Р многочленов не единственно; пусть их хотя бы два: f(x) = p1(x) × p2(x) × …ps(x), f(x) = q1(x) × q2(x) × … × qt(x), где pi(х), qi(х) – неприводимы над Р, и pi(х) ¹ qi(х). Левые части этих равенств одинаковы, следовательно, правые части этих равенств тоже одинаковы: p1(x) × p2(x) × …ps(x) = q1(x) × q2(x) × … × qt(x)(**). Левая часть последнего равенства делится на p1(x) => правая часть тоже делится на р1(х). Но по свойству неприводимых многочленов (Свойство 6.4.)какой-то из многочленов qi(x) = c1 × p1(x) = c1p1(x). Подставим в (**)вместо многочлена qi многочлен c1p1(x): p1(x) × p2(x) × … × ps(x) = q1(x) × q2(x) × … qi-1(x) × c1p1(x) × qi+1(x) × … × qt(x). Обе части получившегося равенства сокращаем на p1(x): p2(x) × … × ps(x) = q1(x) × q2(x) × … qi-1(x) × c1 × qi+1(x) × … × qt(x) (***). После сокращения обеих частей равенства на неприводимый многочлен p1(x) (deg p1(x) ≥ 1) степени многочленов слева и справа в равенстве (***)стали меньше п, и мы можем применить индуктивное предположение, которое гласит, что многочлены степени меньшей п раскладываются в произведения неприводимых многочленов единственным образом (с точностью до ассоциированности и до порядка следования множителей: т.е. s=t и каждое pk(x)=qj(x), где 1≤ к≤ s, 1≤ j≤ t = s. Домножив обе части последнего равенства (***) на р1(х), получим опять однозначное разложение, теперь для многочлена f(x). · Определение 6.2. Некоторыймногочлен p(х)Î P[x] называется k – кратным множителем многочлена f(x) Î P[x], если f(x) делится на pk(х), но не делится на pk+1(х), где k – целое неотрицательное число. Пример 6.3. Многочлен f(x) = 6х6 –12 х3+ 6 имеет следующее каноническое разложение f(x) = 6х6 –12 х3+ 6 = 6(х2 + х + 1)2(х2 – 1)2. ТИПОВЫЕ ЗАДАЧИ Задача 1. Установить, является ли многочлен f(x) неприводимым над полем Q, над полем R, над полем C, если: 1)f(x) = x3 + x2 – 2 x – 2; 2)f(x) = x4 + 9; 3)f(x) = x2 + 5. . Решение. 1)f(x) = x3 + x2 – 2 x – 2 = (x3 + x2) – (2 x + 2) = x2 (x + 1) – 2 (x + 1) = = (x + 1) (x2 – 2). Многочлен f(x) разложен на множители, причём каждый множитель имеет степень, меньшую, чем степеньмногочлена f(x). И так как они являются многочленами с рациональными коэффициентами, то по определению (Определение 6.1.) многочлен f(x) приводим над Q, а значит и над полями R и C . При этом над полями R и C многочлен f(x) может быть представлен в виде: f(x) = (x + 1) (x – 2)f(x) = x4 + 9 = (x4 + 6 x2 + 9) – 6 x2 = (x2 + 3)2 – 6 x2 = (x2 + 3)2 – ( Многочлен f(x) разложен в произведение двух многочленов, причём каждый множитель имеет степень меньшую, чем степеньмногочлена f(x). И так как эти множители являются многочленами с действительными (в частности, иррациональными) коэффициентами, то, по определению 1, многочлен f(x) является приводимым над полями R и C и неприводимым над полем Q. При этом над полем C многочлен f(x) имеет следующее разложение: f(x)= 3)f(x) = x2 + 5 = x2 – ( Многочлен f(x) разложен в произведение двух многочленов, причём каждый множитель имеет степень меньшую, чем степеньмногочлена f(x). И так как коэффициенты этих множителей – комплексные числа, то многочлен f(x) является приводимым над полем C и неприводимым над полями Q и R. УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ 145.Даны многочлены из кольца многочленов С [x] над полем С : 1)x + 1 , 2)3x – 7 , 3)x2 – 4,4) x2 – 3 , 5) x2 + 4 , 6) x3 – 1, 7) x3 + 8) x4 + 4 , 9) x – а)Выпишите те многочлены, которые являются неприводимыми над полем Q ; б)Выпишите те многочлены, которые являются неприводимыми над полем R ; в)Выпишите те многочлены, которые являются неприводимыми над полем C . В примерах 146 – 168данные многочлены указанными ниже способами разложите на неприводимые множители над полем R: а)используя способ группировки или подобрав один из корней многочлена и с помощью схемы Горнера понизив его степень : 146.x3 – 3 x2 + 4 x – 2. 147.x3 – 6 x2 + 11 x – 6. 148.x3 – 4 x2 + x + 6. 149. х4 – 5 x3 + 3 x2 + 5 x – 4. 150.x3 + x2 – 10 x + 8. 151.x3 – 9 x2 + 26 x – 24.152.x3 – 12 x2 + 47 x – 60. 153.х4 – x3 – x + 1. 154. х4 + 8 x3 + 23 x2 + 28 x + 12. б)используя способ “разбиения” одного из коэффициентов многочлена : 155.x3 + x + 2. 156.x3 + x + 10. 157.х4 + 3 x2 + 4. 158.x4 – 3 x2 + 1. 159.3 х3 – 2 x + 1. 160.х4 – 10 x2 + 1. в)используя способ “добавить и вычесть” и формулы сокращённого умножения: 161.x4 + 4. 162.х4 + 1. 163.х4 + x2 + 1. 164.x4 + 16. 165.x6 – 1. 166.х4 – 3 x2 + 9. 167.х4 + 2 В примерах 169 – 172данные многочлены разложите, если это возможно, на неприводимые множители а)над полем Q ; б) над полем R ; в)над полем С . 169.f(х) = x4 – 1. 170.j(x) = x4 – 3 x2 – 10. 171.g(х) = x6 + 27.172.h(х) = x4 + 3 x2 + 9. 173.Разложите на неприводимые множители над полем R многочлен f(х) = x4 – а x2 + 1 , где – 2 < a < 2 . 174.Докажите следующие свойства неприводимых над полем Р многочленов: 10.Если f(x) – произвольный многочлен из кольца P [x], р(х) – неприводимый мно– гочлен над полем Р , то либо f (x) 20.Если р(x) и q(x) – неприводимые многочлены над полем Р и р(x) 30.Если р(x) и q(x) – неприводимые многочлены над полем Р и р(x) и q(x) – неассоциированные многочлены (то есть q(x) ¹ с × р(x), где сÎР ), то НОД( р(x), q(x) )= 1. 40.Если [ f(x) × g(x) ] 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
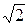 ) (x +
) (x +  x)2 = = (x2 –
x)2 = = (x2 – 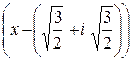 ×
× 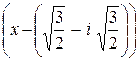 ×
×  ×
×  .
. i )2 = (x +
i )2 = (x +  ,
, x2 + 1. 168.х2 +
x2 + 1. 168.х2 + 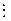 р(x) , либо НОД ( f(x) , р(x) ) = 1.
р(x) , либо НОД ( f(x) , р(x) ) = 1.