Плоское движение твёрдого тела
Плоским, или плоскопараллельным, движением твёрдого тела называется такое движение, при котором все точки тела движутся в плоскостях, параллельных некоторой неподвижной плоскости (иногда эту плоскость называют плоскостью параллелизма или основной плоскостью).
Плоское движение, например, совершает цилиндр  , который катится по горизонтальной неподвижной плоскости (рис. 15). В кривошипно-ползунном механизме плоское движение совершает шатун AB (рис. 16). , который катится по горизонтальной неподвижной плоскости (рис. 15). В кривошипно-ползунном механизме плоское движение совершает шатун AB (рис. 16).
  Все точки цилиндра A шатуна AB движутся в плоскостях, параллельных вертикальной плоскости. Все точки цилиндра A шатуна AB движутся в плоскостях, параллельных вертикальной плоскости.
    При плоском движении тела прямые, проведенные в теле перпендикулярно плоскости параллелизма, движутся поступательно, поэтому для изучения плоского движения тела достаточно изучить движение плоской фигуры, которая получается при сечении тела плоскостью, параллельной плоскости параллелизма. Так, для изучения плоского движения цилиндра При плоском движении тела прямые, проведенные в теле перпендикулярно плоскости параллелизма, движутся поступательно, поэтому для изучения плоского движения тела достаточно изучить движение плоской фигуры, которая получается при сечении тела плоскостью, параллельной плоскости параллелизма. Так, для изучения плоского движения цилиндра  (рис. 15) достаточно изучить качение по неподвижной горизонтальной прямой катка, радиус которого равен радиусу основания цилиндра (рис. 17). Для задания движения плоской фигуры в плоскости (рис. 15) достаточно изучить качение по неподвижной горизонтальной прямой катка, радиус которого равен радиусу основания цилиндра (рис. 17). Для задания движения плоской фигуры в плоскости 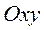 необходимо задать законы изменения координат необходимо задать законы изменения координат  и и  некоторой её точки некоторой её точки  (рис. 18), с которой связывается подвижная система отсчёта (рис. 18), с которой связывается подвижная система отсчёта  и угол и угол 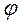 , характеризующий поворот подвижной системы отсчёта , характеризующий поворот подвижной системы отсчёта  относительно неподвижной относительно неподвижной 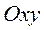 . Выражения . Выражения
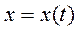 , , 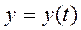 , ,  (2.20) (2.20)
 называются кинематическими уравнениями плоского движения твёрдого тела. Из теоремы о разложении плоского движения тела на поступательное вместе с полюсом и вращательное относительно полюса следует: движение фигуры называются кинематическими уравнениями плоского движения твёрдого тела. Из теоремы о разложении плоского движения тела на поступательное вместе с полюсом и вращательное относительно полюса следует: движение фигуры  в плоскости в плоскости  можно любым бесконечным числом способов представить как совокупность двух движений – поступательного вместе с полюсом можно любым бесконечным числом способов представить как совокупность двух движений – поступательного вместе с полюсом  и вращательного относительно полюса и вращательного относительно полюса  ; при этом кинематические параметры поступательного движения фигуры ; при этом кинематические параметры поступательного движения фигуры  (скорость и ускорение полюса) от выбора полюса зависят; параметры же вращательного движения фигуры (угловая скорость (скорость и ускорение полюса) от выбора полюса зависят; параметры же вращательного движения фигуры (угловая скорость  и угловое ускорение и угловое ускорение  ) от выбора полюса независят. ) от выбора полюса независят.
 Между скоростями точек плоской фигуры существует зависимость, которая определяется теоремой: скорость любой точки Между скоростями точек плоской фигуры существует зависимость, которая определяется теоремой: скорость любой точки  фигуры фигуры  (рис. 19) равна геометрической сумме скорости (рис. 19) равна геометрической сумме скорости 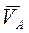 точки точки  , принятой за полюс, и скорости , принятой за полюс, и скорости  вращения точки вращения точки  вместе с фигурой вместе с фигурой  вокруг полюса вокруг полюса  : :
 . (2.21) . (2.21)
По модулю  , а вектор , а вектор  направлен направлен  в сторону круговой стрелки в сторону круговой стрелки  . Согласно выражению (2.21), скорость . Согласно выражению (2.21), скорость 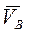 направлена по диагонали параллелограмма, построенного на векторах направлена по диагонали параллелограмма, построенного на векторах 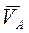 и и  . Спроектировав векторное равенство (2.21) на направление прямой . Спроектировав векторное равенство (2.21) на направление прямой  , получаем теорему о проекциях скоростей: проекции скоростей двух точек плоской фигуры на прямую, соединяющую эти точки, равны между собой. , получаем теорему о проекциях скоростей: проекции скоростей двух точек плоской фигуры на прямую, соединяющую эти точки, равны между собой.
Так, для скоростей, изображенных на рис. 19, согласно теореме о проекциях скоростей, имеем:
 . (2.22) . (2.22)
Теорема о проекциях скоростей позволяет наиболее просто решить задачу определения скорости любой точки плоской фигуры, если известны направление скорости этой точки и скорость любой другой точки фигуры.
 Картина распределения скоростей точек плоской фигуры наглядно определяется, если найден её мгновенный центр скоростей (МЦС). Согласно теореме о МЦС, при непоступательном движении плоской фигуры (рис. 20) в каждый момент времени существует такая единственная точка P, скорость которой в данный момент времени равна нулю и которая называется мгновенным центром скоростей. Если для плоской фигуры S известны (рис. 20) скорость некоторой точки A и угловая скорость Картина распределения скоростей точек плоской фигуры наглядно определяется, если найден её мгновенный центр скоростей (МЦС). Согласно теореме о МЦС, при непоступательном движении плоской фигуры (рис. 20) в каждый момент времени существует такая единственная точка P, скорость которой в данный момент времени равна нулю и которая называется мгновенным центром скоростей. Если для плоской фигуры S известны (рис. 20) скорость некоторой точки A и угловая скорость  , то для определения МЦС необходимо повернуть вектор , то для определения МЦС необходимо повернуть вектор 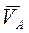 вокруг точки A на угол 90° в сторону круговой стрелки вокруг точки A на угол 90° в сторону круговой стрелки  и на полученной при этом прямой AL отложить отрезок AP, равный и на полученной при этом прямой AL отложить отрезок AP, равный
 . .
Полученная таким образом точка P – МЦС фигуры S.
Скорость точки P равна нулю только в данный момент времени. В следующий момент времени картина распределения скоростей плоской фигуры меняется, и МЦС меняет своё положение, поэтомуточка P называется мгновенным центром скоростей.
МЦС может находиться и за пределами плоской фигуры.
Отображение МЦС на неподвижной плоскости дает мгновенный центр вращения (МЦВ).
Относительно МЦС скорости точек плоской фигуры распределяются так, как будто фигура вращается в данный момент времени вокруг МЦС. Таким образом, если для плоской фигуры (рис. 21) известны МЦС (точка P) и угловая скорость  , то скорости любых точек A и B фигуры равны , то скорости любых точек A и B фигуры равны
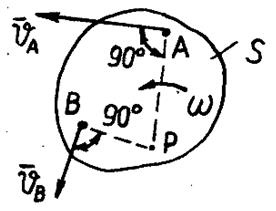  . (2.23) . (2.23)
Векторы 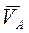 и и 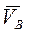 направлены перпендикулярно соответственно отрезкам направлены перпендикулярно соответственно отрезкам  и и  в сторону круговой стрелки в сторону круговой стрелки  . .
 Из рисунка видно, что для определения МЦС в общем случае необходимо знать направление скоростей двух любых точек Из рисунка видно, что для определения МЦС в общем случае необходимо знать направление скоростей двух любых точек  и и  плоской фигуры. МЦС находится на пересечении перпендикуляров, восстановленных к векторам плоской фигуры. МЦС находится на пересечении перпендикуляров, восстановленных к векторам 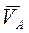 и и 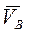 в точках в точках  и и  . .
Разделив первое выражение (2.23) на второе, получаем:
  . .
Следовательно, скорости точек плоской фигуры пропорциональны их расстояниям до МЦС.
Рассмотрим некоторые частные случаи определения МЦС.
1. Если тело  (рис. 22)катится без скольжения по неподвижной поверхности (рис. 22)катится без скольжения по неподвижной поверхности  , то для тела , то для тела  МЦС (точка P) находится в точке контакта тела с поверхностью. МЦС (точка P) находится в точке контакта тела с поверхностью.
 2. Если для двух точек 2. Если для двух точек  и и  (рис. 23а,б) плоской фигуры (рис. 23а,б) плоской фигуры  и и  , то МЦС находится на пересечении прямой , то МЦС находится на пересечении прямой  и линии, соединяющей концы векторов и линии, соединяющей концы векторов 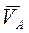 и и 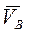 . .

3. Если для двух точек  и и  фигуры (рис. 24) фигуры (рис. 24)  , то МЦС находится в , то МЦС находится в  , тогда угловая скорость фигуры , тогда угловая скорость фигуры
 . .
 В этом случае скорости всех точек фигуры одинаковы по модулю и направлению и фигура либо движется поступательно, либо происходит мгновенное распределение скоростей фигуры, как при поступательном движении. В этом случае скорости всех точек фигуры одинаковы по модулю и направлению и фигура либо движется поступательно, либо происходит мгновенное распределение скоростей фигуры, как при поступательном движении.

Ускорения точек плоской фигуры определяются согласно теореме: ускорение  любой точки любой точки  плоской фигуры (рис. 25) равно геометрической сумме ускорения плоской фигуры (рис. 25) равно геометрической сумме ускорения  точки А, принятой за полюс, вращательного точки А, принятой за полюс, вращательного  и центростремительного и центростремительного  ускорений при вращении точки ускорений при вращении точки  вместе с фигурой вокруг полюса вместе с фигурой вокруг полюса  : :
 . (2.24) . (2.24)
Для определения ускорения  по равенству (2.24) находим и направляем ускорения по равенству (2.24) находим и направляем ускорения  и и  , ,
 , вектор , вектор  направлен направлен  в сторону в сторону  ; ;
 , вектор , вектор  направлен по направлен по  от от  к к  . .
Суммируя геометрически  и и  , находим: , находим:
 . .
 – ускорение при вращении точки – ускорение при вращении точки  вместе с фигурой вокруг полюса вместе с фигурой вокруг полюса  . .
Тогда согласно (2.24) ускорение  направлено по диагонали параллелограмма, построенного на векторах направлено по диагонали параллелограмма, построенного на векторах  и и  . .
Вектор ускорения  образует с отрезком образует с отрезком  угол угол  (рис. 25), причём (рис. 25), причём
 и и  . (2.25) . (2.25)
 Аналогично МЦС для плоской фигуры при непоступательном её движении существует мгновенный центр ускорения (МЦУ). Аналогично МЦС для плоской фигуры при непоступательном её движении существует мгновенный центр ускорения (МЦУ).  – это точка, ускорение которой в данный момент времени равно нулю. Если для плоской фигуры известны ускорение – это точка, ускорение которой в данный момент времени равно нулю. Если для плоской фигуры известны ускорение  некоторой точки некоторой точки  (рис. 26), угловая скорость (рис. 26), угловая скорость  и угловое ускорение и угловое ускорение  , то для определения МЦУ необходимо: , то для определения МЦУ необходимо:
 - определить угол - определить угол  по выражению (2.26); по выражению (2.26);
- повернуть вектор  вокруг точки вокруг точки  на угол на угол  в сторону вращения в сторону вращения  ; ;
- на прямой  отложить отрезок отложить отрезок  . .
Получим МЦУ – точку  . .
Сказанное о МЦС характерно и для МЦУ:
а) МЦУ  может находиться за пределами плоской фигуры; может находиться за пределами плоской фигуры;
б) ускорения точек плоской фигуры распределяются так, будто фигура вращается в данный момент времени вокруг МЦУ;
в) ускорения точек плоской фигуры пропорциональны их расстояниям до МЦУ.
Если для плоской фигуры (рис. 26) известны МЦУ – точка  , угловая скорость , угловая скорость  и угловое ускорение и угловое ускорение  , то ускорение любой точки , то ускорение любой точки  фигуры равно фигуры равно
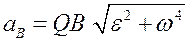 , ,
и вектор  образует с отрезком образует с отрезком 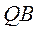 угол угол  , который определяется выражением (2.25). Угол , который определяется выражением (2.25). Угол  откладывается от отрезка откладывается от отрезка 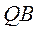 так, чтобы вектор так, чтобы вектор  был направлен в сторону был направлен в сторону  . .
Рассмотрим наиболее характерные примеры решения задач по кинематике плоского движения твёрдого тела.
 Пример 1. Отрезок Пример 1. Отрезок  (рис. 27) движется в плоскости чертежа. Известна скорость (рис. 27) движется в плоскости чертежа. Известна скорость 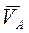 точки точки  отрезка и направление скорости отрезка и направление скорости 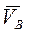 конца конца  . Определить скорости точек . Определить скорости точек  и и 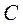 отрезка, если отрезка, если 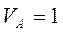 м/с, м/с,  , ,  м, м,  и и 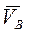 направлена по направлена по  . .
Можно указать несколько способов решения этой задачи. Некоторые из них базируются на основном векторном равенстве (2.21)
 . .
Однако в данной задаче, как и в большинстве других задач, наиболее просто картина распределения скоростей точек отрезка  может быть получена с помощью МЦС. МЦС отрезка может быть получена с помощью МЦС. МЦС отрезка  можно получить исходя из общего случая: восстанавливаем перпендикуляры к векторам можно получить исходя из общего случая: восстанавливаем перпендикуляры к векторам 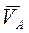 в точке в точке  и и 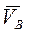 в точке в точке  . Точка . Точка  находится на пересечении указанных перпендикуляров. находится на пересечении указанных перпендикуляров.
Тогда угловая скорость отрезка
 рад/с, рад/с,
и  направлена в ту сторону, куда направлена в ту сторону, куда 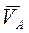 вращает вращает  относительно точки относительно точки  . .
Зная  , находим скорости точек В и С: , находим скорости точек В и С:
 м/с; м/с;
 Скорость Скорость  направлена направлена  в сторону в сторону  . .
Аналогично точке С можно найти модуль и направление скорости любой другой точки отрезка.
Если в задаче известна скорость одной точки и направление скорости другой точки, то скорость этой точки наиболее просто определяется с помощью теоремы о проекциях скоростей двух точек плоской фигуры на прямую, соединяющую эти точки. Согласно этой теореме
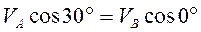 , ,
откуда  м/с. м/с.
Пример 2.В положении механизма, указанном на рис. 28, определить скорость точки  , если , если  м, м,  м, м, 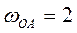 рад/с, рад/с,  рад/с. Направление угловых скоростей рад/с. Направление угловых скоростей 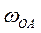 и и  указано на рисунке. указано на рисунке.
В механизме, рассматриваемом в данном примере, звенья  и и  совершают плоское движение. Поскольку направление скорости точки совершают плоское движение. Поскольку направление скорости точки  механизма неизвестно, указать положение МЦС звеньев сразу нельзя, поэтому данную задачу можно решить с использованием векторных равенств (2.21). механизма неизвестно, указать положение МЦС звеньев сразу нельзя, поэтому данную задачу можно решить с использованием векторных равенств (2.21).
Находим скорости точек  и и 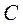
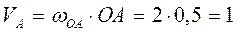 м/с; м/с; 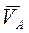 направлен направлен  в сторону в сторону 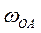 ; ;
 м/с; м/с;  направлен направлен 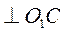 в сторону в сторону  . .
Согласно выражению (2.21), скорость точки 
 и и  . (2.26) . (2.26)
Из равенства левых частей записанных векторных равенств следует равенство и правых, следовательно,
 . (2.27) . (2.27)
В равенстве (2.27) неизвестны модули скоростей  и и  . Задаём направление указанных скоростей. Модули скоростей . Задаём направление указанных скоростей. Модули скоростей  и и  находим путём проектирования выражения (2.27) на две оси. Указанные оси можно выбрать произвольно, но для рационального решения задачи оси выбираем так, чтобы на каждую из них проектировалась одна из неизвестных скоростей равенства (2.27). находим путём проектирования выражения (2.27) на две оси. Указанные оси можно выбрать произвольно, но для рационального решения задачи оси выбираем так, чтобы на каждую из них проектировалась одна из неизвестных скоростей равенства (2.27).
Проектируем (2.27) на ось Bx
 , откуда , откуда 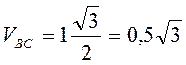 м/с. м/с.
Так как 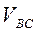 получилась со знаком «+», направление вектора получилась со знаком «+», направление вектора  на рис. 28указано верно. Проектируя (2.27) на вторую ось By, можно найти на рис. 28указано верно. Проектируя (2.27) на вторую ось By, можно найти 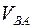 . Учитывая, что . Учитывая, что  , находим: , находим:
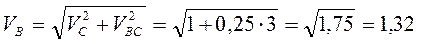 м/с. м/с.
Рассмотрим примеры решения задач на определение ускорений точек тела при плоском движении.
Для определения ускорения любой точки тела, совершающего плоское движение, в общем случае необходимо знать ускорение одной его точки 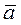 ,угловую скорость ,угловую скорость  и угловое ускорение и угловое ускорение  . По способу определения . По способу определения  все основные задачи можно условно разделить на две группы. К первой группе отнесём задачи, в которых плоское движение совершают тела типа катков, катящихся без скольжения по неподвижным телам. Все другие задачи отнесём ко второй группе. После определения все основные задачи можно условно разделить на две группы. К первой группе отнесём задачи, в которых плоское движение совершают тела типа катков, катящихся без скольжения по неподвижным телам. Все другие задачи отнесём ко второй группе. После определения 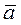 , ,  и и  ускорение любой точки тела определяется, как правило, одинаково с использованием векторного равенства (2.24). ускорение любой точки тела определяется, как правило, одинаково с использованием векторного равенства (2.24).
Рассмотрим решение характерных примеров задач первой (пример 3) и второй (пример 4) групп.
 Пример 3. В планетарном механизме (рис. 29) колесо 2 катится без скольжения по неподвижному колесу и приводится в движение кривошипом Пример 3. В планетарном механизме (рис. 29) колесо 2 катится без скольжения по неподвижному колесу и приводится в движение кривошипом  . Определить скорости и ускорения точек . Определить скорости и ускорения точек  и и 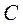 колеса 2 механизма, если колеса 2 механизма, если
 м, м,
 рад/с, рад/с,
 рад/с²и кривошип рад/с²и кривошип  вращается в данный момент времени замедленно. вращается в данный момент времени замедленно.
Для решения задачи зададим направление 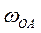 и и 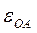 . Находим ускорение точки . Находим ускорение точки  колеса 2, его угловую скорость колеса 2, его угловую скорость  и его угловое ускорение и его угловое ускорение  . .
Ускорение точки  равно равно
 , ,
где  м/с²; м/с²; 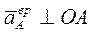 в сторону в сторону 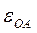 , ,
 м/с²; м/с²;  направлен по направлен по  от от  к к 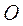 . .
Угловую скорость  удобно определять с помощью МЦС. Согласно первому частному случаю определения МЦС, для колеса 2 это точка удобно определять с помощью МЦС. Согласно первому частному случаю определения МЦС, для колеса 2 это точка  – точка контакта колес 1 и 2. Скорость точки – точка контакта колес 1 и 2. Скорость точки  колеса колеса
 м/с; м/с;  в сторону в сторону 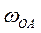 . .
Тогда угловая скорость колеса 2
 рад/с, рад/с,
и  направлена в ту сторону, в которую скорость направлена в ту сторону, в которую скорость 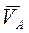 вращает колесо 2 относительно МЦС – точки P. вращает колесо 2 относительно МЦС – точки P.
Находим скорости точек  и и 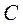 колеса 2 колеса 2
 м/с; м/с;  в сторону ω, в сторону ω,
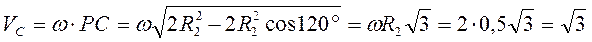 м/с; м/с;  в сторону в сторону  . .
В задачах первой группы угловое ускорение  определяется с учётом того, что для колеса 2 определяется с учётом того, что для колеса 2  . .
 рад/с². рад/с².
Угловое ускорение  направлено в ту сторону, в которую вектор направлено в ту сторону, в которую вектор 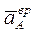 вращает колесо относительно МЦС – точки вращает колесо относительно МЦС – точки  . .
Принимая за полюс точку  , записываем векторное равенство для ускорения точки , записываем векторное равенство для ускорения точки  : :
 , ,
 м/с²; м/с²; 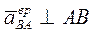 в сторону в сторону  , ,
 м/с²; м/с²;  направлен по AB от B к A. направлен по AB от B к A.
Для определения модуля ускорения  находим две его проекции на оси находим две его проекции на оси  и и 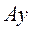 : :
 м/с²; м/с²;
 м/с². м/с².
Тогда  м/с². м/с².
Аналогично определяем ускорение точки 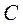 колеса 2 колеса 2
 . .
 м/с²; м/с²;  в сторону в сторону  , ,
 м/с²; м/с²;  направлен по СА от С к А. направлен по СА от С к А.
Находим проекции ускорения  на оси на оси  и и 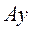
 м/с². м/с².
 м/с². м/с².
Ускорение точки С равно
 м/с². м/с².
 Пример 4. Кривошип Пример 4. Кривошип  кривошипно-ползунного механизма (рис. 30) вращается ускоренно, имея в данный момент времени угловую скорость кривошипно-ползунного механизма (рис. 30) вращается ускоренно, имея в данный момент времени угловую скорость 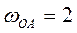 рад/си угловое ускорение рад/си угловое ускорение 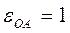 рад/с². Определить в заданном положении механизма скорость и ускорение точек рад/с². Определить в заданном положении механизма скорость и ускорение точек  и и 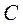 , если , если  м, м,  и и  . .
 Звено Звено  механизма совершает плоское движение. Для определения ускорения любой точки шатуна механизма совершает плоское движение. Для определения ускорения любой точки шатуна  необходимо, как и в примере 3, определить вначале ускорение одной его точки необходимо, как и в примере 3, определить вначале ускорение одной его точки 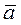 , угловую скорость , угловую скорость  и угловое ускорение и угловое ускорение  . .
Из условия задачи находим ускорение точки 
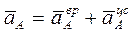 , ,
 м/с²; м/с²; 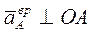 в сторону в сторону 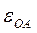 , ,
 м/с²; м/с²;  направлен по OA от A к O. направлен по OA от A к O.
Угловую скорость  шатуна шатуна  находим с помощью МЦС. Для этого определим скорость точки находим с помощью МЦС. Для этого определим скорость точки 
 м/с; м/с;  в сторону в сторону 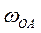 . .
МЦС точка P звена  находится на пересечении перпендикуляров к векторам скоростей находится на пересечении перпендикуляров к векторам скоростей 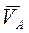 в точке в точке  и и 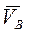 в точке в точке  . .
Угловая скорость шатуна
 рад/с, рад/с,
 направлена в ту сторону, в которую скорость направлена в ту сторону, в которую скорость 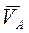 вращает звено вращает звено  относительно МЦС точки относительно МЦС точки  . .
Зная  и МЦС, находим скорости точек и МЦС, находим скорости точек  и и 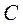 : :
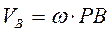 ; ;  м; м;
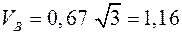 м/с; м/с;
 ; ;
 м; м;
 м/с. м/с.
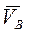 и и  направлены перпендикулярно соответственно направлены перпендикулярно соответственно  и и  в сторону в сторону  . .
В задачах второй группы для определения углового ускорения  записываем векторное равенство для ускорения точки записываем векторное равенство для ускорения точки  шатуна шатуна 
 . (2.28) . (2.28)
Из равенства (2.28) находим ускорение  , зная которое определяем , зная которое определяем  звена звена  . .
В векторном равенстве (2.28) ускорения, известные по модулю и направлению, подчеркнуты двумя чертами; известные только по направлению – одной чертой.
Находим ускорение 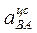
 м/с²; м/с²;  направлено по направлено по 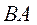 от от  к к  . .
Задаём направление  и и  . Модули ускорений . Модули ускорений  и и  находим путём проектирования равенства на две любые оси. Оси следует выбирать так, чтобы на каждую проектировалось только одно неизвестное ускорение равенства (2.28). находим путём проектирования равенства на две любые оси. Оси следует выбирать так, чтобы на каждую проектировалось только одно неизвестное ускорение равенства (2.28).
Проектируем (2.28) на ось  , направленную по , направленную по  : :
 ; ;
 м/с². м/с².
Поскольку  получилось со знаком «+», направление ускорения получилось со знаком «+», направление ускорения  указано верно. указано верно.
Проектируем (2.28) на ось 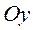
 , ,
 м/с². м/с².
Значит, направление ускорения  указано также верно. Зная указано также верно. Зная  , находим угловое ускорение звена , находим угловое ускорение звена  : :
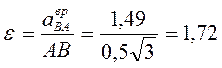 рад/с², рад/с²,
угловое ускорение  шатуна шатуна  направлено в ту сторону, в которую ускорение направлено в ту сторону, в которую ускорение  вращает звено относительно полюса вращает звено относительно полюса  . .
Поскольку для звена  известны ускорение точки известны ускорение точки   , ,  и и  , можно найти ускорение точки , можно найти ускорение точки 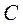 . .
Принимая за полюс точку  , записываем векторное равенство для ускорения точки , записываем векторное равенство для ускорения точки 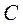 : :
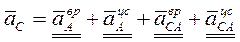 . (2.29) . (2.29)
В равенстве (2.29)
 м/с²; м/с²;  в сторону в сторону  , ,
 м/с²; м/с²;  направлен по направлен по 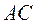 от от 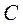 к к  . .
Находим проекции ускорения  на две перпендикулярные оси на две перпендикулярные оси  и и 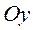
  м/с²; м/с²;
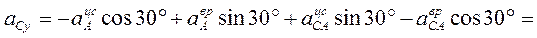  м/с². м/с².
Тогда
 м/с². м/с².
В задачах второй группы следует особо выделить подгруппу задач, в которых для тела, совершающего плоское движение, известны ускорения двух его точек и требуется определить ускорение любой другой точки тела.
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

 называются кинематическими уравнениями плоского движения твёрдого тела. Из теоремы о разложении плоского движения тела на поступательное вместе с полюсом и вращательное относительно полюса следует: движение фигуры
называются кинематическими уравнениями плоского движения твёрдого тела. Из теоремы о разложении плоского движения тела на поступательное вместе с полюсом и вращательное относительно полюса следует: движение фигуры  в плоскости
в плоскости 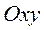 можно любым бесконечным числом способов представить как совокупность двух движений – поступательного вместе с полюсом
можно любым бесконечным числом способов представить как совокупность двух движений – поступательного вместе с полюсом  и вращательного относительно полюса
и вращательного относительно полюса  ; при этом кинематические параметры поступательного движения фигуры
; при этом кинематические параметры поступательного движения фигуры  (скорость и ускорение полюса) от выбора полюса зависят; параметры же вращательного движения фигуры (угловая скорость
(скорость и ускорение полюса) от выбора полюса зависят; параметры же вращательного движения фигуры (угловая скорость  и угловое ускорение
и угловое ускорение  ) от выбора полюса независят.
) от выбора полюса независят.
 . (2.21)
. (2.21)
 Картина распределения скоростей точек плоской фигуры наглядно определяется, если найден её мгновенный центр скоростей (МЦС). Согласно теореме о МЦС, при непоступательном движении плоской фигуры (рис. 20) в каждый момент времени существует такая единственная точка P, скорость которой в данный момент времени равна нулю и которая называется мгновенным центром скоростей. Если для плоской фигуры S известны (рис. 20) скорость некоторой точки A и угловая скорость
Картина распределения скоростей точек плоской фигуры наглядно определяется, если найден её мгновенный центр скоростей (МЦС). Согласно теореме о МЦС, при непоступательном движении плоской фигуры (рис. 20) в каждый момент времени существует такая единственная точка P, скорость которой в данный момент времени равна нулю и которая называется мгновенным центром скоростей. Если для плоской фигуры S известны (рис. 20) скорость некоторой точки A и угловая скорость  , то для определения МЦС необходимо повернуть вектор
, то для определения МЦС необходимо повернуть вектор 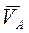 вокруг точки A на угол 90° в сторону круговой стрелки
вокруг точки A на угол 90° в сторону круговой стрелки  и на полученной при этом прямой AL отложить отрезок AP, равный
и на полученной при этом прямой AL отложить отрезок AP, равный
 , то скорости любых точек A и B фигуры равны
, то скорости любых точек A и B фигуры равны
 и
и  фигуры (рис. 24)
фигуры (рис. 24)  , то МЦС находится в
, то МЦС находится в  , тогда угловая скорость фигуры
, тогда угловая скорость фигуры
 любой точки
любой точки  плоской фигуры (рис. 25) равно геометрической сумме ускорения
плоской фигуры (рис. 25) равно геометрической сумме ускорения  точки А, принятой за полюс, вращательного
точки А, принятой за полюс, вращательного  и центростремительного
и центростремительного  ускорений при вращении точки
ускорений при вращении точки  вместе с фигурой вокруг полюса
вместе с фигурой вокруг полюса  :
:
 по равенству (2.24) находим и направляем ускорения
по равенству (2.24) находим и направляем ускорения  и
и  ,
,
 .
.
 Скорость
Скорость  направлена
направлена  в сторону
в сторону  .
.
 Пример 3. В планетарном механизме (рис. 29) колесо 2 катится без скольжения по неподвижному колесу и приводится в движение кривошипом
Пример 3. В планетарном механизме (рис. 29) колесо 2 катится без скольжения по неподвижному колесу и приводится в движение кривошипом  . Определить скорости и ускорения точек
. Определить скорости и ускорения точек  и
и 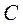 колеса 2 механизма, если
колеса 2 механизма, если
 ,
,

 м/с²;
м/с²;
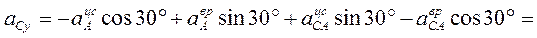
 м/с².
м/с².


 Все точки цилиндра A шатуна AB движутся в плоскостях, параллельных вертикальной плоскости.
Все точки цилиндра A шатуна AB движутся в плоскостях, параллельных вертикальной плоскости.


 При плоском движении тела прямые, проведенные в теле перпендикулярно плоскости параллелизма, движутся поступательно, поэтому для изучения плоского движения тела достаточно изучить движение плоской фигуры, которая получается при сечении тела плоскостью, параллельной плоскости параллелизма. Так, для изучения плоского движения цилиндра
При плоском движении тела прямые, проведенные в теле перпендикулярно плоскости параллелизма, движутся поступательно, поэтому для изучения плоского движения тела достаточно изучить движение плоской фигуры, которая получается при сечении тела плоскостью, параллельной плоскости параллелизма. Так, для изучения плоского движения цилиндра  и
и  некоторой её точки
некоторой её точки  и угол
и угол 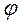 , характеризующий поворот подвижной системы отсчёта
, характеризующий поворот подвижной системы отсчёта 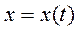 ,
, 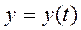 ,
,  (2.20)
(2.20) Между скоростями точек плоской фигуры существует зависимость, которая определяется теоремой: скорость любой точки
Между скоростями точек плоской фигуры существует зависимость, которая определяется теоремой: скорость любой точки  вращения точки
вращения точки  , а вектор
, а вектор  направлен
направлен  в сторону круговой стрелки
в сторону круговой стрелки  направлена по диагонали параллелограмма, построенного на векторах
направлена по диагонали параллелограмма, построенного на векторах  , получаем теорему о проекциях скоростей: проекции скоростей двух точек плоской фигуры на прямую, соединяющую эти точки, равны между собой.
, получаем теорему о проекциях скоростей: проекции скоростей двух точек плоской фигуры на прямую, соединяющую эти точки, равны между собой. . (2.22)
. (2.22) .
.
 . (2.23)
. (2.23) и
и  в сторону круговой стрелки
в сторону круговой стрелки  Из рисунка видно, что для определения МЦС в общем случае необходимо знать направление скоростей двух любых точек
Из рисунка видно, что для определения МЦС в общем случае необходимо знать направление скоростей двух любых точек 
 .
. 2. Если для двух точек
2. Если для двух точек  и
и  , то МЦС находится на пересечении прямой
, то МЦС находится на пересечении прямой 
 .
. В этом случае скорости всех точек фигуры одинаковы по модулю и направлению и фигура либо движется поступательно, либо происходит мгновенное распределение скоростей фигуры, как при поступательном движении.
В этом случае скорости всех точек фигуры одинаковы по модулю и направлению и фигура либо движется поступательно, либо происходит мгновенное распределение скоростей фигуры, как при поступательном движении.
 . (2.24)
. (2.24) , вектор
, вектор  , вектор
, вектор  .
. – ускорение при вращении точки
– ускорение при вращении точки  (рис. 25), причём
(рис. 25), причём и
и  . (2.25)
. (2.25) Аналогично МЦС для плоской фигуры при непоступательном её движении существует мгновенный центр ускорения (МЦУ).
Аналогично МЦС для плоской фигуры при непоступательном её движении существует мгновенный центр ускорения (МЦУ).  – это точка, ускорение которой в данный момент времени равно нулю. Если для плоской фигуры известны ускорение
– это точка, ускорение которой в данный момент времени равно нулю. Если для плоской фигуры известны ускорение  - определить угол
- определить угол  отложить отрезок
отложить отрезок  .
.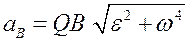 ,
,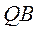 угол
угол  Пример 1. Отрезок
Пример 1. Отрезок 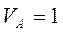 м/с,
м/с,  ,
,  м,
м,  и
и  находится на пересечении указанных перпендикуляров.
находится на пересечении указанных перпендикуляров. рад/с,
рад/с, м/с;
м/с;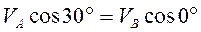 ,
, м/с.
м/с. м,
м,  м,
м, 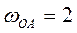 рад/с,
рад/с,  рад/с. Направление угловых скоростей
рад/с. Направление угловых скоростей 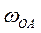 и
и  указано на рисунке.
указано на рисунке. совершают плоское движение. Поскольку направление скорости точки
совершают плоское движение. Поскольку направление скорости точки 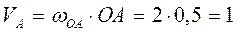 м/с;
м/с;  в сторону
в сторону  м/с;
м/с; 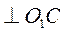 в сторону
в сторону  и
и  . (2.26)
. (2.26) . (2.27)
. (2.27) . Задаём направление указанных скоростей. Модули скоростей
. Задаём направление указанных скоростей. Модули скоростей  , откуда
, откуда 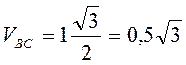 м/с.
м/с.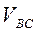 получилась со знаком «+», направление вектора
получилась со знаком «+», направление вектора 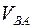 . Учитывая, что
. Учитывая, что  , находим:
, находим: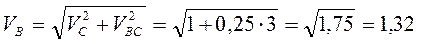 м/с.
м/с.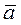 ,угловую скорость
,угловую скорость  м,
м, рад/с,
рад/с, рад/с²и кривошип
рад/с²и кривошип 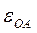 . Находим ускорение точки
. Находим ускорение точки  ,
, м/с²;
м/с²; 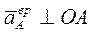 в сторону
в сторону  м/с²;
м/с²;  направлен по
направлен по 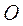 .
. м/с;
м/с;  в сторону
в сторону  рад/с,
рад/с, м/с;
м/с;  в сторону ω,
в сторону ω,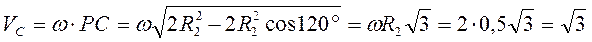 м/с;
м/с;  в сторону
в сторону  .
. рад/с².
рад/с².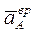 вращает колесо относительно МЦС – точки
вращает колесо относительно МЦС – точки  ,
, м/с²;
м/с²; 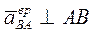 в сторону
в сторону  м/с²;
м/с²;  и
и 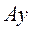 :
: м/с²;
м/с²; м/с².
м/с². м/с².
м/с². .
. м/с²;
м/с²;  в сторону
в сторону  направлен по СА от С к А.
направлен по СА от С к А. на оси
на оси  м/с².
м/с². м/с².
м/с². м/с².
м/с². Пример 4. Кривошип
Пример 4. Кривошип 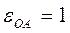 рад/с². Определить в заданном положении механизма скорость и ускорение точек
рад/с². Определить в заданном положении механизма скорость и ускорение точек  и
и  Звено
Звено 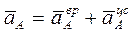 ,
, м/с²;
м/с²; 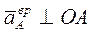 в сторону
в сторону  м/с²;
м/с²;  м/с;
м/с;  рад/с,
рад/с,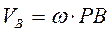 ;
;  м;
м;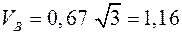 м/с;
м/с; ;
; м;
м; м/с.
м/с. в сторону
в сторону  . (2.28)
. (2.28) , зная которое определяем
, зная которое определяем 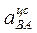
 м/с²;
м/с²;  направлено по
направлено по 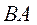 от
от  находим путём проектирования равенства на две любые оси. Оси следует выбирать так, чтобы на каждую проектировалось только одно неизвестное ускорение равенства (2.28).
находим путём проектирования равенства на две любые оси. Оси следует выбирать так, чтобы на каждую проектировалось только одно неизвестное ускорение равенства (2.28). , направленную по
, направленную по  ;
; м/с².
м/с².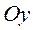
 м/с².
м/с². , находим угловое ускорение звена
, находим угловое ускорение звена 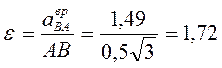 рад/с²,
рад/с²,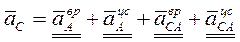 . (2.29)
. (2.29) м/с²;
м/с²;  м/с²;
м/с²; 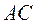 от
от  и
и  м/с².
м/с².