
|
|
Центр тяжести твёрдого тела
Тело А (рис. 64) находится в однородном поле сил тяготения. Разбиваем это тело на бесконечно малые тела
Точка С, в которой приложен вес тела
Согласно основному свойству центра параллельных сил, положение центра тяжести С относительно тела А не меняется при повороте тела в пространстве. Следовательно, центром тяжести тела называется точка С, в которой приложен вес тела Р и положение которой относительно тела не меняется при повороте тела в пространстве. Координаты центра тяжести С найдём, используя выражения (4.6) для координат центра параллельных сил:
В общем случае для определения координат центра тяжести тела используют выражения (4.7). Однако если тела однородные, то эти выражения можно упростить.
1. Однородный объём Обозначим через Тогда вес k-го элемента тела с объёмом
Подставляя значения Р, РК в выражения (4.7), получаем координаты центра тяжести однородного объёма:
где Если тело не разбивается на отдельные тела, координаты центров тяжести которых известны, то разбиваем тело на бесконечно малые объёмы
В выражениях (4.9) интегрирование осуществляется по всему объёму V. 2. Однородная площадь Совмещаем тело с плоскостью Oxy. В этом случае координата центра тяжести тела Пусть
Подставляя
Из выражений (4.10) получаем
Выражения (4.11) называются статическими моментами площади относительно осей Oy и Ox соответственно. Если начало отсчёта О системы осей Oxy совместить с центром тяжести – точкой С , то в этом случае координаты центра тяжести тела
Следовательно, статический момент площади относительно любой оси, проходящей через центр тяжести тела, равен нулю. Если плоское тело не разбивается на отдельные тела, координаты центров тяжести которых известны, то в этом случае по аналогии с выражениями (4.9) получаются выражения интегрального вида:
В выражениях (4.12) интегрирование проводится по площади тела S. 3. Однородная линия Разбиваем тело на ряд тел, координаты центров тяжести известны. Обозначим через
Подставляя значения
Если линия не разбивается на отдельные тела, координаты центров тяжести которых известны, то в этом случае по аналогии с выражениями (4.9) и (4.12) получаются интегральные выражения:
В выражениях (4.14) интегрирование осуществляется по всей длине линии L, т.е. это криволинейные интегралы. 4. Замечание о симметрии тела Пусть тело имеет плоскость симметрии, которую совмещаем с плоскостью Oxy (рис. 65). Ввиду симметрии каждому элементу тела vk с координатой zk (расположенному над плоскостью симметрии) соответствует такой же элемент vk с координатой zk, который расположен под плоскостью симметрии. В этом случае в выражениях (4.8) координата
1. Если тело имеет плоскость симметрии, его центр тяжести находится в этой плоскости. 2. Если тело имеет две плоскости симметрии, его центр тяжести находится на линии их пересечения. 3. Если тело имеет три плоскости симметрии, его центр тяжести находится в точке их пересечения. Рассмотрим примеры определения координат центров тяжести некоторых однородных тел.
Пример 1
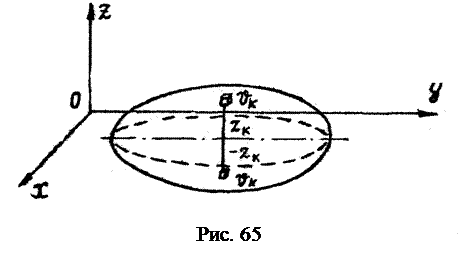
Совмещаем ось Ох (рис. 66) с осью симметрии дуги АВ. Тогда координата
Выделяем на центральном угле j бесконечно малую дугу dl с центральным углом
Подставляя эти значения в выражение (4.15), получаем:
Следовательно, координата
где a – половина центрального угла дуги в радианах.
Пример 2 Центр тяжести треугольника. Разбиваем треугольник (рис. 67) на бесконечно тонкие полоски, параллельные стороне АД. Так как полоски имеют бесконечно малую ширину, можно считать, что их центры тяжести находятся на середине длинных сторон полосок. Следовательно, центры тяжести таких полосок находятся на меридиане ВК.
При этом очевидны соотношения:
Пример 3 Центр тяжести однородного сектора с центральным углом 2a и радиусом R.
Выделяем из сектора элементар-ный сектор с бесконечно малым углом Используя выражение (4.16) для центра тяжести дуги, получаем координаты центра тяжести однородного сектора:
В выражении (4.17) α – половина центрального угла сектора, выражается в радианах.
Пример 4 Определить координаты центра тяжести однородного плоского тела (рис. 69), которое получается, если из квадрата 1 со стороны Задачу решаем методом отрицательных площадей.
1. Квадрат без выреза
2. Четверть круга с отрицательной площадью

3. Треугольник
Находим координаты центра тяжести тела
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что называется центром параллельных сил? Каково его основное свойство? 2. По каким формулам вычисляются координаты центра параллельных сил? 3. Что называется центром тяжести тела? 4. Как определяются координаты центра тяжести тела в общем случае? 5. По каким формулам вычисляются координаты центров тяжести однородных объёмных тел, плоских фигур и линий? 6. Что называется статическим моментом площади плоской фигуры относительно оси? Как он вычисляется? Какую размерность имеет? 7. В чём сущность метода отрицательных площадей при определении координат центров тяжести плоских тел? РАЗДЕЛ II. КИНЕМАТИКА
Во втором разделе пособия излагаются основные положения теории кинематики и методика решения задач по кинематике. Как и в первом разделе пособия "Статика", в разделе «Кинематика» объём изложенной в пособии теории соответствует тому объёму знаний по кинематике, который должны иметь студенты для решения задач и выполнения расчётно-графических работ по данному разделу, поэтому основные теоремы кинематики излагаются без вывода и даются пояснения по практическому применению этих теорем. Некоторые разделы кинематики излагаются в пособии достаточно подробно и могут быть рекомендованы для самостоятельного изучения. Кинематика – раздел теоретической механики, в котором изучается движение материальных объектов без учёта их масс и действующих на них сил. В нём изучается простейшая форма движения материи – механическое движение, то есть происходящее во времени изменение положения одного материального объекта относительно другого, с которым связывается система отсчёта. В кинематике рассматриваются две основные задачи. Первая задача – установление закона движения объекта, т.е. такого математического описания движения, которое определяет положение движущегося объекта в пространстве. Вторая задача – определение по известному закону движения объекта основных кинематических характеристик движения. В зависимости от вида рассматриваемых объектов различают кинематику точки, кинематику твёрдого тела и кинематику сплошной среды.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
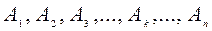 , вес которых соответственно равен
, вес которых соответственно равен  . Отсюда следует, что на тело действует система параллельных сил. Равнодействующая этой системы сил есть вес тела
. Отсюда следует, что на тело действует система параллельных сил. Равнодействующая этой системы сил есть вес тела .
.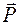 , называется центром тяжести тела.
, называется центром тяжести тела.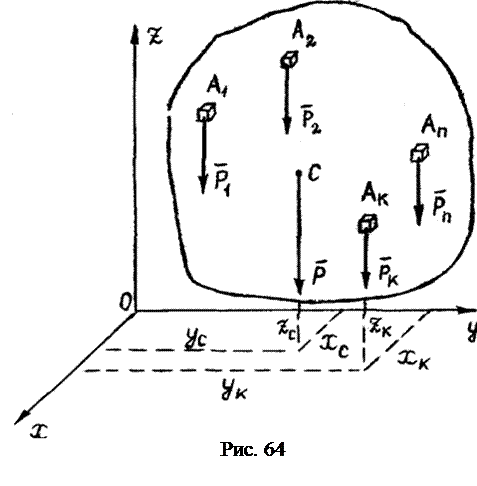
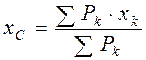 ,
, 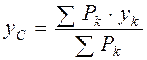 ,
, 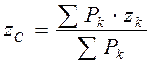 . (4.7)
. (4.7) вес единицы объёма тела (удельный вес).
вес единицы объёма тела (удельный вес). равен
равен 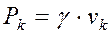 . Вес тела объёмом V равен
. Вес тела объёмом V равен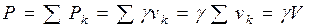 .
. ,
, 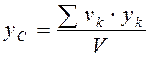 ,
, 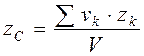 , (4.8)
, (4.8) – координаты центра тяжести k-го тела объёмом
– координаты центра тяжести k-го тела объёмом 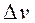 и, переходя в выражениях (4.8) к пределу при
и, переходя в выражениях (4.8) к пределу при 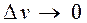 , получаем выражение (4.9):
, получаем выражение (4.9): . (4.9)
. (4.9)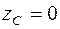 .
. – вес единицы площади тела. Вес k-го элемента тела площадью
– вес единицы площади тела. Вес k-го элемента тела площадью  равен
равен 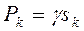 , вес тела площадью S равен
, вес тела площадью S равен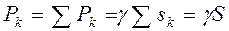 .
.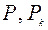 в выражения (4.7), получаем координаты центра тяжести однородного плоского тела:
в выражения (4.7), получаем координаты центра тяжести однородного плоского тела: ,
,  . (4.10)
. (4.10) ,
, 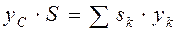 . (4.11)
. (4.11)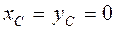 . Из выражений (4.11) следует, что в этом случае статические моменты тела равны 0:
. Из выражений (4.11) следует, что в этом случае статические моменты тела равны 0: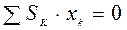 ,
,  .
. . (4.12)
. (4.12) вес единицы длины тела. Тогда вес
вес единицы длины тела. Тогда вес  тела длиной lk равен
тела длиной lk равен  , вес тела длиной L равен
, вес тела длиной L равен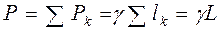 .
.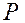 ,
, 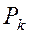 в выражения (4.7), получаем после сокращения на
в выражения (4.7), получаем после сокращения на 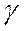 координаты центров тяжести однородной линии:
координаты центров тяжести однородной линии: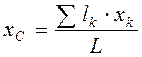 ,
, 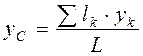 ,
, 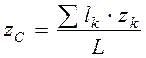 . (4.13)
. (4.13)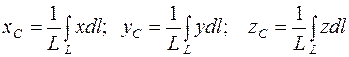 . (4.14)
. (4.14)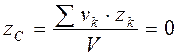 .
. Следовательно:
Следовательно: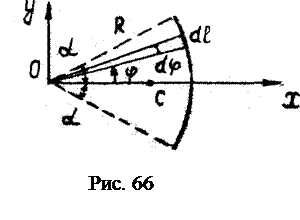 Центр тяжести однородной дуги радиусом R и центральным углом 2a.
Центр тяжести однородной дуги радиусом R и центральным углом 2a.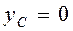 . Для определе-ния координаты
. Для определе-ния координаты 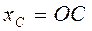 воспользуемся выражением из формулы (4.14)
воспользуемся выражением из формулы (4.14)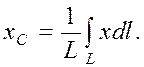 (4.16)
(4.16) . Тогда
. Тогда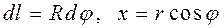 и длина дуги
и длина дуги  .
.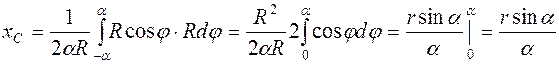 .
. центра тяжести однородной дуги определяется выражением
центра тяжести однородной дуги определяется выражением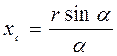 , (4.16)
, (4.16)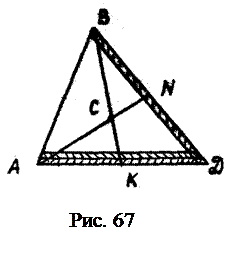 Разбивая треугольник на тонкие полоски параллельные стороне ВД, получим, что их центры тяжести лежат на медиане AN. Следовательно, центр тяжести треугольника C находится в точке пересечения его медиан.
Разбивая треугольник на тонкие полоски параллельные стороне ВД, получим, что их центры тяжести лежат на медиане AN. Следовательно, центр тяжести треугольника C находится в точке пересечения его медиан.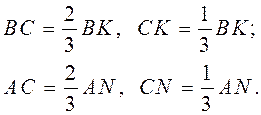
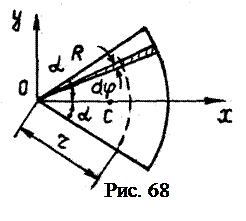 Сектор (рис. 68) симметричен относительно биссектрисы централь-ного угла, с которой совмещаема ось Ox. В этом случае координата
Сектор (рис. 68) симметричен относительно биссектрисы централь-ного угла, с которой совмещаема ось Ox. В этом случае координата  .
.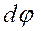 . Этот элементарный сектор можно считать треугольником, центр тяжести которого находится на расстоянии
. Этот элементарный сектор можно считать треугольником, центр тяжести которого находится на расстоянии 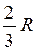 , поэтому центры тяжести элементарных секторов находятся на дуге
, поэтому центры тяжести элементарных секторов находятся на дуге 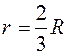 .
.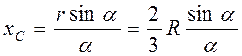 . (4.17)
. (4.17)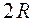 вырезана четвёртая часть круга 2 радиусом R и присоединён треугольник 3.
вырезана четвёртая часть круга 2 радиусом R и присоединён треугольник 3.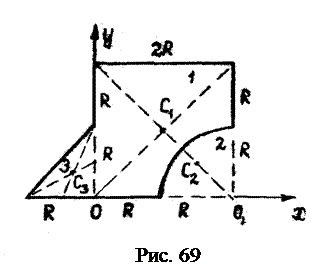 Разбиваем тело на три элемента. Определяем площадь и координаты центров тяжести каждого элемента.
Разбиваем тело на три элемента. Определяем площадь и координаты центров тяжести каждого элемента.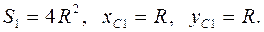
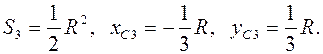
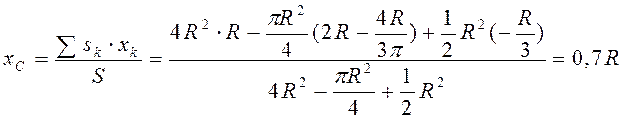 ;
;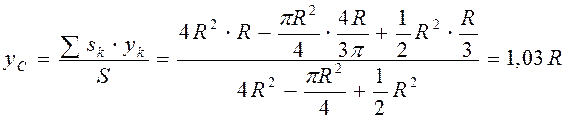 .
.