ГЛАВА 2. Моменты сил относительно точки
И ОСИ. ПАРА СИЛ. ПРОСТРАНСТВЕННАЯ И ПЛОСКАЯ
ПРОИЗВОЛЬНЫЕ СИСТЕМЫ СИЛ
В главе даны понятия моментов силы относительно точки и оси, изложены основные положения теории и методики решения задач на плоскую и пространственную систему сил.
Момент силы относительно точки
Моментом силы  относительно некоторой точки О называют скалярную величину, равную взятому с соответствующим знаком произведению модуля силы относительно некоторой точки О называют скалярную величину, равную взятому с соответствующим знаком произведению модуля силы 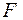 на плечо h (рис. 23): на плечо h (рис. 23):
 (2.1) (2.1)
 Момент Момент  имеет знак "+", если сила имеет знак "+", если сила  вращает тело относительно точки 0 против хода часовой стрелки, "-" – по ходу часовой стрелки. вращает тело относительно точки 0 против хода часовой стрелки, "-" – по ходу часовой стрелки.
Точка О, относительно которой находится момент, называется моментной точкой.
Плечом h силы  относительно моментной точки О называется перпендикуляр, опущенный из точки О на линию действия силы относительно моментной точки О называется перпендикуляр, опущенный из точки О на линию действия силы  . .
Свойства момента силы относительно точки:
1)  не меняется при переносе силы вдоль её линии действия; не меняется при переносе силы вдоль её линии действия;
2)  , если h = 0, т.е. если моментная точка О находится на линии действия силы; , если h = 0, т.е. если моментная точка О находится на линии действия силы;
3)  численно равен удвоенной площади треугольника ОАВ, основание которого – сила численно равен удвоенной площади треугольника ОАВ, основание которого – сила  , а вершина – моментная точка О (заштрихован на рис. 25): , а вершина – моментная точка О (заштрихован на рис. 25):
 . .
Момент силы измеряется в системе СИ в ньютон-метрах (Н·м). При определении момента силы относительно точки в задачах часто удобно силу  разложить на её составляющие по осям Ox и Oy и отдельно найти момент каждой составляющей относительно той же моментной точки. Справедливость такого способа определения момента вытекает из теоремы Вариньона о моменте равнодействующей. При разложении силы на составляющие необходимо, чтобы каждая из них была приложена в той же точке, что и сила разложить на её составляющие по осям Ox и Oy и отдельно найти момент каждой составляющей относительно той же моментной точки. Справедливость такого способа определения момента вытекает из теоремы Вариньона о моменте равнодействующей. При разложении силы на составляющие необходимо, чтобы каждая из них была приложена в той же точке, что и сила  . .
  Найдём, например, момент силы Найдём, например, момент силы  относительно точки А (рис. 24), если АВ = 0,3 м, ВС = 0,5 и α = 60°, F = 10 Н. По определению момента силы относительно точки относительно точки А (рис. 24), если АВ = 0,3 м, ВС = 0,5 и α = 60°, F = 10 Н. По определению момента силы относительно точки  Поскольку плечо силы определять в данной задаче неудобно, представим силу Поскольку плечо силы определять в данной задаче неудобно, представим силу  в виде в виде  , где , где  , ,  – соответственно горизонтальная и вертикальная составляющие, приложенные в той же точке С, что и сила – соответственно горизонтальная и вертикальная составляющие, приложенные в той же точке С, что и сила  . Тогда плечо силы . Тогда плечо силы  относительно точки А равно AB, силы относительно точки А равно AB, силы 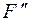 – ВС. – ВС.

Момент силы относительно точки как вектор
 Момент силы Момент силы  относительно точки О можно представить в виде вектора относительно точки О можно представить в виде вектора  . .
Вектор  (рис. 25) приложен в моментной точке О перпендикулярно плоскости, проходящей через линию действия силы и моментную точку О (плоскость ОАВ на рис. 25), и направляется в ту сторону, откуда вращение тела под действием силы (рис. 25) приложен в моментной точке О перпендикулярно плоскости, проходящей через линию действия силы и моментную точку О (плоскость ОАВ на рис. 25), и направляется в ту сторону, откуда вращение тела под действием силы  относительно точки О представляется происходящим против хода часовой стрелки. Модуль вектора относительно точки О представляется происходящим против хода часовой стрелки. Модуль вектора  равен моменту силы равен моменту силы  относительно точки О: относительно точки О:
 . (2.2) . (2.2)
Справедливо следующее векторное равенство:
 (2.3) (2.3)
где  – радиус-вектор, проведенный из моментной точки О в точку А приложения силы – радиус-вектор, проведенный из моментной точки О в точку А приложения силы  . .
Из векторного равенства (2.3) можно определить модуль (2.2) и указанное направление вектора  . .
Момент силы относительно оси
Момент силы  относительно некоторой оси z относительно некоторой оси z  равен моменту проекции этой силы на любую плоскость, перпендикулярную оси z (например, плоскость Оху на рис. 26), относительно точки встречи оси с плоскостью – точки О: равен моменту проекции этой силы на любую плоскость, перпендикулярную оси z (например, плоскость Оху на рис. 26), относительно точки встречи оси с плоскостью – точки О:

где  – проекция силы – проекция силы  на плоскость Охy, перпендикулярную оси z (рис. 26). на плоскость Охy, перпендикулярную оси z (рис. 26).
 Момент силы относительно оси Момент силы относительно оси  считается положительным, если вращение тела силой считается положительным, если вращение тела силой  происходит против хода часовой стрелки, и отрицательным, если она стремится вращать тело по ходу часовой стрелки (если смотреть на тело с положительного направления оси Оz). происходит против хода часовой стрелки, и отрицательным, если она стремится вращать тело по ходу часовой стрелки (если смотреть на тело с положительного направления оси Оz).
Из определения момента силы относительно оси следует:
1)  , если сила , если сила  параллельна оси (так, на рис. 26 составляющая параллельна оси (так, на рис. 26 составляющая  силы F момента относительно этой оси не даёт); силы F момента относительно этой оси не даёт);
2)  , если линия действия силы , если линия действия силы  пересекает ось Oz. пересекает ось Oz.
Объединяя эти два свойства, можно сказать, что  , если сила , если сила  и ось Oz находятся в одной плоскости. и ось Oz находятся в одной плоскости.
Пример
 По диагонали KN (рис. 27) параллелепипеда, размеры которого указаны на рис. 27, действует сила F = 10 Н. Найти моменты этой силы относительно координатных осей. По диагонали KN (рис. 27) параллелепипеда, размеры которого указаны на рис. 27, действует сила F = 10 Н. Найти моменты этой силы относительно координатных осей.
Решение
Для определения момента силы  относительно оси Ох вектор силы проектируем на плоскость Oyz, перпендикулярную оси, получаем относительно оси Ох вектор силы проектируем на плоскость Oyz, перпендикулярную оси, получаем  и находим момент составляющей и находим момент составляющей  относительно точки О – точки встречи оси Ox с плоскостью Oух относительно точки О – точки встречи оси Ox с плоскостью Oух
 (H×м). (H×м).
Знак "минус" момента взят потому, что сила  вращает тело относительно точки О по часовой стрелке, если смотреть на тело с положительного направления оси Ox. вращает тело относительно точки О по часовой стрелке, если смотреть на тело с положительного направления оси Ox.
Момент силы  относительно оси Oy относительно оси Oy  , так как сила , так как сила  пересекает ось Оу. пересекает ось Оу.
Для определения момента силы  относительно оси Oz вектор силы проектируем на плоскость Oxy, перпендикулярную оси Oz, получаем относительно оси Oz вектор силы проектируем на плоскость Oxy, перпендикулярную оси Oz, получаем  и находим момент составляющей и находим момент составляющей  относительно точки О – точки встречи оси Oz с плоскостью Oxy относительно точки О – точки встречи оси Oz с плоскостью Oxy
 (Н×м). (Н×м).
Знак "плюс" момента взят потому, что сила  вращает тело относительно точки O против хода часовой стрелки, если смотреть на тело с положительного направления оси Oz. вращает тело относительно точки O против хода часовой стрелки, если смотреть на тело с положительного направления оси Oz.
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


 относительно некоторой точки О называют скалярную величину, равную взятому с соответствующим знаком произведению модуля силы
относительно некоторой точки О называют скалярную величину, равную взятому с соответствующим знаком произведению модуля силы 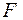 на плечо h (рис. 23):
на плечо h (рис. 23): (2.1)
(2.1) Момент
Момент  имеет знак "+", если сила
имеет знак "+", если сила  , если h = 0, т.е. если моментная точка О находится на линии действия силы;
, если h = 0, т.е. если моментная точка О находится на линии действия силы; .
.
 Найдём, например, момент силы
Найдём, например, момент силы  Поскольку плечо силы определять в данной задаче неудобно, представим силу
Поскольку плечо силы определять в данной задаче неудобно, представим силу  , где
, где  ,
,  – соответственно горизонтальная и вертикальная составляющие, приложенные в той же точке С, что и сила
– соответственно горизонтальная и вертикальная составляющие, приложенные в той же точке С, что и сила  относительно точки А равно AB, силы
относительно точки А равно AB, силы 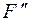 – ВС.
– ВС.
 Момент силы
Момент силы  .
. . (2.2)
. (2.2) (2.3)
(2.3) – радиус-вектор, проведенный из моментной точки О в точку А приложения силы
– радиус-вектор, проведенный из моментной точки О в точку А приложения силы  равен моменту проекции этой силы на любую плоскость, перпендикулярную оси z (например, плоскость Оху на рис. 26), относительно точки встречи оси с плоскостью – точки О:
равен моменту проекции этой силы на любую плоскость, перпендикулярную оси z (например, плоскость Оху на рис. 26), относительно точки встречи оси с плоскостью – точки О:
 – проекция силы
– проекция силы  Момент силы относительно оси
Момент силы относительно оси  происходит против хода часовой стрелки, и отрицательным, если она стремится вращать тело по ходу часовой стрелки (если смотреть на тело с положительного направления оси Оz).
происходит против хода часовой стрелки, и отрицательным, если она стремится вращать тело по ходу часовой стрелки (если смотреть на тело с положительного направления оси Оz). , если сила
, если сила  силы F момента относительно этой оси не даёт);
силы F момента относительно этой оси не даёт); По диагонали KN (рис. 27) параллелепипеда, размеры которого указаны на рис. 27, действует сила F = 10 Н. Найти моменты этой силы относительно координатных осей.
По диагонали KN (рис. 27) параллелепипеда, размеры которого указаны на рис. 27, действует сила F = 10 Н. Найти моменты этой силы относительно координатных осей. и находим момент составляющей
и находим момент составляющей  относительно точки О – точки встречи оси Ox с плоскостью Oух
относительно точки О – точки встречи оси Ox с плоскостью Oух (H×м).
(H×м). , так как сила
, так как сила  и находим момент составляющей
и находим момент составляющей  относительно точки О – точки встречи оси Oz с плоскостью Oxy
относительно точки О – точки встречи оси Oz с плоскостью Oxy (Н×м).
(Н×м).