Уравновешенной системы сил
Действие системы сил на абсолютно твёрдое тело не изменится, если к ней присоединить или отбросить систему сил, эквивалентную нулю.
Следствие из аксиомы 3: действие данной силы на абсолютно твёрдое тело не изменится при переносе силы вдоль ее линии действия из точки А в точку В (рис. 2), т.е. в статике твёрдого тела сила – вектор скользящий.
4. Аксиома параллелограмма
 Равнодействующая двух пересекающихся сил проходит через точку их пересечения и определяется диагональю параллелограмма, построенного на этих силах как на сторонах (рис. 3). Равнодействующая двух пересекающихся сил проходит через точку их пересечения и определяется диагональю параллелограмма, построенного на этих силах как на сторонах (рис. 3).
Правило параллелограмма даёт геометрический способ определения равнодействующих двух пересекающихся сил:
 . .
Модуль равнодействующей можно определить, например, по теореме косинусов
 ; ;
но  , ,
откуда  . .
5. Аксиома равенства действия и противодействия
 Два материальных тела действуют друг на друга с силами, равными по модулю и направленными по одной прямой в противоположные стороны (рис. 4). Согласно аксиоме действия и противодействия, силы Два материальных тела действуют друг на друга с силами, равными по модулю и направленными по одной прямой в противоположные стороны (рис. 4). Согласно аксиоме действия и противодействия, силы  . Однако система сил . Однако система сил  не является уравновешенной, так как силы приложены к разным телам. не является уравновешенной, так как силы приложены к разным телам.
6. Аксиома затвердевания
Равновесие деформированного тела под действием данной системы сил не изменится, если тело затвердеет (станет абсолютно твёрдым). Так, равновесие цепи не нарушится, если звенья цепи приварить друг к другу.
7. Аксиома отбрасывания связей (принцип освобождаемости)
Твёрдое тело называется свободным, если оно может перемещаться в любом направлении пространства.
Тела, ограничивающие свободу перемещения данного тела и делающие его несвободным, называются связями. В связях под действием приложенных к телу сил (активных сил) возникают усилия, называемые реакциями связей.
Согласно принципу освобождаемости от связей, несвободное твёрдое тело можно рассматривать как свободное, если освободиться от связей, а их действие на тело заменить реакциями связей.
Рассмотрим наиболее часто встречаемые в задачах статики связи и возникающие в них реакции связей.
1. Гладкая (идеальная) поверхность (поверхность без трения)
Реакция  такой поверхности (рис. 5а) направлена по общей нормали к соприкасающимся поверхностям. такой поверхности (рис. 5а) направлена по общей нормали к соприкасающимся поверхностям.
 Если одна из поверхностей обращается в точку (рис. 5б), то реакция Если одна из поверхностей обращается в точку (рис. 5б), то реакция  направлена по нормали ко второй поверхности. Отсюда следует, что реакция цилиндрической подвижной (катковой) опоры А направлена по нормали ко второй поверхности. Отсюда следует, что реакция цилиндрической подвижной (катковой) опоры А 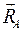 (рис. 6а) направлена по нормали к опорной поверхности. Иногда в задачах катковую опору изображают в виде "салазок" (рис. 6б). (рис. 6а) направлена по нормали к опорной поверхности. Иногда в задачах катковую опору изображают в виде "салазок" (рис. 6б).
2. Гибкая нить
Реакция гибкой нити  направлена по нити к точке подвеса (рис. 7). направлена по нити к точке подвеса (рис. 7).
3. Цилиндрический шарнир
 Эта связь не препятствует повороту тела в плоскости Оху, перпендикулярной оси шарнира (рис. 8а), но препятствует радиальному перемещению тела. В задачах обозначается, как показано на рис. 8б. Эта связь не препятствует повороту тела в плоскости Оху, перпендикулярной оси шарнира (рис. 8а), но препятствует радиальному перемещению тела. В задачах обозначается, как показано на рис. 8б.
Реакция  цилиндрического шарнира может иметь любое направление в плоскости, и неизвестными являются модуль цилиндрического шарнира может иметь любое направление в плоскости, и неизвестными являются модуль  и угол и угол  ,характеризующий направление её линии действия. Обычно вместо ,характеризующий направление её линии действия. Обычно вместо  и и  рассматривают рассматривают  и и  – составляющие реакции – составляющие реакции  поосям координат. поосям координат.
4. Сферический (пространственный) шарнир
 Сферический шарнир не препятствует повороту тела в пространстве (рис. 9а), в задачах обозначается так же, как и цилиндрический шарнир (рис. 9б). Сферический шарнир не препятствует повороту тела в пространстве (рис. 9а), в задачах обозначается так же, как и цилиндрический шарнир (рис. 9б).
Реакция  сферического шарнира может иметь любое направление в пространстве, и неизвестными являются её модуль R и два утла сферического шарнира может иметь любое направление в пространстве, и неизвестными являются её модуль R и два утла  и и  её наклона к осям Ох, Оу. Обычно вместо этих неизвестных вводят три составляющие её наклона к осям Ох, Оу. Обычно вместо этих неизвестных вводят три составляющие  , ,  и и  реакции реакции  по координатным осям. по координатным осям.
5. Подпятник
В подпятнике (рис. 10), как и в сферическом шарнире, неизвестными являются три составляющие реакции  по осям координат: по осям координат:  , ,  и и 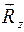 . .
6. Невесомый стержень с шарнирами на концах
  Реакция такого стержня СВ (рис. 11а) Реакция такого стержня СВ (рис. 11а)  направлена по стержню. Причём, если реакции стержня на узлы направлены к узлам, значит, со стороны узлов действуют сжимающие силы направлена по стержню. Причём, если реакции стержня на узлы направлены к узлам, значит, со стороны узлов действуют сжимающие силы  – стержень работает на сжатие (рис. 11б), если реакции направлены от узлов – на растяжение (рис. 11в). – стержень работает на сжатие (рис. 11б), если реакции направлены от узлов – на растяжение (рис. 11в).
7. Плоская заделка
Если действующие на балку АВ (рис. 12) силы  расположены в плоскости балки (плоскость чертежа), в этом случае А – плоская заделка. расположены в плоскости балки (плоскость чертежа), в этом случае А – плоская заделка.
В плоской заделке – три неизвестных: две составляющие  , ,  реакции на оси координат и пара с моментом реакции на оси координат и пара с моментом  . .
 8. Пространственная заделка 8. Пространственная заделка
 Если действующие на балку АВ силы Если действующие на балку АВ силы  имеют произвольное направление в пространстве, в этом случае А – пространственная заделка (рис. 13). В пространственной заделке шесть неизвестных: три составляющие имеют произвольное направление в пространстве, в этом случае А – пространственная заделка (рис. 13). В пространственной заделке шесть неизвестных: три составляющие  , ,  и и 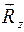 реакции на оси координат и три пары относительно координатных осей с моментами реакции на оси координат и три пары относительно координатных осей с моментами  . .
9. Скользящая опора
Для бруса AB связь A – скользящая опора (рис. 14). В опоре A две неизвестных: реакция  и момент и момент  . .
Система сходящихся сил
Сходящейся называется такая система сил, в которой линии действия всех сил пересекаются в одной точке (например, в точке О на рис. 15).
 Могут быть плоская и пространственная системы сходящихся сил. Могут быть плоская и пространственная системы сходящихся сил.
На тело действует пространственная система сходящихся сил  . Силы приложены соответственно в точках . Силы приложены соответственно в точках  , и их линии действия пересекаются в точке О. , и их линии действия пересекаются в точке О.
Перенося силы вдоль их линий действия в точку О, получим систему сил, приложенных в точке.
Используя правило параллелограмма, геометрически суммируем силы, приложенные в точке О. В результате получаем, что сходящуюся систему сил можно заменить одной силой, равной геометрической сумме всех сил, приложенных в точке О, – равнодействующей  : :
 . (1.1) . (1.1)
Правило параллелограмма для геометрического определения равнодействующей  применять неудобно из-за громоздкости построений, наносимых на основной чертёж. Для этого используется правило силового многоугольника. применять неудобно из-за громоздкости построений, наносимых на основной чертёж. Для этого используется правило силового многоугольника.
 Вне основного чертежа (рис. 16) выбираем произвольную точку О1 и в этой точке прикладываем силу Вне основного чертежа (рис. 16) выбираем произвольную точку О1 и в этой точке прикладываем силу  , геометрически равную силе , геометрически равную силе  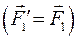 . К концу силы . К концу силы  прикладываем силу прикладываем силу   и т.д. до последней силы и т.д. до последней силы 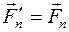 . .
Соединяя точку О с концом силы  , получим силу , получим силу  , равную геометрической сумме всех сил и называемую главным вектором данной системы сил. , равную геометрической сумме всех сил и называемую главным вектором данной системы сил.
 . (1.2) . (1.2)
Перенося  в точку О (рис. 15), получим равнодействующую в точку О (рис. 15), получим равнодействующую  данной системы сходящихся сил. данной системы сходящихся сил.
Правило силового многоугольника можно рассматривать как многократное применение правила параллелограмма (рис. 16).
Для равновесия сходящейся системы сил необходимо и достаточно, чтобы её равнодействующая  равнялась нулю: равнялась нулю:
 . (1.3) . (1.3)
Геометрически условие (1.3) выражается в замкнутости силового многоугольника – конец последней силы  совпадает с началом первой совпадает с началом первой  (с точкой О1 на рис. 17). (с точкой О1 на рис. 17).
 Аналитические условия равновесия пространственной системы сходящихся сил (1.4) получаем, спроектировав векторное равенство (1.3) на три координатные оси: Аналитические условия равновесия пространственной системы сходящихся сил (1.4) получаем, спроектировав векторное равенство (1.3) на три координатные оси:
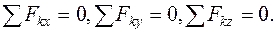 (1.4) (1.4)
Для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы суммы их проекций на три координатные оси равнялись нулю.
Аналитические условия равновесия плоской системы сходящихся сил определяются двумя уравнениями:
 . (1.5) . (1.5)
Для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы суммы их проекций на две координатные оси равнялись нулю.
Теорема о трёх силах
 Если тело находится в равновесии под действием трёх сил и линии действия двух сил (например, Если тело находится в равновесии под действием трёх сил и линии действия двух сил (например,  и и 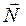 на рис. 18) пересекаются, то все силы лежат в одной плоскости и их линии действия пересекаются в одной точке. на рис. 18) пересекаются, то все силы лежат в одной плоскости и их линии действия пересекаются в одной точке.
На рис. 18 однородный шар весом Р подвешен на нити ВС и в точке А опирается на идеальную вертикальную поверхность.
Так как реакция 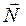 поверхности горизонтальна, то силы поверхности горизонтальна, то силы  и и 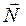 пересекаются в точке О. Согласно теореме о трёх силах, реакция нити пересекаются в точке О. Согласно теореме о трёх силах, реакция нити  должна проходить через точку О, поэтому на рис. 18 нить ВС должна совпадать с направлением ОС. должна проходить через точку О, поэтому на рис. 18 нить ВС должна совпадать с направлением ОС.
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


 Равнодействующая двух пересекающихся сил проходит через точку их пересечения и определяется диагональю параллелограмма, построенного на этих силах как на сторонах (рис. 3).
Равнодействующая двух пересекающихся сил проходит через точку их пересечения и определяется диагональю параллелограмма, построенного на этих силах как на сторонах (рис. 3). .
. ;
; ,
, .
. Два материальных тела действуют друг на друга с силами, равными по модулю и направленными по одной прямой в противоположные стороны (рис. 4). Согласно аксиоме действия и противодействия, силы
Два материальных тела действуют друг на друга с силами, равными по модулю и направленными по одной прямой в противоположные стороны (рис. 4). Согласно аксиоме действия и противодействия, силы  . Однако система сил
. Однако система сил  не является уравновешенной, так как силы приложены к разным телам.
не является уравновешенной, так как силы приложены к разным телам. такой поверхности (рис. 5а) направлена по общей нормали к соприкасающимся поверхностям.
такой поверхности (рис. 5а) направлена по общей нормали к соприкасающимся поверхностям. Если одна из поверхностей обращается в точку (рис. 5б), то реакция
Если одна из поверхностей обращается в точку (рис. 5б), то реакция  направлена по нормали ко второй поверхности. Отсюда следует, что реакция цилиндрической подвижной (катковой) опоры А
направлена по нормали ко второй поверхности. Отсюда следует, что реакция цилиндрической подвижной (катковой) опоры А 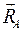 (рис. 6а) направлена по нормали к опорной поверхности. Иногда в задачах катковую опору изображают в виде "салазок" (рис. 6б).
(рис. 6а) направлена по нормали к опорной поверхности. Иногда в задачах катковую опору изображают в виде "салазок" (рис. 6б). направлена по нити к точке подвеса (рис. 7).
направлена по нити к точке подвеса (рис. 7). Эта связь не препятствует повороту тела в плоскости Оху, перпендикулярной оси шарнира (рис. 8а), но препятствует радиальному перемещению тела. В задачах обозначается, как показано на рис. 8б.
Эта связь не препятствует повороту тела в плоскости Оху, перпендикулярной оси шарнира (рис. 8а), но препятствует радиальному перемещению тела. В задачах обозначается, как показано на рис. 8б. цилиндрического шарнира может иметь любое направление в плоскости, и неизвестными являются модуль
цилиндрического шарнира может иметь любое направление в плоскости, и неизвестными являются модуль  и угол
и угол  ,характеризующий направление её линии действия. Обычно вместо
,характеризующий направление её линии действия. Обычно вместо  и
и  – составляющие реакции
– составляющие реакции  Сферический шарнир не препятствует повороту тела в пространстве (рис. 9а), в задачах обозначается так же, как и цилиндрический шарнир (рис. 9б).
Сферический шарнир не препятствует повороту тела в пространстве (рис. 9а), в задачах обозначается так же, как и цилиндрический шарнир (рис. 9б). её наклона к осям Ох, Оу. Обычно вместо этих неизвестных вводят три составляющие
её наклона к осям Ох, Оу. Обычно вместо этих неизвестных вводят три составляющие  реакции
реакции  ,
,  и
и 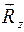 .
.
 Реакция такого стержня СВ (рис. 11а)
Реакция такого стержня СВ (рис. 11а)  – стержень работает на сжатие (рис. 11б), если реакции направлены от узлов – на растяжение (рис. 11в).
– стержень работает на сжатие (рис. 11б), если реакции направлены от узлов – на растяжение (рис. 11в). расположены в плоскости балки (плоскость чертежа), в этом случае А – плоская заделка.
расположены в плоскости балки (плоскость чертежа), в этом случае А – плоская заделка. .
. 8. Пространственная заделка
8. Пространственная заделка Если действующие на балку АВ силы
Если действующие на балку АВ силы  .
. и момент
и момент  Могут быть плоская и пространственная системы сходящихся сил.
Могут быть плоская и пространственная системы сходящихся сил. . Силы приложены соответственно в точках
. Силы приложены соответственно в точках  , и их линии действия пересекаются в точке О.
, и их линии действия пересекаются в точке О. :
: . (1.1)
. (1.1) Вне основного чертежа (рис. 16) выбираем произвольную точку О1 и в этой точке прикладываем силу
Вне основного чертежа (рис. 16) выбираем произвольную точку О1 и в этой точке прикладываем силу  , геометрически равную силе
, геометрически равную силе 
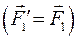 . К концу силы
. К концу силы 
 и т.д. до последней силы
и т.д. до последней силы 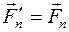 .
. , получим силу
, получим силу  , равную геометрической сумме всех сил и называемую главным вектором данной системы сил.
, равную геометрической сумме всех сил и называемую главным вектором данной системы сил. . (1.2)
. (1.2) . (1.3)
. (1.3) совпадает с началом первой
совпадает с началом первой  (с точкой О1 на рис. 17).
(с точкой О1 на рис. 17). Аналитические условия равновесия пространственной системы сходящихся сил (1.4) получаем, спроектировав векторное равенство (1.3) на три координатные оси:
Аналитические условия равновесия пространственной системы сходящихся сил (1.4) получаем, спроектировав векторное равенство (1.3) на три координатные оси: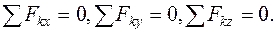 (1.4)
(1.4) . (1.5)
. (1.5) Если тело находится в равновесии под действием трёх сил и линии действия двух сил (например,
Если тело находится в равновесии под действием трёх сил и линии действия двух сил (например,  и
и 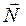 на рис. 18) пересекаются, то все силы лежат в одной плоскости и их линии действия пересекаются в одной точке.
на рис. 18) пересекаются, то все силы лежат в одной плоскости и их линии действия пересекаются в одной точке. должна проходить через точку О, поэтому на рис. 18 нить ВС должна совпадать с направлением ОС.
должна проходить через точку О, поэтому на рис. 18 нить ВС должна совпадать с направлением ОС.