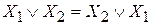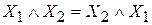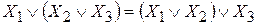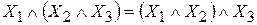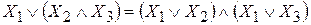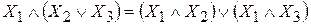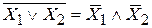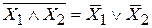|
|
Прямой, обратный и дополнительный коды и их использование при выполнении арифметических операцийВ большинстве компьютеров с целью упрощения конструкции АЛУ операция вычитания не используется. Она заменяется операцией сложения путем замены знака вычитаемого на противоположный и прибавления его к уменьшаемому:
В связи с этим для машинного изображения отрицательных чисел используют прямой, дополнительный и обратный коды. Положительные числа в прямом, обратном и дополнительном кодах изображаются одинаково – двоичными кодами с цифрой 0 в знаковом разряде (см., например, рис. 2.8в). Отрицательные числа в прямом, обратном и дополнительном кодах имеют разное изображение. Рассмотрим эти коды и их применение на примере отрицательных чисел, представленных в форме с фиксированной запятой. 1. Прямой код числа получается, если в знаковый разряд поместить цифру 1, а в разряды числовой части числа - двоичный код его абсолютной величины. 2. Обратный код получается инвертированием (заменой на обратные значения) всех цифр двоичного кода абсолютной величины числа, включая разряд знака: нули заменяются единицами, а единицы – нулями. Пример. Число: -1 Код модуля числа (в однобайтовом формате) 0,0000001 Обратный код 1,1111110 Представление числа в разрядной сетке показано на рис. 2.10
Рис. 2.10. Пример. Число –127 Код модуля числа 0,1111111 Обратный код числа 1,0000000. Представление числа в обратном коде показано на рис. 2.11 Рис. 2.11 3. Дополнительный код получается образованием обратного кода с последующим прибавлением единицы к его младшему разряду. Пример. Представление числа –1 в дополнительном коде показано на рис. 2.12
Рис. 2.12 Представление числа –127 в дополнительном коде показано на рис. 2.13
Рис. 2.13 Обычно отрицательные десятичные числа при вводе в машину автоматически преобразуются в обратный или дополнительный двоичный код и в таком виде хранятся и участвуют в операциях. При выводе таких чисел из машины происходит обратное преобразование в отрицательные десятичные числа. Использование различных способов изображения отрицательных чисел в ЦВМ обуславливает целый ряд особенностей выполнения операции алгебраического сложения двоичных чисел. При сложении обратных кодов чисел Х1 и Х2 имеют место четыре основных и два особых случая. 1. Х1>0 и X2>0. При суммировании складываются все разряды, включая разряд знака. Пример Десятичная запись Двоичные коды
(5) + (9) (14) 2. Х1>0, X2<0 и |X2|>X1 Пример Десятичная запись Двоичные коды
+
При переводе обратного кода (обр) в прямой (пр) получим: 1 1111000обр=1 0000111пр= -710
3. Х1>0, X2<0 и |X2|<X1 Пример Десятичная запись Двоичные коды
+
Полученный непосредственно сразу неверный результат (число 6) исправляется путем переноса единицы из знакового разряда в младший разряд суммы. При этом получается правильный результат – число 710 4. Х1<0 и X2<0 Пример. Десятичная запись Двоичные коды
+
-10
Полученный непосредственно сразу неверный результат (обратный код числа –1110) исправляется путем переноса единицы из знакового разряда в младший разряд суммы. При выполнении операции может появиться число, старшие разряды которого не помещаются в отведенной для него области памяти – возникает переполнение разрядной сетки формата числа. Рассмотрим два возможных случая переполнения. 1. Х1>0 , X2>0 и S=X1+X2 Пример Десятичная запись Двоичные коды
+ 97
Здесь имеет место переполнение разрядной сетки: семи разрядов цифровой части недостаточно для размещения восьмиразрядной суммы (16210=101000102), поэтому старший разряд суммы оказывается в знаковом разряде и знак суммы оказывается несовпадающим со знаком слагаемых, что является признаком переполнения разрядной сетки. 2 Х1<0, X2<0 и S=|X1|+|X2| Пример Десятичная запись Двоичные коды
+
-158
Здесь также знак суммы не совпадает со знаками слагаемых, что является признаком переполнения разрядной сетки. При сложении дополнительных кодов чисел Х1 и Х2 имеют место те же четыре основных и два особых случая. 1. Х1>0 и X2>0. Аналогично случаю 1 для обратных кодов. 2. Х1>0, X2<0 и |X2|>X1. Пример. Десятичная запись Двоичные коды
-
При переводе дополнительного (доп) кода в прямой (пр) получим:
3. Х1>0, X2<0 и |X2|<Х1 Пример Десятичная запись Двоичные коды
-
Единица переноса из знакового разряда отбрасывается.
4. Х1<0, X2<0 Пример
-3 +
Случаи переполнения разрядной сетки аналогичны случаям переполнения для обратных кодов. Сравнение использования обратного и дополнительного кодов показывает, что преобразование отрицательного числа в обратный код занимает меньше времени, однако время выполнения сложения в дополнительных кодах меньше, чем в обратных, так как в этом случае отсутствует необходимость переноса единицы из знакового разряда в младший разряд результата. Основы алгебры логики. Алгебра логики – наука, которая занимается логическими функциями, описанием работы и синтезом с их помощью схем различных устройств ЦВМ. Алгебра логики имеет дело с высказываниями. Высказывания могут быть истинными или ложными. Если высказывание истинно, то значение истинности равно 1, если ложно -0. Высказывания могут быть простые и сложные, которые образуются из простых с помощью элементарных логических операций. Простые высказывания обычно называются также логическими переменными, сложные высказывания - логическими функциями. Основные элементарные логические операции: 1) Логическое отрицание. Обозначается чертой над логической переменной. Например Каждая логическая операция характеризуется таблицей истинности, которая показывает значение функции при всех значениях переменных. В данном случае таблица истинности содержит одну переменную, т.е.
0 1 1 0 Изоб
Рис. 2.14. Изображение основных логических элементов. а) элемент «НЕ»; б) элемент «ИЛИ»; в) элемент «И» 2) Логическое сложение (дизъюнкция). Обозначается значком V. Например Х1VХ2 читается как “Х1 или Х2”.Результаты логического сложения истинен (1) коли хотя бы одна из переменных (Х1 или X2) истинна (1) Таблица истинности
Изображение логического элемента “ИЛИ” на структурной схеме показано на рис.2.14 б.
3) Логическое умножение (конъюнкция). Обозначается значком ^. Например Х1^Х2 читается “Х1 и Х2”. Результат логического умножения истинен (1), только тогда, когда обе переменных истинны (1) Таблица истинности
Изображение логического элемента “И” на структурной схеме показано на рис.2.14в:
Основные законы алгебры логики: 1. Переместительный
2. Сочетательный
3. Распределительный
4. Отрицания
Справедливость любого закона может быть показана с помощью таблицы истинности. Покажем справедливость последнего закона
Из таблицы видно, что при всех сочетаниях значений логических переменных Х1 и Х2 значения логических функций

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
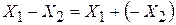
 -10
-10 -7
-7 0
0
 -3
-3 1
1
 -3
-3 -7
-7

 2n-1, где n – количество разрядов формата числа (для однобайтового формата n=8, 2n-1=27=128)
2n-1, где n – количество разрядов формата числа (для однобайтового формата n=8, 2n-1=27=128) 162
162 0
0
 -63
-63 -95
-95
 10
10 -7
-7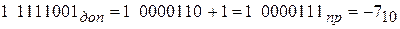
 0
0
 3
3 7
7 1
1
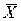 читается “не Х”.
читается “не Х”. Х
Х  ражение логического элемента “НЕ” на структурной схеме показано на рис. 2.14а.
ражение логического элемента “НЕ” на структурной схеме показано на рис. 2.14а.