|
|
Перевод чисел из одной системы счисления в другую.Перевод чисел из q-ичной системы счисления в десятичную при ручном счете для небольших чисел может быть осуществлен по формуле (2.5). Например,
В общем виде задачу перевода числа из одной системы счисления в другую можно представить как задачу определения коэффициентов нового ряда, изображающего число в новой системе счисления. Все действия должны выполняться по правилам исходной системы. После нахождения максимальной степени нового основания, проверяют «вхождение» в заданное число всех степеней нового основания, меньших максимального. Пример. Перевести десятичное число А=96 в троичную систему счисления.
9610=101203 Рассмотренный в этом примере прием может быть использован только при ручном переводе. Для реализации машинного алгоритма перевода число разделяют на целую и дробную части и каждую часть переводят отдельно. Перевод целых чисел осуществляется делением на основание новой системы. При этом целое число в новой системе счисления образуется начиная с младшего разряда из остатков, получаемых в результате последовательного деления целого числа на основание новой системы счисления. Процесс деления продолжается до тех пор, пока частное не станет равным нулю или меньшим основания. Рассмотрим перевод целых чисел на примере перевода из десятичной системы в двоичную. Пусть дано целое десятичное число А10. Перевести его в двоичную систему счисления – значит представить в виде
Задача заключается в нахождении коэффициентов a0, a1, a2… которые могут принимать значение 0 или1. Разделив целое число А10 на 2, получим новое целое число Разделив новое число А1 на 2 получим новое целое число
Пример 1.Перевести десятичное число А=18 в двоичную систему счисления. Разделив целое число 18 на 2, получим новое целое число А1=9 и остаток а0; разделив целое число А1 на 2 получим новое целое число А2= 4 и второй остаток а2 и т.д. Сказанное можно записать в виде. А1=9 a0=0
А3=2 a2=0 1810=100102 А4=1 a3=0 А5=0 a4=1 Перевод можно выполнить и в столбик
1810=100102
Пример 2. Перевести десятичное число А=37 в двоичную систему счисления.
3710=1001012
Пример 3. Перевести десятичное число А=249 в восьмеричную систему счисления.
24910=3718 Пример 4. Перевести двоичное число А2=1101001 в десятичную систему счисления. Основание 10 изображается в двоичной системе счисления эквивалентом 1010=10102
11010012=10510.
а0=0101=510, а1=0000=010; а2=0001=110 Перевод правильных дробей осуществляется умножением на основание новой системы исчисления. При этом дробное число в новой системы счисления образуется начиная со старшего разряда из целых частей, получаемых в результате последовательного умножения дробной части числа на основание новой системы счисления. Процесс умножения продолжается до тех пор, пока дробная часть не будет равна нулю (число переводится точно) или пока не получим требуемое число разрядов нового числа (число переводится приближенно). Рассмотрим перевод правильных дробей на примере перевода из из десятичной системы в двоичную. Пусть дано дробное десятичное число В10. Перевести его в двоичную систему счисления – значит представить в виде:
Задача заключается в нахождении коэффициентов b1, b2, b3 и т.д. Умножив число B на 2 получим
Умножив дробную часть В1 на 2 получим
Пример 1. Перевести десятичное число B=0,45 в двоичную систему счисления.
2В1=1,80 В2=0,80 b2=1 0,4510=0,01112 2В2=1,60 В3=0,60 b3=1 2В3=1,20 В4=0,20 b4=1
Перевод можно выполнить и в столбик.
0,4510=0,01112
Пример 2. Перевести десятичное число В=0,45 в восьмеричную систему счисления
0,4510=0,3468
Пример 3. Перевести двоичное число В=0 1101 в десятичную систему счисления (1010=10102)
0,11012=0,812510 В случае если исходное число состоит из целой и дробной частей каждая часть переводится отдельно, а затем они суммируются. Пример 1. Перевести число 35,510 в двоичную систему счисления Перевод целой части Перевод дробной части
0,510=0,12 3510=1000112
В итоге 35,510=100011,12
Пример 2. Перевести число 74,510 в восьмеричную систему счисления
7410=1128 0,510=0,48 В итоге 74,510=112,48 Перевод чисел из восьмеричной системы счисления в двоичную и обратно основан на использовании соотношения 23=8. Поэтому перевод восьмеричного числа в двоичную систему счисления осуществляется путем замены каждой цифры восьмеричного числа ее двоичным эквивалентом - 3-х разрядным двоичным числом (триадой). Пример. Перевести восьмеричное число А8=341,058 в двоичную систему счисления 341,058
341,058=011 100 001,000 1012 011 100 001, 000 101 Для перевода двоичного числа в восьмеричную систему счисления число нужно разбить на триады влево и вправо от запятой и каждую триаду заменить ее восьмеричным эквивалентом. Пример. Перевести двоичное число 1101101,1101 в восьмеричную систему счисления 001 101 101, 110 1002 1 5 5 6 4 1101101,11012=155,648 Перевод шестнадцатеричного числа в двоичную систему счисления основан на соотношении 24=16 и осуществляется путем представления каждой цифры числа в виде четырех разрядного двоичного числа (тетрады). Пример. Перевести шестнадцатеричное число 5A7B,6E в двоичную систему счисления
5A7B,6E16=0101 1010 0111 1011,0110 11102 0101 1010 0111 1011 0110 1110
Для перевода двоичного числа в шестнадцатеричную систему счисления число нужно разбить на тетрады влево и вправо от запятой и каждую тетраду заменить ее шестнадцатеричным эквивалентом. Пример. Перевести двоичное число 1110101111,01101112 в шестнадцатеричную систему счисления
3 А F 6 Е 1110101111,011011102=3AF,6E16
Следует отметить, что помимо систем счисления в ЦВМ используются различные коды, например “2-10” код. Для представления десятичного числа в “2-10” коде каждую цифру числа представляют в виде тетрады. Пример. Представить число 563,9110 в “2-10” коде 5 6 3 9 1 10 0101 0110 0011 1001 0001 563,9110=0101 0110 0011,1001 00012-10
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
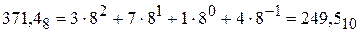
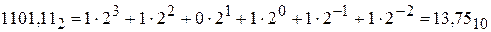
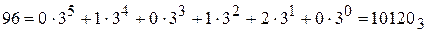
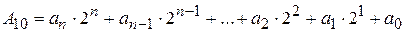
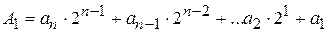и остаток a0, являющийся младшим разрядом двоичного числа.
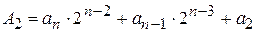и остаток a1, являющийся следующим разрядом двоичного числа и т.д. до тех пор, пока целая часть не станет равной 0.
А2=4 a1=1
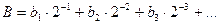
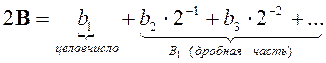
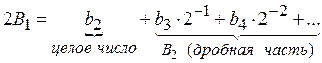и т.д. до тех пор, пока дробная часть не станет равной 0 или не получим требуемое число двоичных разрядов.
2В=0,90 В1=0,90 b1=0
0,
1010
0,
2
5A7B,6E16
