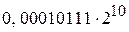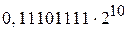|
|
Формы представления числовой информацииСуществует две формы представления чисел: естественная или с фиксированной запятой (точкой) и нормальная или с плавающей запятой. Представление чисел с фиксированной запятой характеризуется тем, что положение запятой фиксируется перед каким-либо разрядом, например, перед старшим разрядом. В этом случае для машинного изображения
т.е. числа имеют вид правильных дробей. В этом смысле число Х будет представлено в виде Диапазон представимых чисел составляет от
Рис. 2.8. Представление чисел в форме с фиксированной запятой.
Задача выбора масштабного коэффициента К усложняется в связи с необходимостью сохранять соответствие разрядов всех чисел, с которыми оперирует компьютер. Пусть разрядная сетка ЦВМ содержит 12 двоичных разрядов (рис. 2.8а). Надо определить масштабный коэффициент для чисел Для того, чтобы выполнить условие (2.11) необходимо число, большее по абсолютному значению, записать в виде Из данного примера видно, что представление чисел в форме с фиксированной запятой может привести к погрешности представления. Так, для числа Х2 абсолютная погрешность представления оценивается величиной части числа, не уместившейся в разрядную сетку, т.е. величиной Представления чисел в форме с плавающей запятой характеризуется тем, что число представляется в нормальной форме
где m – мантисса числа х; р - порядок числа х. Такое представление числа неоднозначно. Например, десятичное число 485,00 можно записать различными способами: Для определенности обычно вводят некоторые ограничения. Наиболее распространено и удобно для распространения в ЭВМ ограничение вида
где q – основание системы счисления. Из этого следует, что мантисса должна быть правильной дробью, первая цифра которой отлична от нуля: Форма представления чисел, для которой справедливо условие (2.13) называется нормализованной. Поскольку в этом случае абсолютное значение мантиссы находится в пределах
Рассмотрим пример записи чисел в форме с плавающей запятой. Пусть требуется записать в разрядную сетку ЦВМ двоичные числа
Поскольку для изображения порядка выделено пять цифровых разрядов и один разряд для знака, машинные изображения порядков:
машинные изображения их мантисс соответственно:
Представление чисел Х1 и Х2 в разрядной сетке показано на рис. 2.9 б,в соответственно. В современных ЦВМ используется оба способа представления чисел, каждый из которых имеет свои достоинства и недостатки. Представление чисел в форме с фиксированной запятой хотя и доставляет некоторые трудности при программировании, связанные с введением масштабов, позволяет упростить схемы АЛУ и повысить его быстродействие, так как арифметические операции над числами выполняются без предварительных действий (выравнивания порядков). Пример. Сложить два двоичных положительных числа 0,0000011 и 0,0000111
(310)
(710) 1010 Пример. Сложить два двоичных нормализованных положительных числа
Результат получился нормализованным. В противном случае его бы следовало нормализовать в соответствии с условием (2.13).

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 числа Х должно выполняться условие
числа Х должно выполняться условие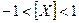 (2.11)
(2.11) , где К масштабный коэффициент, величина которого удовлетворяет условию (2.11). Так как числа бывают положительные и отрицательные, то формат (разрядная сетка) разбивается на знаковую часть и поле числа (рис. 2.8а). В знаковую часть записывается информация о знаке. Обычно знак положительного числа «+» изображается символом 0, а знак отрицательного числа «-» изображается символом 1.
, где К масштабный коэффициент, величина которого удовлетворяет условию (2.11). Так как числа бывают положительные и отрицательные, то формат (разрядная сетка) разбивается на знаковую часть и поле числа (рис. 2.8а). В знаковую часть записывается информация о знаке. Обычно знак положительного числа «+» изображается символом 0, а знак отрицательного числа «-» изображается символом 1.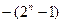 до
до  , где n - количество разрядов без знаковой части
, где n - количество разрядов без знаковой части
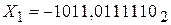 и
и 
 . Отсюда
. Отсюда  (рис.2.8б), что соответствует величине масштабного коэффициента
(рис.2.8б), что соответствует величине масштабного коэффициента  . Число Х2 должно войти в разрядную сетку с сохранением соответствия разрядов, т.е.
. Число Х2 должно войти в разрядную сетку с сохранением соответствия разрядов, т.е.  . Следовательно,
. Следовательно,  или
или 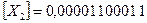 (рис. 2.8 в).
(рис. 2.8 в).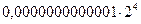 . В некоторых случаях очень малые числа представляются в машине изображением, называемым машинным нулем. Если в результате какой-либо операции появится число, по абсолютному значению большее единицы, то возникает переполнение разрядной сетки, что нарушает нормальное функционирование ЦВМ.
. В некоторых случаях очень малые числа представляются в машине изображением, называемым машинным нулем. Если в результате какой-либо операции появится число, по абсолютному значению большее единицы, то возникает переполнение разрядной сетки, что нарушает нормальное функционирование ЦВМ.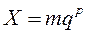 , (2.12)
, (2.12)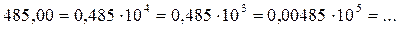
 , (2.13)
, (2.13) Мантиссу и порядок q –ичного числа принято записывать в системе с основанием q, а само основание в десятичной системе.
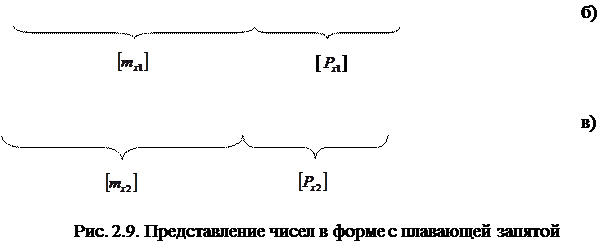
Мантиссу и порядок q –ичного числа принято записывать в системе с основанием q, а само основание в десятичной системе. где n – количество разрядов изображения мантиссы без знака. Поскольку положение разрядов числа в разрядной сетке машины не постоянно, такую форму представления чисел называют также формой представления с плавающей запятой. Формат машинного изображения числа с плавающей запятой должен содержать знаковые части и поля для числа (мантиссы) и порядка (рис. 2.9а). Кодирование знаков остается таким же, как и при представлении чисел с фиксированной запятой.
где n – количество разрядов изображения мантиссы без знака. Поскольку положение разрядов числа в разрядной сетке машины не постоянно, такую форму представления чисел называют также формой представления с плавающей запятой. Формат машинного изображения числа с плавающей запятой должен содержать знаковые части и поля для числа (мантиссы) и порядка (рис. 2.9а). Кодирование знаков остается таким же, как и при представлении чисел с фиксированной запятой.
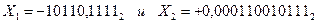 . Эти числа следует представить в нормализованном виде, т.е. при выполнении условия (2.13):
. Эти числа следует представить в нормализованном виде, т.е. при выполнении условия (2.13):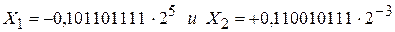
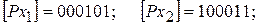
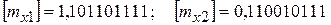
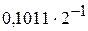 и
и 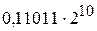 . Разность порядков слагаемых здесь равна трем, поэтому перед сложением мантисса первого числа сдвигается на три разряда вправо
. Разность порядков слагаемых здесь равна трем, поэтому перед сложением мантисса первого числа сдвигается на три разряда вправо