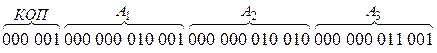|
|
Глава 2. Основы аналоговых и цифровых вычисленийПринципы построения вычислительных машин Средства вычислительной техники можно классифицировать по различным признакам, но главенствующим из них является способ представления информации (сигналов): в непрерывном (аналоговом) или дискретном (цифровом) виде (см. рис.2.1а, г). Вычислительные машины, в которых используется представление информации в непрерывной форме, называются вычислительными машинами непрерывного действия или аналоговыми вычислительными машинами (АВМ), так как имеет место аналогия в представлении информации в машине и в окружающей нас жизни – обычно информация представляется в непрерывной форме. Вычислительные машины, в которых используется представление информации в дискретной форме называются вычислительными машинами дискретного действия или цифровыми вычислительными машинами (ЦВМ), так как значение функций в них представляется в виде чисел – в цифровой форме (обычно в двоичной системе счисления). Поясним принцип действия АВМ. Они состоят из решающих блоков, выполняющих различные математические операции над переменными: умножение на постоянный коэффициент, суммирование, интегрирование, нелинейное преобразование и др. Физическая природа переменной, а, следовательно, и решающих блоков может быть различной (механические, гидравлические, пневматические, электронные) и соответственно различной физической природы могут быть АВМ. Наибольшее распространение получили электронные АВМ, в которых машинной переменной является напряжение постоянного тока. Основным решающим элементом таких АВМ является операционный усилитель, построенный на базе усилителя постоянного тока с очень большим коэффициентом усиления –Ку (усилитель имеет нечетное число каскадов усиления) и внешних элементах Z1 и Z0 , в общем виде являющихся комплексными сопротивлениями. (рис.2.1 а). Главная особенность этой схемы состоит в том, что так как Ку очень большая величина, потенциал точки g можно считать близким к нулю (точка g потенциально заземлена) и связь выходного и входного напряжений определяется только внешними элементами Z1 и Z0 . В зависимости от вида сопротивлений Z1 и Z0 схема выполняет различные математические операции. Так, при Z1 и Z0 чисто активных сопротивлениях, т.е. Z1=R1, Z0=R0 схема принимает вид, показанный на рис.2.1.б. В этом случае i1=i0 или
Рис. 2.1. Операционный усилитель. а) в общем виде; б) схема умножения на постоянный коэффициент и ее условное обозначение; в) схема суммирования и ее условное обозначение; г) схема интегрирования и ее условное обозначение; д) схема интегрирования с одновременным суммированием и ее условное обозначение
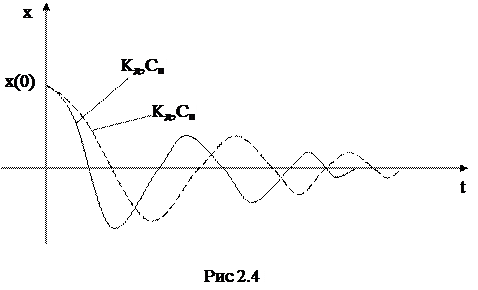
Для собственно усилителя Uвых=-КуUg (2.2) Так как Ку величина очень большая (обычно Ку>107) можно считать
Тогда из (2.1) следует:
т.е. схема выполняет операцию умножения входного напряжения на постоянный коэффициент На рис. 2.1 в, г, д показаны соответственно схемы операционного усилителя, выполняющие операции суммирования, интегрирования и суммирования с одновременным интегрированием и их условные обозначения. АВМ обычно используются для исследования (моделирования) технических систем, описываемых обыкновенными дифференциальными уравнениями. Рассмотрим пример. Пусть требуется исследовать механическую систему (рис.2.2), состоящую из платформы массой m, демпфера (коэффициент демпфирования
В соответствии со вторым законом Ньютона
где F – силы, действующие на тело.
Обозначим
Для решения этого дифференциального уравнения на АВМ необходимо обеспечить на входе интегрирующего блока 1 правую часть уравнения (2.3) (рис.2.3 а). Тогда на выходе блока 1 будет получена переменная –
Схема моделирования позволяет выяснить влияние различных параметров системы на ее свойства (переходной процесс). Например, по изменению напряжения на выходе блока 2 можно судить о характере движения системы при различных значениях
АВМ имеют ограниченную точность решения, которая зависит от типа и числа решающих элементов, занятых в схеме моделирования. Поэтому АВМ используются для моделирования технических объектов, имеющих определенные допуска на изготовление, где высокая точность решения не обязательна. Цифровые вычислительные машины принципиально отличаются от аналоговых. В отличие от АВМ в ЦВМ машинной переменной является не модель самой физической величины, а модель ее дискретного числового эквивалента, характеризуемого количеством разрядов. В связи с этим ЦВМ, в отличие от АВМ, могут выполнять преобразования с любой заданной точностью, определяемой числом разрядов и шагом дискретизации. В отличие от аналоговых цифровые преобразования выполняются последовательно, т.е. операция за операцией. Отсюда следует, что быстродействие ЦВМ, хотя и очень высокое, принципиально ограничено. В то же время выполнение операций последовательно позволяет их автоматизировать, и для этого заранее составляется программа последовательности вычислений и ввода/вывода. Наконец, в отличие от АВМ, ЦВМ являются универсальными, так как используют численные методы, позволяющие свести решение разнообразных задач к выполнению простейших арифметических и логических действий, которые ЦВМ и могут выполнять с высокой скоростью и большой точностью. Так, например, задача вычисления определенного интеграла, т.е. площади подынтегральной функции (рис.2.5) на ЦВМ может быть сведена, в простейшем случае - методом прямоугольников, к стандартной задаче вычисления суммы чисел, т.е.
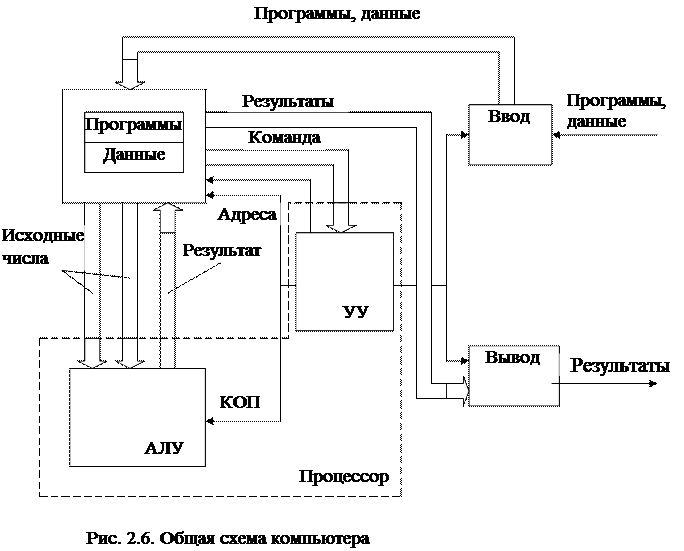
Заканчивая сравнение аналоговых и цифровых вычислительных машин следует указать на существование класса комбинированных (гибридных) вычислительных машин, состоящих из АВМ, ЦВМ и преобразователей аналого-цифрового (АЦП) и цифро-аналогового (ЦАП). При этом аналоговая часть используется обычно для моделирования объекта, а цифровая – для решения уравнений движения объекта, т.е. там где требуется высокая точность решения. Основу современных цифровых вычислительных машин (компьютеров) образует аппаратура (Hardware), построенная в основном с использованием электронных и электромеханических устройств. Принцип действия компьютеров состоит в выполнении программ (Software) – четко определенных последовательностей команд, т.е. последовательностей арифметических и логических операций. Разнообразие современных компьютеров очень велико, но их структуры основаны на общих логических принципах, позволяющих выделить в любом компьютере следующие основные устройства: запоминающее устройство (ЗУ), арифметико-логическое устройство (АЛУ), устройство управления (УУ), устройство ввода и устройство вывода результатов. Эти устройства соединены каналами связи (рис. 2.6). Двойными стрелками показано движение информации, простыми стрелками – передача управляющих сигналов. Программа и исходные данные, подлежащие обработке, с помощью устройства ввода (например, клавиатуры) поступают в ЗУ, которое состоит из ячеек. Каждая ячейка имеет номер, называемый ее адресом в ЗУ. В каждую ячейку может быть записано или из нее прочитано одно число (данное) или одна команда. Число или команда называется машинным словом. При записи слова в ячейку предыдущее слово автоматически стирается. При прочитывании слова прочитанное по прежнему сохраняется в ячейке с помощью специальной системы регенерации.
Емкость памяти можно выразить количеством содержащихся в ней ячеек. Длина ячейки памяти измеряется количеством битов (двоичных разрядов), т.е. единица измерения памяти совпадает с единицей измерения информации. Биты объединяются в группы по 8 бит, которые называются байтами. Все байты пронумерованы, номер байта называется его адресом. Для каждого компьютера характерна определенная длина слова – два, четыре или восемь байт. Ячейка памяти может вмещать информацию и другой длины – полуслово, двойное слово. На рис. 2.7 представлено разбитие памяти на слова для четырехбайтовых компьютеров.
Рис. 2.7
Широко используются и более крупные производные единицы объема памяти: 1 Килобайт = 210 байт = 1024 байт
Арифметико-логическое устройство является основным преобразователем цифровой информации и предназначено для выполнения арифметических и логических операций, заданных программой. Устройство управления обеспечивает взаимодействие всех устройств в процессе выполнения задачи, т.е. автоматический ввод программы, автоматическое выполнение команд программы и автоматическую выдачу результатов. АЛУ и УУ конструктивно образуют процессор. В составе процессора имеются регистры – специальные электронные схемы памяти, обеспечивающие кратковременное хранение числа или команды. Основным элементом регистра является триггер – электронная схема, способная хранить один двоичный разряд. Регистр представляет собой совокупность триггеров, связанных между собой общей системой управления. Современный процессор выполняется в виде микропроцессора, представляющего собой интегральную схему. В основу построения большинства компьютеров положены общие принципы, сформулированные в 1945г. американским ученым Джоном фон Нейманом. Рассмотрим два основных принципа. 1. Принцип программного управления. Программа состоит из набора команд, которые выполняются в определенной последовательности автоматически. Выбор команды программы из памяти осуществляется с помощью специально регистра – счетчика команд, содержимое которого увеличивается на единицу после выполнения очередной команды. При этом организуется выборка цепочки команд из последовательно расположенных ячеек памяти, (естественный порядок выполнения команд). В случае необходимости перехода не к следующей, а к другой команде используются команды передачи управления, которые заносят в счетчик команд адрес ячейки памяти, содержащей следующую команду. Выборка команд из памяти прекращается после достижения и выполнения команды «стоп». 2. Принцип однородности памяти. Команды и данные хранятся в одном и том же запоминающем устройстве. Команды и данные по виду не различаются, т.к. представляют собой набор нулей и единиц, но заранее известно, что хранится в этой ячейке памяти – число, текст или команда. Над командами можно выполнять различные действия, как и над данными. Поэтому команда в процессе выполнения программы может видоизменяться. Рассмотрим более подробно понятие команды. Как уже было сказано, команда – это описание элементарной арифметической или логической операции, которую должен выполнить компьютер. В общем случае команда содержит информацию о коде выполняемой операции, указаний по определению адресов данных (операндов) и указаний по размещению получаемого результата. В зависимости от количества адресов команды бывают одно-, двух-, трехадресные. Возможны и переменно-адресные команды. Рассмотрим несколько возможных вариантов команды сложения. При этом вместо цифровых кодов и адресов будем использовать условные коды и условные адреса. Одноадресная команда Сл
Двухадресная команда Сл
Трехадресная команда Сл
Совокупность команд, выполняемых данным компьютером, составляет систему команд этого компьютера. Рассмотрим принцип действия фон-неймановской ЦВМ. Для этого предварительно составим программу для решения простой вычислительной задачи, имеющей чисто методический смысл. Пусть требуется вычислить арифметическое выражение S=(5+8)*7-2 Сначала программа составляется в условных адресах. Пусть
К+1, К+2,… - адреса ячеек для хранения команд программы Тогда программа для условной трехадресной ЦВМ будет иметь вид:
Составим программу в конкретных адресах Пусть Пусть Пусть Пусть Пусть операции Сл., Умн., Выч., Печ., Стоп имеют коды 01, 05, 02, 21, 33 соответственно. Тогда программа в конкретных адресах будет иметь вид
ЦВМ работают в двоичной системе счисления, поэтому адреса ячеек, числа и команды в ЦВМ представлены в двоичной системе счисления, т.е. состоят из определенного количества разрядов (нулей и единиц). Например, команда 0051, т.е. команда, хранящаяся в ячейке 0051 (в двоичной системе 000 000 101 001) имеет вид:
Программу в конкретных адресах в двоичной системе счисления называют также программой в машинных кодах или программой на машинном языке. С появлением в 60-х годах алгоритмических языков высокого уровня пользователи ЦВМ освободились от необходимости составлять программу на машинном языке. Эту операцию выполняет специальная программа – транслятор, также находящаяся в ЗУ и обеспечивающая перевод программы с языка высокого уровня на машинный язык и автоматическое распределение памяти.
Как уже было сказано, команды в ЦВМ выполняются последовательно. Каждая команда также выполняется по шагам, или по тактам. Рассмотрим взаимодействие устройств ЦВМ (см. рис. 2.6) на примере выполнения по тактам команды 0051. Предварительно в счетчике команд, находящемся в устройстве управления, устанавливается число 0051. Команда выполняется по тактам: 1. Содержимое ячейки 0051, т.е. хранящаяся там команда 000 001 000 000 010 001 000 000 010 010 000 000 011 001 поступает на регистр команд устройства управления. Команда разделяется на кодовую и адресную части. Код операции (000 001) поступает в АЛУ для подготовки его к выполнению данной операции (сложение) 2. УУ обращается по первому адресу (А1), т.е. к ячейке 0021 и хранящееся в ней число (5) поступает на первый регистр АЛУ. 3. УУ обращается по второму адресу (А2), т.е. к ячейке 0022 и хранящиеся в ней число (8) поступает на второй регистр АЛУ 4. АЛУ выполняет операцию сложения чисел 5 и 8. Результат находится на сумматоре АЛУ. 5. УУ направляет результат по третьему адресу (А3), т.е. в ячейку 0031. В ячейке 0031 будет находиться число 13. На этом выполнение команды заканчивается. В счетчике команд добавляется 1 и ЦВМ автоматически переходит к выполнению следующей команды – 0052, т.е. к опросу ячейки 0052, извлечению хранящейся в ней команды, которая выполняется по тактам и т.д. до тех пор пока ЦВМ не дойдет до команды “Стоп”

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 (2.1)
(2.1)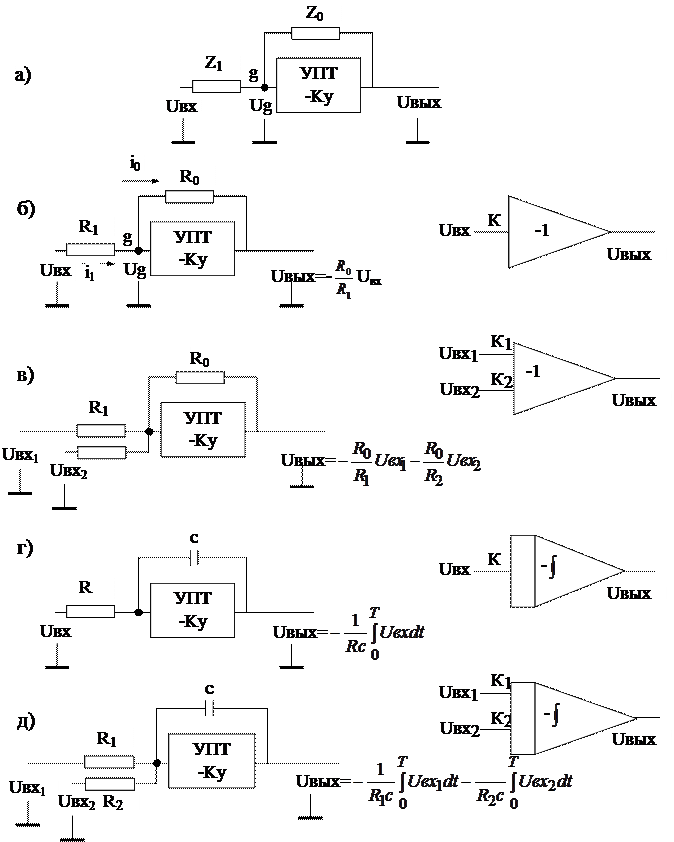
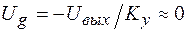
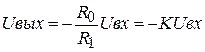
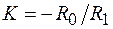
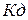 ) и пружин (жесткость пружин
) и пружин (жесткость пружин  ).
).
 ,
,
 и
и  . Тогда
. Тогда или
или (2.3)
(2.3) . Если последовательно с блоком 1 подключить блоки 2 и 3 (рис. 2.3 б) и соединить выходы блоков 2 и 3 с соответствующими входами блока 1, получим схему, показанную на рис.2.3 в. Эта схема является электронной моделью исследуемой системы (рис.2.2), описываемой уравнением (2.3) и называется схемой моделирования. Для того, чтобы схема моделирования приняла конкретный вид вводят масштабные коэффициенты по всем переменным, ставя в соответствие максимально допустимое значение напряжения максимальному значению соответствующей переменной, и определяют конкретные значения величин R и C для всех блоков.
. Если последовательно с блоком 1 подключить блоки 2 и 3 (рис. 2.3 б) и соединить выходы блоков 2 и 3 с соответствующими входами блока 1, получим схему, показанную на рис.2.3 в. Эта схема является электронной моделью исследуемой системы (рис.2.2), описываемой уравнением (2.3) и называется схемой моделирования. Для того, чтобы схема моделирования приняла конкретный вид вводят масштабные коэффициенты по всем переменным, ставя в соответствие максимально допустимое значение напряжения максимальному значению соответствующей переменной, и определяют конкретные значения величин R и C для всех блоков.


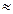 1000 байт; 1 Мегабайт
1000 байт; 1 Мегабайт  : содержимое ячейки
: содержимое ячейки  сложить с содержимым сумматора, а результат сохранить в сумматоре
сложить с содержимым сумматора, а результат сохранить в сумматоре : содержимое ячеек
: содержимое ячеек  : содержимое ячейки
: содержимое ячейки 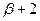 , - адреса ячеек для хранения промежуточных результатов;
, - адреса ячеек для хранения промежуточных результатов; ,
,  … - адреса ячеек для хранения окончательных результатов;
… - адреса ячеек для хранения окончательных результатов;
 -----
-----
-----
-----
 , тогда
, тогда 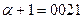 ,
,  ,
,  ,
, 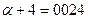
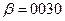 , тогда
, тогда 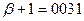

 , тогда
, тогда 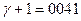
 , тогда
, тогда  ,
, 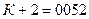 ,…….,
,…….,  .
.