
|
|
Передача информации. Меры информации.Представим, что на вход информационного устройства после преобразований поступает входной сигнал, имеющий вид дискретного множества х1, х2, …, хn. Задача информационного устройства состоит в том, чтобы перевести вектор сигнала на входе Х (х1, х2, …, хn) в соответствующий ему вектор сигнала на выходе Y (y1,y2,…,yn) с высокой достоверностью (без ошибок или с допустимыми ошибками). В процессе передачи сигнал может быть подвергнут различным преобразованиям, меняющим его физические характеристики. Однако информация, содержащаяся в сигнале, должна быть инвариантна ко всем преобразованиям. Прежде всего нужно определить числовую, количественную меру информации, содержащейся во входном сигнале. Для этого надо знать объем множества возможных состояний сигнала. Принято называть множество возможных символов сигнала алфавитом, отдельный символ – буквой алфавита, комбинацию символов – словом (состоянием, последовательностью символов). Простейший алфавит имеет два символа: 0 и 1; «+» и « – »; «ДА» и «НЕТ». Если каждое слово состоит из одной буквы, то число возможных слов (состояний, сочетаний) N=21=2 (0 и 1). Если каждое слово состоит из двух букв, то число возможных слов N=22=4. Если алфавит имеет три слова, например, a, b, c, то при выборах по два символа число возможных слов N=32=9 (табл.1.1). При выборах по 3 символа N=33=27 и т.д.
Таблица 1.1 В общем случае, при числе символов S в алфавите и числе букв n в слове, число возможных слов N=Sn. (1.53) Число N называется комбинаторной мерой информации. Однако величина N неудобна для практической оценки информационной емкости, так как при заданном S количество информации растет экспоненциально с увеличином n - числом букв в слове, причем вклад каждого последующего значения n нарастает. Для того, чтобы мера информации имела практическую ценность необходимо, чтобы количество информации I было пропорционально числу n, т.е. должно обеспечиваться соотношение: I=Kn, (1.54) где K– постоянная, не зависящая от S. Допустим, что имеются две системы символов S1 и S2; им соответствует K1 и K2 такие, что если
то и I=K1n1=K2n2. (1.56) Из (1.55) и (1.56) следует, что
Это соотношение тождественно, если K=logs, т.е. K1=logS1, (1.58) K2=logS2. Подставив (1.58) в (1.54) и используя (1.53) получим: I=nlogS=logSn=logN, (1.59) т.е. в качестве меры информации I может быть принят логарифм числа возможных слов (состояний) N. Рассмотрим насколько функция I отражает количественную оценку информации. Для этого должны выполняться 3 условия: 1. Априори известно, что количество информации системы, имеющей одно состояние, равно 0. Действительно, в соответствии с (1.59) I=I(1)=log1=0, т.е. условие выполняется. 2. Допустим, что физическая система состоит из двух независимых систем и является их объединением. Обозначим: N; I – общее число состояний и количество информации всей системы соответственно; N1; I1 – число состояний и количество информации первой системы; N2; I2 – число состояний и количество информации второй системы. Очевидно, что N=N1N2 (одному состоянию первой системы соответствует N2 состояний второй системы и т.д.) Общее количество информации I=I(N)=I(N1N2).Естественно считать, что суммарная информация должна быть равна сумме информации первой и второй системе, т.е. обладать свойством аддитивности, т.е. I(N1N2)=I(N1)+I(N2) Действительно, в соответствии с (1.59) I=I(N)=logN=log(N1N2)=logN1+logN2, т.е. условие выполняется. 3. Естественно потребовать, чтобы зависимость количества информации от числа состояний была монотонной, т.е. I(N2) > I(N1) при N2>N1. Действительно в соответствии с (1.59) I(N2)=logN2; I(N1)=logN1, I(N2)>I(N1) при N2>N1. Таким образом оценка меры информации I в соответствии с (1.59) удовлетворяет всем трем условиям. Величина I называется хартлиевской (аддитивной) мерой информации по имени ученого Р.В.Л. Хартли, который, рассматривал процесс получения информации, как выбор одного сообщения (символа) из конечного наперед заданного множества N равновероятных и независимых сообщений, а количество информации I , содержащееся в выбранном сообщении, определял как двоичный логарифм N, т.е. I=log2N (1.60) Отметим, что величина I безразмерна, т.е. не связана с физическими параметрами сигнала, а только с числом его состояний. Так как единица информации (I=1) соответствует числу состояний N=2, то можно считать, что единица информации – это количество информации, которое можно записать (закодировать) с помощью двух символов: 0 и 1. Поскольку каждый разряд в двоичной системе счисления может принимать значения 0 или 1, т.е. содержит одну единицу информации, было принято название единицы информации – один бит (англ. binary dijit – двоичная цифра; здесь игра слов; «bit» - частица чего-либо, в данном случае информации). Отметим, что количество информации I в случае десятичного логарифма в (1.60) измеряется в дитах, в случае натурального логарифма – в нитах. Следовательно, один бит информации соответствует одному элементарному событию, которое может произойти или не произойти. Такая мера количества информации дает возможность оперировать мерой как числом. Количество информации в соответствии с (1.60) эквивалентно количеству битов - двоичных символов (нулей и единиц). Отсюда можно сделать вывод: чтобы измерить количество любой информации нужно представить ее в виде последовательностей нулей и единиц наиболее рациональным способом (дающим минимум знаков). Длина (количество знаков) последовательности нулей и единиц может служить мерой информации. Рассмотрим несколько примеров на определение количества информации. Пример 1. Имеется 8 букв: a, b, c, d, e… Требуется определить количество содержащейся информации. Для этого каждую букву нужно представить в виде последовательности из нулей и единиц. Для представления (кодирования) всех букв нужно иметь восемь последовательностей, причем в каждой будет по три цифры (нулей и единиц). Например a=000; b=001; c=010; d=011 и т.д. Следовательно, количество информации равно трем битам. Этот ответ и дает формула (1.60): I=log2 8=3 бита. Аналогичный подход может быть использован для оценки количества информации при выборе одного сообщения из N равноправных (равновероятных) сообщений. Пример 2. Имеется колода карт, содержащая 32 различные карты. Требуется определить количество информации при выборе одной карты. Априори естественно предположить, что вероятность выбора некоторой определенной карты одинакова для всех карт колоды. Поэтому для выбора одной карты из колоды имеем оценку количества информации: I=log232=5 бит. Полученная оценка имеет интересную итерпретацию. Количество информации I характеризует число двоичных («да»-«нет» -ных) вопросов, необходимых для выбора (угадывания) одного сообщения из ряда N равновероятных сообщений. Следовательно, возвращаясь к данному примеру, для выбора одной карты надо задать 5 двоичных вопросов. Например, для выбора дамы пик такими вопросами будут: 1. Карта красной масти? Ответ «нет» 0. 2. Трефы? Ответ «нет» 0. 3. Одна из четырех старших? Ответ «да» 1. 4. Одна из двух старших? Ответ «нет» 0. 5. Дама? Ответ «да» 1. Этот выбор можно описать последовательностью из пяти двоичных символов 00101 (0-нет, 1-да). Процесс замены ответов на 1 и 0 называется кодированием, полученная последовательность – кодовым символом. Длина кодового слова соответствует мере информации. В случае если количество выборов не равно степени двойки получается нецелое число вопросов. Например, если взять колоду из 36 карт, то может оказаться, что в ряде случаев для выбора определенной карты может понадобиться 5 вопросов, как и в предыдущем случае, а в ряде случаев – 6 вопросов. Усреднение по случаям и дает получаемую по формуле 1.60, не целую величину меры информации. Пример 3. На лекции 16 студентов. Лектор запомнил одну фамилию. Сколько надо задать вопросов, чтобы узнать кого он запомнил? Количество информации I=log2 16=4 бита. Для решения задачи нужно всем студентам присвоить номера от 0 до 15, а затем порядковый номер каждого представить в виде четырехзначной последовательности из нулей и единиц (в двоичной системе). Например, 0-0000; 1-0001; 2-0010; 3-0011 и т.д. Например, для N6-0110. Тогда 4 вопроса, которые нужно задать, будут: верно ли, что в двоичной записи номеров фамилии первая, вторая, третья и четвертая цифры равны 1. Ответ: «нет», «да», «да», «нет», т.е. кодовое слово 0110. Пример 4. В городе 5 миллионов жителей. Загадали одного. Сколько надо задать вопросов, чтобы отгадать? Количество информации I=log2 5000000=23 бита (222=4194304; 223=8388608). Ответ: надо задать 23 вопроса. Следовательно формулу Хартли (1.60) можно интерпретировать и таким образом: если в заданном множестве G, содержащем N элементов, выделили элемент X, о котором известно, что он принадлежит множеству G, то чтобы найти Х, надо получить количество информации, равное I=log2 N. Мера информации по Хартли (1.60) хотя и позволяет измерять количество информации, содержащейся в сигнале, и используется на практике, но имеет ограниченное применение. Дело в том, что хартлиевская мера оценки информации зависит только от числа N возможных состояний источника информации и не учитывает различной вероятности появления отдельных символов, составляющих эти состояния. Предполагается, что эти вероятности одинаковы, т.е. каждый символ несет одинаковое количество информации. В общем случае, при посылке N последовательных независимых сигналов, вероятности появления отдельных символов в них могут быть различны, что не может не сказаться на количестве поступающей информации. Так, очевидно, что если один из символов появляется часто и вероятность его появления близка к единице, то такой символ несет мало информации. Столь же мало информативны символы вероятность появления которых близка к нулю. В связи с этим в теории информации принят более общий – вероятностный (энтропийный) подход к оценке информации. Сущность этого подхода заключается в том, что мера информации, поступающей от символа, зависит от вероятности его появления в сигнале. Количество информации, поступающей от каждого символа в случае, когда они равновероятны может быть получено из формулы (1.60) и выражается в битах
где Предположим, что в определенные фиксированные моменты времени t, количество которых равно М, приемник воспринимает сигналы x(t), состоящие из N дискретных символов (значений), причем в каждый момент времени может появиться один из символов, заранее неизвестно какой. Тогда в результате приема М сигналов можно определить частоту (вероятность) появления каждого из N символов, как отношение числа появления этого символа к общему числу М. В результате может быть получена таблица (табл. 1.2), в которой указываются дискретные значения сигнала и вероятности их появления, причем эти значения образуют полную группу событий, т.е.
Табл. 1.2 Предположим, что в результате приема M сигналов ί-тый символ повторяется Кi раз и каждый раз вносит информацию, количество которой оценивается как Ii . Тогда средняя информации, доставляемая в результате одного опыта
но количество информации от одного символа Ii связано с вероятностью его появления Рi в соответствии с (1.61)
Тогда или
Отношения
или Другими словами, если Ii – частное количество информации от одного символа (1.63), то среднее количество информации Iср равно математическому ожиданию частных количеств информации, т.е.
При равновероятных и независимых символах все P=1/N и формула (1.65) преобразуется в формулу Хартли (1.60). Формулу (1.65) называют формулой Шеннона (по имени математика К. Шеннона). Величину H называют энтропией, которая является мерой неопределенности. Поясним смысл формулы Шеннона. Для этого рассмотрим серию опытов, в результате каждого из которых имеет место одно из несовместимых событий Х1, Х2, Х3 …ХN, образующих полную группу событий, для которой справедливо
Для примера пусть число событий N=8, каждое событие содержит 3 символа и имеет вероятность Рi (табл. 1.3)
Табл. 1.3 Предположим, что вероятности всех возможных результатов выражаются числами
Из таблицы 1.3 видно, что если вероятность какого-либо события равна При проведении опытов количество двоичных знаков в числе, соответствующем номеру опыта, будет случайной величиной с возможными средними значениями Естественно, за меру неопределенности H принять среднее арифметическое значение числа двоичных знаков необходимых, чтобы полностью определить общий результат, т.е. определить величину Среднее арифметическое значение случайной величины
или
В нашем примере
Это и есть математическое ожидание числа двоичных знаков на одно сообщение. Если предположить, что вероятности всех восьми сообщений равны друг другу, т.е. каждое сообщение имеет одинаковое количество информации, то Понятие информации, как было показано выше, тесно связано с понятием неопределенности. Мера неопределенности есть непрерывная функция вероятностей состояний источника информации. Чем больше вероятность, не получая информацию, правильно угадать состояние системы, тем меньше неопределенность источника, и наоборот, чем меньше априорная вероятность события, тем большее количество информации оно несет, тем больше его неопределенность. Например, имеются 2 источника (Табл. 1.4а и 1.4б)
а) б) Табл. 1.4 Ясно, что у 2-ого источника неопределенность меньше: он на 99% находится в состоянии Х1; 1-ый источник с вероятностью 0,5 (или на 50%) находится в состоянии Х1. Таким образом сообщение несет полезную информацию тогда, когда имеется энтропия – неопределенность состояний источника сообщений. Если опыт имеет один исход, то получатель знает исход опыта заранее и не получает никакой информации (неопределенность отсутствует). Если опыт имеет два исхода – имеет место определенная информация и неопределенность. Чем меньше априори вероятность события, тем большее количество информации оно имеет. Рассмотрим основные свойства энтропии. 1. Энтропия равна нулю, т.е. 2. Энтропия максимальна, т.е. т.е. соответствует оценке меры информации по Хартли (1.60), определяющей максимальное количество информации. Следствия: – для равновероятных состояний энтропия есть монотонно возрастающая функция числа состояний.
Например, имеется 2 источника – табл. 1.5 а и б.
а) б) Табл. 1.5 Для первого источника априори известно 50% исходов, а для второго – 10%, т.е. для первого источника возможности выбора (неопределенность) меньше, чем для второго. - энтропия есть вещественная ограниченная и неотрицательная функция, т.к. - всякое изменение вероятностей P1, P2,….PN в сторону их выравнивания увеличивает энтропию - Энтропия есть математическое ожидание логарифма вероятности, т.е. Если энтропия источника раскрывается по этапам, то полная энтропия будет суммой энтропий, полученных на каждом этапе.
Сначала делаем выбор между двумя возможными вероятностями, равными 1/2 и 1/2, а затем для второй возможности выбора делаем выбор между возможностями с вероятностями 2/3 и 1/3 от 1/2. Окончательно имеем те же вероятности, что и прежде. В этом случае требуется, чтобы
Коэффициент 1/2 во втором члене суммы связан с тем, что выбор на втором этапе происходит только в половине общего числа случаев. Рассмотрим вопрос о единицах измерения энтропии. В силу безразмерности вероятностей энтропия является безразмерной величиной. Однако для практических целей необходимо ввести единицу ее измерения. За единицу измерения энтропии может быть принята энтропия любого объекта, для которого
В общем случае в (1.66) неизвестных три: число возможных состояний N, вероятность Pi, и основание логарифма. Два из этих неизвестных можно задать, а третье получить из (1.66). В простейшем случае N=2, а P1=P2=1/2, тогда
Таким образом единицей измерения энтропии служит энтропия системы с двумя равновероятными состояниями, вычисленная с помощью логарифма, с основанием 2. Это двоичная единица энтропии - «бит». В случае десятичной системы счисления (основание а=10) единицей измерения энтропии служит энтропия системы с десятью равновероятными состояниями, вычисленная с помощью десятичных логарифмов. Это десятичная единица энтропии – «дит». Очевидно, что если в системах с единичной энтропией принять закон равных вероятностей
На практике имеет место применение натурального логарифма с основанием е – в этом случае единица энтропии имеет название «нит». Так как
1дит=3,32бита, 1нит=1,51бита. Рассмотрим ряд примеров по определению количества информации и энтропии.
Пример 1. Система имеет 64 элемента, один из которых неисправен. Вероятности того, что неисправен любой элемент, одинаковы. Определить количество информации I в сообщении о результате проверки одного элемента. Каждый элемент есть источник с двумя состояниями: х1-исправен, х2-неисправен. Вероятности состояний показаны в таблице 1.6
Табл. 1.6 Количество частной информации I в сообщении, что проверяемый элемент исправен, равно
Количество частной информации I в сообщении, что проверяемый элемент неисправен, равно
Количество информации I(x) в сообщении о проверке одного элемента
Пример 2. Вероятность выхода из строя некоторого прибора при включении равна Р0. После k-го включения прибор проверяют. Найти k из условия максимума информации, получаемой при проверке. Вероятность исправной работы после первого включения равна 1-р, после k-го включения Рu=(1-p)k. Вероятность неисправного состояния после k-го включения Максимум информации соответствует равновероятным состояниям, т.е.
Пример 3. Какова Hmax системы, состояние которой заключается в расположении одной фигуры на одном из 64 полей шахматной доски? Энтропия равна Hmax, когда события равновероятны. В случае равновероятных состояний в соответствии с (1.67) Если фигура чернопольная, то Пример 4. Какова Hmax сообщения состоящего из пяти букв при общем количестве 32 буквы в алфавите. Количество возможных состояний в соответствии с (1.53) По существу энтропия (неопределенность) есть не что иное, как недостаток информации, или ее отрицательная величина. Иначе говоря, в общем случае количество информации представляет собой убыль энтропии в следствии проведения какого-либо опыта. В случае, когда неопределенность снимается полностью количество информации I равно энтропии, т.е. I=H, причем неопределенность будет наибольшей, когда вероятности событий одинаковы. Это соответствует максимально возможному количеству информации, оцениваемому мерой Хартли: В общем случае имеет место частичная информация, которая представляет собой разность между начальной Н1 и конечной Н2 энтропией, т.е. I=H1-H2=ΔH. Энтропия источника тесно связана с понятием избыточности информации. Абсолютная избыточность источника информации
Относительная избыточность
Как видно из (1.68) чем больше энтропия источника Hmax, тем выше его избыточность и наоборот. Пример. Пусть полная шкала измерений содержит 1000 единиц (квантов), допускаемая погрешность Всю шкалу достаточно разделить на 50 квантов и В случае если для измерения используется непрерывная шкала, т.е. Избыточность увеличивает надежность передачи информации, так как появляется возможность исправления ошибок, возникающих в канале связи вследствие действия помех, однако избыточность одновременно уменьшает скорость передачи информации. При передаче через канал связи без помех последовательности дискретных сообщений длительностью Т, скорость передачи информации I по каналу связи.
Предельное значение скорости передачи информации называется пропускной способностью канала связи без помех Для наиболее эффективного использования канала связи необходимо, чтобы скорость передачи информации была как можно ближе к пропускной способности канала связи. Если скорость поступления информации на вход канала связи превышает пропускную способность канала, то по каналу будет передана не вся информация. Основное условие согласования источника информации и канала связи Согласование осуществляется путем соответствующего кодирования сообщений. Если ко входу канала подключен источник сообщений с энтропией, равной пропускной способности канала связи, то считается, что источник согласован с каналом. Если энтропия источника меньше пропускной способности канала, что может быть в случае неравновероятности состояний источника, то источник не согласован с каналом, т.е. канал используется не полностью. Согласование в статистическом смысле достигается с помощью статистического кодирования. Оно позволяет повысить энтропию передаваемых сообщений до величины, которая получается, если символы новой последовательности равновероятны. При этом число символов в последовательности будет сокращено. В результате источник информации согласуется с каналом связи. При передачи информации через канал с помехами сообщения искажаются и на приемной стороне нет уверенности в том, что принято именно то сообщение, которое передавалось. Следовательно, сообщение недостоверно, вероятность правильности его после приема не равна единице. В этом случае количество получаемой информации уменьшается на величину неопределенности, вносимой помехами, т.е. вычисляется как разность энтропии сообщения до и после приема: Таким образом, скорость передачи по каналу связи с помехами
Пропускной способностью канала с шумами называется максимальная скорость передачи информации при условии, что канал связи без помех согласован с источником информации:
Если энтропия источника информации не превышает пропускной способности канала (Н
где Fm – полоса частот канала (Гц); Wc – средняя мощность сигнала; Wш – средняя мощность шумов (равномерный спектр) с нормальным законом распределения амплитуд в полосе частот канала связи. Следовательно, можно передавать информацию по каналу с помехами без ошибок, если скорость передачи информации меньше пропускной способности канала, определяемой формулой (1.71). Для скорости Подобно тому, как Хартлиевская мера информации используется для выбора одного состояния системы из ряда N равновероятных состояний, энтропия может быть использована для определения минимального количества двоичных вопросов необходимых для выбора (отгадывания) одного состояния системы из ряда N возможных неравновероятных состояний. Энтропия Предположим, что имеется источник с N возможными состояниями и энтропией Н(x). Требуется определить одно из состояний системы. Для этого используется принцип последовательного образования равновероятных групп. Вначале все состояния источника разделяют на две группы Х1 и Х2 (табл. 1.7), где Р - вероятность первой группы состояний. Когда состояния равновероятные, ответ дает максимальную информацию, равную 1 биту.
Табл. 1.7
Полученный ответ не снимает полностью неопределенность, он только указывает группу, в которой находится состояние источника. Далее выбранную группу снова разделяют на две равновероятные группы. Ответ («Да» или «Нет») в свою очередь дает информацию равную одному биту. Таким образом, после двух ответов получено два бита информации. Для полного устранения неопределенности надо получит количество информации, равное энтропии источника Н [бит]. Следовательно, энтропия определяет минимальное количество вопросов, с помощью которых можно полностью определить состояние системы. Вопросы должны быть поставлены так, чтобы ответы были равновероятны. Если на поставленный вопрос возможны m ответов, то состояния системы перед очередным вопросом надо делить на m равновероятных групп. В этом случае основание логарифма при определении Н будет равно m. Пример 1. Имеется 9 шаров, один тяжелее. Есть чашечные весы Определить минимальное число взвешиваний. Одно взвешивание (один вопрос) дает три равновероятных ответа: «слева», «справа», «не на весах».
Следовательно, минимальное число взвешиваний равно 2. (Сначала делим шары на три группы по три шара, определяем нужную тройку, затем из этой тройки по одному шару на весы).
Пример 2. Имеется система трех последовательно соединенных элементов (рис. 1.14)
рис. 1.14
Известно, что неисправен один из элементов. Вероятности неисправности каждого элемента показаны на рисунке 1.14. Определить энтропию системы В соответствии с (1.65)
Следовательно, минимальное число проверок равно 1,5. Разбиваем элементы на 2 группы с равными вероятностями Р=1/2. В первую группу входят первый элемент, во вторую – второй и третий элементы. При первой проверке проверяем первый элемент: если он неисправен (ответ «да»), то проверка закончена, если он исправен (ответ «нет»), то проверка продолжается во второй группе. При второй проверке проверяется второй элемент: если он неисправен (ответ «да»), то проверка закончена, если он исправен (ответ «нет») – то неисправен третий элемент. Среднее количество проверок (с Р=1/2 неисправен первый элемент – одна проверка; с Р=1/2 – неисправны второй и третий элементы – две проверки):
Вопросы для самопроверки 1. Какие проблемы рассматривает «теория информации»? 2. В чем отличие сигналов детерминированных от случайных? 3. В чем отличие стационарных случайных сигналов от нестационарных? 4. В чем заключается эргодическая теорема? 5. Что представляют собой дискретизация во времени и квантование по уровню непрерывного сигнала? 6. В чем заключается теорема В.А. Котельникова? 7. В чем заключается процесс модуляции и демодуляции сигнала? 8. Поясните смысл оценки меры информации по Р. Хартли. 9. Поясните смысл оценки меры информации по К. Шеннону. 10. Дайте определение понятию «энтропия». Назовите основные свойства энтропии. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , (1.55)
, (1.55) или
или  . (1.57)
. (1.57) (1.61)
(1.61) - вероятность появления каждого из символов, образующих полную группу событий
- вероятность появления каждого из символов, образующих полную группу событий  .
. .
. , (1.62)
, (1.62) (1.63)
(1.63)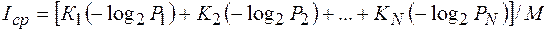
 (1.64)
(1.64) представляют собой частоты повторения символов, а следовательно могут быть заменены их вероятностями, т.е.
представляют собой частоты повторения символов, а следовательно могут быть заменены их вероятностями, т.е.  . Поэтому средняя информация в битах
. Поэтому средняя информация в битах (1.64)
(1.64) (1.65)
(1.65)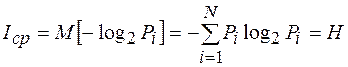
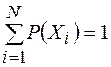
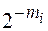
 , где
, где  – целые положительные числа. причем
– целые положительные числа. причем 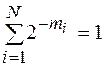
 -значным двоичным числом.
-значным двоичным числом. .
. .
.
 (1.66)
(1.66)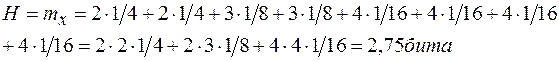
 , что соответствует мере информации по Хартли
, что соответствует мере информации по Хартли  бита. Таким образом может иметь место экономия в числе передаваемых символов при одной и той же информации.
бита. Таким образом может иметь место экономия в числе передаваемых символов при одной и той же информации. , в том крайнем случае, когда одно из чисел
, в том крайнем случае, когда одно из чисел  равно 1, следовательно, остальные равны нулю. Это тот случай когда об опыте или величине все известно заранее, он имеет один исход, и результат не дает новую информацию.
равно 1, следовательно, остальные равны нулю. Это тот случай когда об опыте или величине все известно заранее, он имеет один исход, и результат не дает новую информацию. , когда все состояния системы равновероятны, т.е.
, когда все состояния системы равновероятны, т.е.  . При этом
. При этом  , (1.67)
, (1.67)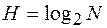
 ,
, 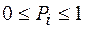
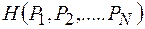
 . Это выражение имеет такой же вид, как и выражение для энтропии, используемое в термодинамике и статистической механике.
. Это выражение имеет такой же вид, как и выражение для энтропии, используемое в термодинамике и статистической механике. Пример. Пусть имеется три события с вероятностями Р1=1/2, Р2=1/3, Р3=1/6. (рис 1.13). Энтропия будет
Пример. Пусть имеется три события с вероятностями Р1=1/2, Р2=1/3, Р3=1/6. (рис 1.13). Энтропия будет  .
.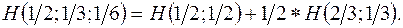
 (1.66)
(1.66)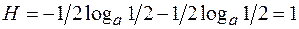
 Отсюда а=2.
Отсюда а=2. , то
, то и поскольку
и поскольку  , то всегда N=a
, то всегда N=a , то соотношения между единицами:
, то соотношения между единицами: бита
бита бита
бита





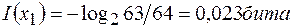
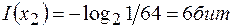
 .
. .
. или
или , откуда
, откуда и
и  .
. .
. .
. .
.  , когда состояния равновероятны. По формуле (1.67)
, когда состояния равновероятны. По формуле (1.67) 
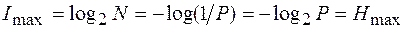
 представляет собой разность между максимально возможным количеством информации и энтропией
представляет собой разность между максимально возможным количеством информации и энтропией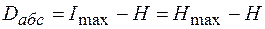 (1.68)
(1.68) (1.69)
(1.69) 1% от полной шкалы, т.е.
1% от полной шкалы, т.е.  .
. , то при любых начальных значениях допустимой погрешности избыточность максимальна, т.е.
, то при любых начальных значениях допустимой погрешности избыточность максимальна, т.е.  .
. (бит/с).
(бит/с). . Так как количество информации в сообщениях максимально при равной вероятности состояний, то
. Так как количество информации в сообщениях максимально при равной вероятности состояний, то  . Количественно пропускная способность канала связи выражается максимальным количеством двоичных единиц информации, которое данный канал связи может передать за одну секунду.
. Количественно пропускная способность канала связи выражается максимальным количеством двоичных единиц информации, которое данный канал связи может передать за одну секунду.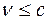 .
. , где Н(i) – энтропия источника сообщений;
, где Н(i) – энтропия источника сообщений;  - энтропия сообщения на приемной стороне.
- энтропия сообщения на приемной стороне. (1.70)
(1.70) .
. с), то существует код, обеспечивающий передачу информации через канал с помехами со сколь угодно малой частотой ошибок или сколь угодно малой недостоверностью. Пропускная способность канала связи при ограниченной средней мощности аналогового сигнала
с), то существует код, обеспечивающий передачу информации через канал с помехами со сколь угодно малой частотой ошибок или сколь угодно малой недостоверностью. Пропускная способность канала связи при ограниченной средней мощности аналогового сигнала , (1.71)
, (1.71) >c при любой системе кодирования частота ошибок принимает конечное значение, причем оно растет с увеличением значения
>c при любой системе кодирования частота ошибок принимает конечное значение, причем оно растет с увеличением значения  только при двух равновероятных значениях Р(0)=Р(1)=1/2, (в других случаях Н меньше одного бита и Н=0 при Р(0)=0, Р(1)=1 или Р(1)=1, Р2=0). Следовательно, при ответе на двоичный вопрос количество информации зависит от того, какова вероятность получить утвердительный ответ, причем Р=1/2 соответствует максимуму информации. Отсюда следует практический вывод: если случайная величина ξ принимает значения с разными вероятностями, то при выборе (отгадывании) вопрос надо задавать так, чтобы вероятность ответа («да» или «нет») как можно меньше отличалась от 0,5; при этом ответ будет содержать наибольшее количество информации.
только при двух равновероятных значениях Р(0)=Р(1)=1/2, (в других случаях Н меньше одного бита и Н=0 при Р(0)=0, Р(1)=1 или Р(1)=1, Р2=0). Следовательно, при ответе на двоичный вопрос количество информации зависит от того, какова вероятность получить утвердительный ответ, причем Р=1/2 соответствует максимуму информации. Отсюда следует практический вывод: если случайная величина ξ принимает значения с разными вероятностями, то при выборе (отгадывании) вопрос надо задавать так, чтобы вероятность ответа («да» или «нет») как можно меньше отличалась от 0,5; при этом ответ будет содержать наибольшее количество информации.



 ,
, Р1=1/2 Р2=1/4 Р3=1/4
Р1=1/2 Р2=1/4 Р3=1/4
 проверки.
проверки.