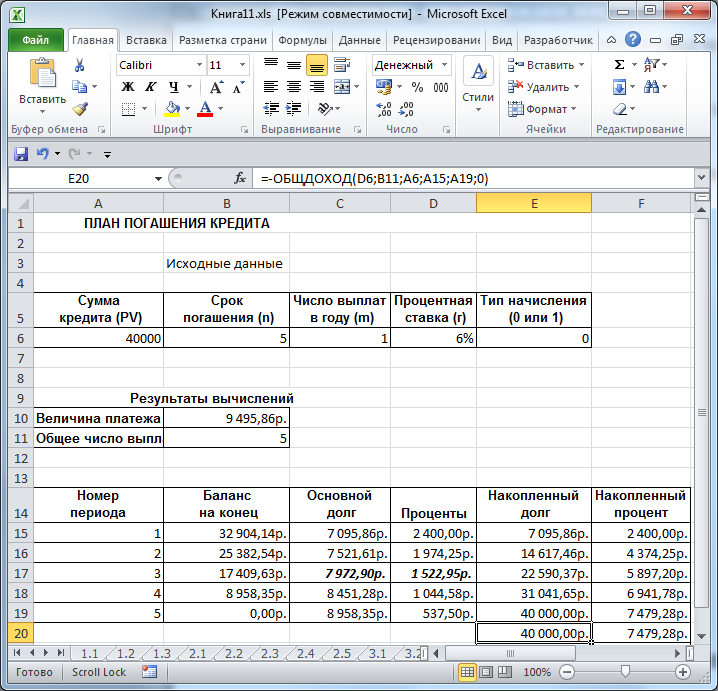
ПЛТ — расчет постоянных периодических выплат

Функция вычисляет величину выплаты за один период на основе фиксированных периодических выплат и постоянной процентной ставки. Выплаты, рассчитанные функцией ПЛТ, включают основные платежи и платежи по процентам.

Синтаксис

ПЛТ(ставка;кпер;пс;бс;тип)

Пример 21Предположим, что необходимо накопить 4000 руб. за 3 года, откладывая постоянную сумму в конце каждого месяца. Какой должна быть эта сумма, если норма процента по вкладу составляет 12% годовых?

Величина ежемесячных выплат составит:

ПЛТ(12%/12;12*3;;-4000)= 92.86 руб.

ОСПЛТ — расчет основных платежей по займу

Функция вычисляет величину основного платежа (выплаты задолженности) по займу, который погашается равными платежами в конце или начале каждого расчетного периода, на указанный период.

Синтаксис

ОСПЛТ(ставка;период;кпер;пс;бс;тип)

Пример 22Банком выдан кредит в 7000 руб. на 3 года под 17% годовых, начисляемых один раз в конце каждого периода.

Определите размер ежегодных основных выплат по займу.

Основная часть платежа на каждый из трех периодов составит соответственно:

ОСПЛТ(17%;1;3;-70000)=19780.16 руб.

ОСПЛТ(17%;2;3;-70000)=23142.78 руб.

ОСПЛТ(17%;3;3;-70000)=27077.06 руб.

Комплексный пример

Банк выдал долгосрочный кредит в сумме 40 000$ на 5 лет под 6% годовых. Погашение кредита должно производиться равными ежегодными выплатами в конце каждого года, включающими погашение основного долга и процентные платежи. Начисление процентов производится 1 раз в год. Составить план погашения займа.

Решение:

Периодический платеж по данной операции составит

ПЛТ(6%;5;-40000)=9495,86$.

Рис.1. План погашения кредита

Процентная часть платежа на первый период составит:

ПРПЛТ(6%;1;5;-40000)=2400,00$.

Основная часть платежа, направленная на погашение долга за первый период, составит:

ОСПЛТ(6%;1;5;-40000)=7095,86$.

Как видно выполняется тождество:

ПЛПРОЦ()+ОСНПЛАТ()=ППЛАТ()=9495,86$.

Будущее значение суммы, которую банк получит в результате проведения операции:

ПЛТ(6%;5;-40000)*5=47479,28$.

Лабораторная работа

ФИНАНСОВЫЕ ФУНКЦИИ EXCEL

Решить без использования встроенных функций

Задача 1.

В банке открыт срочный депозит на сумму 50 тыс. руб. по 12% на 3 года. Рассчитать наращенную сумму если проценты:

а) простые

б) сложные.

Задача 2.

В банке открыт срочный депозит на сумму 100 тыс. руб. по 15% на 3 года. Рассчитать наращенную сумму, если проценты начисляются ежеквартально.

Задача 3.

Банк предлагает два варианта депозита

1) под 120% с начислением процентов в конце года

2) под 100% с начислением процентов в конце каждого квартала.

Определить более выгодный вариант размещения депозитов на один год.

Задача 4.

Банк принимает депозиты по ставке 50% с начислением процентов ежеквартально. Определить эффективную ставку.

Задача 5.

Процентная ставка 50% с начислением процентов в конце срока. Рассчитать эквивалентную ставку с начислением процентов раз в 6 месяцев.

Решить, используя встроенные функции

ЗАДАЧА 1. Сумма вклада, помещенного в банк на 5 лет под 5% годовых, составляет 10000 ден. ед.

1.1. Определите будущую величину вклада, если начисле­ние процентов осуществляется:

а) раз в году;

б) раз в полгода;

в) раз в квартал;

г) раз в месяц.

1.2. В предположении, что целью вкладчика является нако­пление суммы 15000 ден.ед. определите, какова должна быть сумма начального вклада при тех же условиях (срок вклада - 5 лет , годовой процент - 5%). Использовать аппарат Подбор параметра или функцию ПС

ЗАДАЧА 2. Фирма «X» предполагает взять кредит в 100000 ден.ед. на 5 лет под 12% годовых. Проценты начисляются еже­квартально и подлежат выплате вместе с основной суммой долга по истечении срока кредита. Определите сумму выплаты на мо­мент погашения кредита.

Допустим, что фирма «X» имеет альтернативную возмож­ность получения кредита в 100000 ден. ед. На 5 лет под 11% го­довых, выплачиваемых ежемесячно. Какой вариант получения кредита выгоднее?

ЗАДАЧА 3. По вкладу в 10000 ден. ед., помещенному в банк под 5% годовых, начисляемых ежегодно, была выплачена сумма 12762,82. Определите срок проведения операции (количество пе­риодов начисления).

ЗАДАЧА 4. Фирма определила возможную для себя ежеме­сячную выплату по кредиту 720 тыс. руб. Зная размер ежемесяч­ных выплат, размер кредита 45000 тыс. руб., процентную ставку 12%, определите количество платежей (месяцев) для расчета по кредиту.

ЗАДАЧА 5. Фирма хотела взять валютный кредит на 5 лет под 10% годовых, выплачивая проценты один раз в конце года. За год фирма имеет возможность выплачивать не более 1000$. Оп­ределите сумму кредита, который может получить фирма.

Дополнительные задачи

Задача 1.

Капитал величиной 4 000 денежных единиц (д. е.) вложен в банк на 90 дней под 8,7% годовых. Какова будет его конечная величина.

Задача 2.

На сколько лет нужно вложить капитал под 9% годовых, чтобы процентный платеж был равен его двойной сумме.

Задача 3.

Пусть в банк вложено 20 000 д. е. под 10% годовых. Найти конечную сумму капитала, если расчетный период составляет:

а) 3 месяца;

б) 1 месяц.

Задача 4.

Номинальная годовая ставка — 12%. Найти уравнивающую про­центную ставку при начислении сложных процентов каждые 3 месяца.

Задача 5.

По одному из вкладов в банке в течение 20 лет накоплено 200000 д. е. Найти сумму, положенную на счет первоначально, если годовая процентная ставка составляет 9%.

Задача 6.

Каждые три месяца в банк вкладывается по 500 д. е. Какова будет совокупная сумма этих вкладов в конце 10-го года при процен­тной ставке 8% и годовой капитализации.

Задача 7.

Насколько увеличатся годовые вклады по 2 000 д. е. в течение 4 лет при 8% годовых, если капитализация производится раз в три месяца и первый вклад вносится в конце первого года.

Задача 8.

Пусть первый вклад в банк составляет 2 000 д. е., а каждый последующий уменьшается на 100 д. е. по отношению к предыдуще­му. Найти величину вкладов в конце 10-го года, если они произво­дятся ежегодно, процентная ставка — 4% годовых, капитализация ежегодная.

Задача 9.

Найти текущую стоимость суммы 10 вкладов по 5 000 д. е. при 8% годовых, если капитализация осуществляется каждые полгода.

Самостоятельная работа студентов

Контрольная работа

Контрольная работа включает два теоретических вопроса и 7 задач.

Номер теоретических вопросов соответствует последней цифре номера зачетной книжки.

Вопрос №1

1. Методы финансовой математики. Основные понятия в финансовых методах расчета.

2. Необходимость учета фактора времени в финансовых расчетах

3. Проценты. Единицы измерения процентов. Практика начисления простых процентов при различной величине временной базы. Различие между простыми и сложными ставками процентов.

4. Дисконтирование. Виды дисконтирования. Сущность понятия «дисконт».

5. Номинальная и эффективная ставки процентов

6. Модель сложных процентов

7. Расчет срока ссуды и процентных ставок

8. Потоки платежей. Определение и характеристики

9. Кредиты. Способы погашения кредитов.

10. Наращение и выплата процентов в потребительском кредите.

Не нашли, что искали? Воспользуйтесь поиском по сайту: