
|
|
Формула сложных процентовСодержание
1.ЕДИНОВРЕМЕННЫЕ ПЛАТЕЖИ.. 4 1.1 ОСНОВНЫЕ ПОНЯТИЯ.. 4 1.2 ПРОСТЫЕ ПРОЦЕНТЫ.. 5 1.3 СЛОЖНЫЕ ПРОЦЕНТЫ.. 6 1.3.1 Формула сложных процентов. 6 1.3.2 Определение будущей суммы.. 7 1.3.3 Определение текущей стоимости. Дисконтирование. 8 1.3.4 Определение срока ссуды (вклада) 9 1.3.5 Определение размера процентной ставки. 9 1.3.6 Номинальная и эффективная ставки. 9 Типовые задачи. 10 2. ПОСТОЯННЫЕ РЕГУЛЯРНЫЕ ПОТОКИ ПЛАТЕЖЕЙ.. 12 2.1 ОСНОВНЫЕ ПОНЯТИЯ.. 12 2.2 БУДУЩАЯ СУММА ПРЕНУМЕРАНДО И ПОСТНУМЕРАНДО БЕЗ ПЕРВОНАЧАЛЬНОЙ СУММЫ.. 13 2.2.1 Рента пренумерандо. 13 2.2.2 Рента постнумерандо. 13 2.3 УРАВНЕНИЕ ЭКВИВАЛЕНТНОСТИ В ОБЩЕМ ВИДЕ. 15 2.3.1 Определение будущей суммы.. 15 2.3.2 Определение текущей суммы.. 15 2.3.3 Определение периодических выплат.. 16 2.3.4 Расчет срока ренты.. 16 2.3.5 Определение размера процентной ставки. 17 Типовые задачи. 17 2.4 РЕШЕНИЕ ФИНАНСОВЫХ ЗАДАЧ С ПОМОЩЬЮ ФИНАНСОВЫХ ФУНКЦИЙ Excel 19 2.4.1 Общие рекомендации. 19 2.4.2 Вычисление будущего значения. 19 2.4.3 Расчет текущей суммы.. 20 2.4.4 Расчет срока ренты.. 21 2.4.5 Определение размера процентной ставки. 22 2.4.6 Выбор банка кредитования и составление плана погашения кредита 22 Лабораторная работа. 26 Контрольная работа. 28 Список литературы.. 30 ЕДИНОВРЕМЕННЫЕ ПЛАТЕЖИ ОСНОВНЫЕ ПОНЯТИЯ В основе всех финансовых расчетов лежит принцип временной ценности денег. Деньги - это мера стоимости товаров и услуг. Покупательная способность денег падает по мере роста инфляции. Это означает, что денежные суммы, полученные сегодня (обозначим их PV-present value- настоящее, текущее значение), больше, ценнее тех же сумм, полученных в будущем. Для того чтобы деньги сохраняли или даже наращивали свою ценность, нужно обеспечить вложение денег, приносящее определенный доход. Принято обозначать доход буквой I (interest), на финансовом и бытовом жаргоне его называют процентом. Существует много способов вложения (инвестиции) денег. Можно открыть счет в сберегательном банке, но процент должен превышать темп инфляции. Можно одолжить деньги в виде кредита с целью получения в будущем, так называемой, наращенной суммы FV (future value - будущее значение). А можно инвестировать денежные средства в производство. Простейшей финансовой операцией является однократное предоставление или получение суммы PV с условием возврата через время t наращенной (будущей) суммы FV. Сумму, которую получает дебитор (например, мы с Вами или фирма), будем считать положительной, а ту, которую отдает кредитор (опять же мы с Вами или банк) - отрицательной.
Эффективность такой операции характеризуется темпом прироста денежных средств, отношением r (rate-отношение) дохода I к базовой величине PV, взятыми по абсолютной величине. Темп роста капитала r за время t выражают десятичной дробью или в процентах и называют процентной ставкой, нормой доходности или скоростью оборота денежныхсредств за это время. Поскольку PV и FV имеют противоположные знаки, то настоящее и будущее значения связаны соотношением (назовем его уравнением эквивалентности)
FV+ PV (1+r)=0, (2)
где r - процентная ставка за время t. Величину К, показывающую, во сколько раз будущая сумма возросла по абсолютному значению по отношению к текущей К= FV/ PV=(1+r), (3) называют коэффициентом наращения капитала. В расчетах, как правило, за r принимают годовую процентную ставку, ее называют номинальной ставкой. Существуют две схемы наращения капитала: · схема простых процентов; · схема сложных процентов.
ПРОСТЫЕ ПРОЦЕНТЫ
Схема простых процентов предполагает неизменность суммы, на которую происходит начисление процентов. Простые проценты используются в краткосрочных финансовых операциях (со сроком менее периода начисления процентов) или когда проценты периодически выплачиваются и не присоединяются к основному капиталу. Рассмотрим два вида вклада: постой и срочный. 1) По простому вкладу(деньги по такому вкладу можно снять в любой момент) за t дней будет начислено
FV+ PV (1+ где Т - число дней в году. Коэффициент наращения при этом К=(1+ В зависимости от определения Т и t применяют следующие методики. 1. Точные проценты. В России, США, Великобритании и во многих других странах принято считать Т =365 в обычном году и Т =366 - в високосном, а t -число дней между датой выдачи (получения) ссуды и датой ее погашения. Дата выдачи и дата погашения считаются за один день. 2. Банковский метод. В этом методе t определяется как точное число дней, а число дней в году принимается за 360. Метод дает преимущества банкам особенно при выдаче кредита на срок более 360 дней и широко используется коммерческими банками. 3. Обыкновенные проценты с приближенным числом дней. В некоторых странах, например во Франции, Бельгии, Швейцарии принимают Т =360, а t -приближенным, так как считается, что в месяце 30 дней.
Пример 1 Фирма взяла ссуду в банке на расширение производства в размере 1 млн. руб. под 18% годовых с 20.01 по 05.10 включительно. Какую сумму она должна вернуть в конце срока при начислении процентов один раз в год? Определите коэффициент наращения. Решение. Пусть год не високосный Т=365. Точное число дней между указанными датами 1. Из (4) по точному методу получим FV= -1 000 000(1+ Итак, в конце срока фирме придется отдать (FV отрицательно) на 127 233 руб. больше, чем она брала. Коэффициент наращения в этом случае К=(1+ 2. По банковскому методу FV= -1 000 000(1+ К=(1+ 3. По обыкновенному методу с приближенным числом дней FV= -1 000 000(1+ К=(1+
Как видно из примера, при банковском методе расчета банку удастся больше "поживиться" за счет фирмы. 2) По срочному вкладу (деньги кладутся в банк на определенный срок: полгода, год или другой) проценты начисляются через определенные периоды. Обозначим m =12 - при ежемесячном начислении процентов; m =4 - при ежеквартальном начислении; m =2 - при начислении раз в полугодие; m =1 - при начислении раз в год. В этом случае процентная ставка за один период составит величину
FV + PV (1+ Коэффициент наращения К=(1+ Пример 2 Пенсионер положил 3000 руб. на срочный пенсионный вклад на полгода под 14% годовых. Какая сумма у него накопится в конце срока, и какой процент он сможет снять? Каков коэффициент наращения? Решение. Поскольку пенсионер отдал свои деньги банку, то первоначальная сумма отрицательна; m =2, так как начисления - раз в полгода. FV = -(-3000)(1+0,14/2)=3210 руб. I= FV- PV=210 руб. К=1+0,14/2=1,07 По формулам (2)-(.5) можно решить обратную задачу: какую первоначальную сумму PV нужно дать в долг или положить в банк, чтобы по истечении срока получить сумму FV при заданной годовой процентной ставке r:
Пример 3 Через 180 дней после подписания договора фирма обязуется уплатить 310 тыс. руб. Кредит выдан под 16% годовых. Какова первоначальная сумма кредита? Решение. В конце срока фирма должна вернуть деньги, следовательно, будущая сумма - отрицательная величина, а первоначальная - положительная. Из (5)
СЛОЖНЫЕ ПРОЦЕНТЫ Формула сложных процентов Схема сложных процентов предполагает их капитализацию, таким образом, базовая сумма, с которой происходят начисления, постоянно растет. Сложные проценты применяются в среднесрочных и долгосрочных финансовых операциях, то есть срок операции составляет несколько периодов начисления процентов. Пусть Вы положили в банк срочный вклад в сумме PV на k лет под годовую процентную ставку r. Число периодов начисления процентов в году m .Тогда в соответствии с формулой (4) к концу первого периода, т.е. после первого начисления процентов, у Вас окажется сумма FV, определяемая соотношением FV + PV (1+ Если Вы не забрали причитающиеся Вам проценты, то к началу нового периода первоначальная сумма составит уже PV(1+r/m), а к концу второго периода на нее снова нарастут проценты и Ваша сумма вклада будет определяться из соотношения
и так далее. К концу года Ваш вклад будет равен
Сумма, накопленная Вами в банке через k лет при годовой ставке r и начислениях процентов m раз в году, составит:
Эквивалентное уравнение (6) называют формулой сложных процентов. Из уравнений (4) - (6) можно определить одну из величин: FV - будущую сумму; PV - текущую сумму; r - номинальную процентную ставку; t или k - срок сделки в днях или годах, выразив их через остальные известные величины.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 . (1)
. (1) r)=0 (4)
r)=0 (4) 0,18)= -1 127 233 руб.
0,18)= -1 127 233 руб. 0,18)=1,1273
0,18)=1,1273 0,18)= -1 129 000 руб.
0,18)= -1 129 000 руб. 0,18)=1,129
0,18)=1,129 0,18)= -1 127 500 руб.
0,18)= -1 127 500 руб. 0,18)=1,1275
0,18)=1,1275 , и уравнение эквивалентности запишется в виде:
, и уравнение эквивалентности запишется в виде: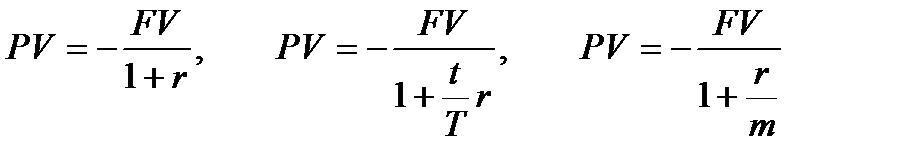 .
.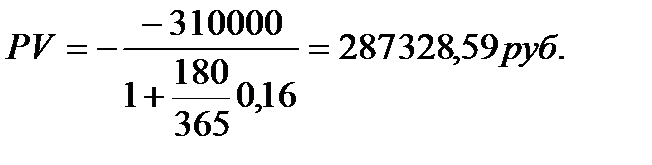
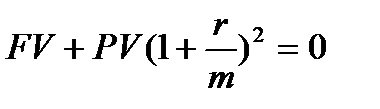
 .
.