| Понятия
| Содержание
|
| Комплексное число z
| Выражение вида z=x+iy (алгебраическая форма), i2 = -1, x;y  x=Re z, y=Im z
x=Re z, y=Im z
|
| Тригонометрическая форма комплексного числа
|  модуль и аргумент комплексного числа модуль и аргумент комплексного числа
|
| Показательная форма комплексного числа
| 
|
| Функция комплексного переменного w=f(z)
| Зависимость, при которой каждому 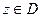 по некоторому правилу поставлено в соответствие значение по некоторому правилу поставлено в соответствие значение  u(x;y)+iv(x;y)=u+iv u(x;y)+iv(x;y)=u+iv
|
| Предел функции f(z) в точке zo
| (По Коши) число wo, если для любого положительного числа ε найдется положительное число δ, то при всех z≠zo: |z-zo|<δ выполняется неравенство |f(z)-wo|< ε
|
| Понятие
| Содержание
|
| w=f(z) непрерывная в точке zo
| Если существует предел функции в этой точке и он равен значению функции в этой точке: 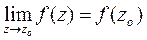
|
| Производная функции w=f(z) в точке z
| Предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю: 
|
| Дифференциал функции w=f(z) в точке z
| главная часть приращения функции:

|
| Условие Коши – Римана
| условие дифференцируемости функции w=f(z) в точке z :
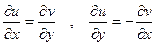
|
| Аналитичная (голоморфная) функция w=f(z) в точке z
| Если она дифференцируема в точке zo и некоторой ее окрестности (выполнены условия Коши – Римана)
|
| Числовой ряд в комплексной плоскости
| Это ряд, членами которого являются комплексные числа 
|
| Понятия
| Содержание
|
| Предмет теории вероятности
| Изучение закономерностей, возникающих при массовых, однородных явлениях
|
| Стохастический эксперимент (опыт, испытание)
| Эксперимент, результат которого заранее (до его проведения) предугадать нельзя
|
| Элементарные события
Пространство элементарных событий
| Простейшие неразложимые результаты опыта: ωi;
совокупность элементарных событий W
|
| Случайное событие
| Явление, которое может произойти или не произойти в результате стохастического эксперимента
|
| Достоверное событие
| Событие, которое обязательно наступает в результате испытания: Ω
|
| Понятие
| Содержание
|
| Невозможное событие
| Событие, которое не может произойти в результате испытания: Æ
|
| Сумма (объединение) событий А и В
| Новое событие С=А+В (С=АUВ), происходящее тогда и только тогда, когда происходит или А или В
|
| Произведение (пересечение) событий А и В
| Новое событие  (С=А∩В), происходящее тогда и только тогда, когда происходит и А и В одновременно (С=А∩В), происходящее тогда и только тогда, когда происходит и А и В одновременно
|
| Разность событий А и В
| Новое событие С=А\В, происходящее тогда и только тогда, когда происходит А, но не происходит В
|
Событие 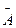 противоположно к А противоположно к А
| Если оно происходит тогда и только тогда, когда А не происходит и А+ 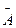 =Ω =Ω
|
| Несовместные события
| Если их одновременное появление в опыте невозможно:  Ǿ Ǿ
|
| Относительная частота события А
| Отношение  – числа m экспериментов, в которых событие А произошло к количеству проведенных экспериментов n – числа m экспериментов, в которых событие А произошло к количеству проведенных экспериментов n
|
| Классическая схема теории вероятностей
| Схема, где присутствует стохастический эксперимент, пространство элементарных событий которого состоит из конечного n числа равновозможных элементов
|
| Классическое определение вероятности события А
| Отношение числа исходов, благоприятствующих А, к общему числу несовместимых равновозможных исходов эксперимента, образующих полную группу: 
|
| Независимые случайные события А и В
| Если наступление события А не изменяет вероятности появления события В: р(В/А)=р(В)
|
| Полная группа событий
| Совокупность событий H1, H2,…,Hn таких, что H1∩H2=Ǿ, i≠j и H1UH2…UHn= Ω достоверное событие
|
| Случайная величина (СВ)
| Величина, численное значение которой может меняться в зависимости от результата стохастического эксперимента
|
| Дискретная случайная величина (ДСВ)
| Величина, возможные значения которой образуют или конечное множество или счетное
|
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.

