| Понятие
| Содержание
|
| Числовые множества
| N={1;2;…;n;…} – множество натуральных чисел
Z={0;±1; ;±2;… ;±n…} – множество целых чисел
Q={  |m |m 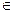 Z,n Z,n 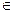 N } – множество рациональных чисел
R=Q+I, I – множество иррациональных чисел, R – множество действительных чисел N } – множество рациональных чисел
R=Q+I, I – множество иррациональных чисел, R – множество действительных чисел
|
| Функция y=f(x)
| Зависимость f, при которой каждому x 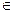 D ставится в соответствие единственное значение y D ставится в соответствие единственное значение y 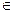 E E
|
| Числовая последовательность xn
| Функция, заданная на множестве натуральных чисел xn=f(n)
|
| Предел числовой последовательности xn
| Число а, если для любого положительного числа ε найдется такое натуральное число N, что при всех n>N выполняется | xn – а|< ε.
Записывают 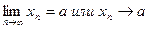
|
| Сходящаяся числовая последовательность
| Имеет предел, причем всегда единственный
|
| Расходящаяся числовая последовательность
| Не имеет предела
|
Предел функции f(x) в точке xo, т.е. 
| (По Коши) число А, если для любого положительного числа ε найдется положительное число δ, что при всех x: |x-xo|< δ, x≠xo выполняется неравенство |f(x)-A|< ε;
(по Гейне) число А, если для любой последовательности xn, n 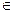 N (xn≠xo): N (xn≠xo):  выполняется выполняется 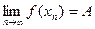
|
| Бесконечно большая функция f(x) при x→x0
| Если для любого числа М > 0 существует число δ > 0, что для всех x: |x-xo|<δ, x≠xo выполняется неравенство |f(x) |>M
Записывают: 
|
| Понятие
| Содержание
|
| Ограниченная функция
| Если существует число М > 0, что 
|
| Неопределенности
| Ситуации, когда после подстановки предельного значения получаем 
|
| Первый замечательный предел
| 
|
| Второй замечательный предел
| 
|
| y=f(x) непрерывная в точке xo
| Если существует предел функции в этой точке и он равен значению функции в этой точке: 
|
| Точки разрыва функции y=f(x)
| Точки, в которых нарушается непрерывность функции
|
| Приращение аргумента x в точке x0
| Разность двух значений аргумента 
|
| Приращение функции f(x) в точке x0
| Разность соответствующих значений функции 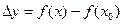
|
| Производная функции y=f(x) в точке x
| Предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю: 
|
| Дифференцирование
| Операция нахождения производной функции
|
| Логарифмическое дифференцирование
| Операция дифференцирования предварительно прологарифмированной функции
|
| Дифференциал функции y=f(x) в точке x
| Главная часть приращения функции:

|
| Правило Лопиталя
| Способ раскрытия неопределенностей вида  , основанный на применении производных , основанный на применении производных
|
| Понятие
| Содержание
|
| Функция y=f(x), возрастающая на (а;b)
| Если большему значению аргумента соответствует большее значение функции, т.е. 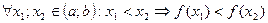
|
| Функция y=f(x), убывающая на (а;b)
| Если большему значению аргумента соответствует меньшее значение функции, т.е. 
|
| Точка максимума функции y=f(x)
| Точка xо, если сущестствует δ-окрестность точки x0 , что для всех x≠xo из этой окрестностивыполняется f(x)<f(xo)
|
| Точка минимума функции y=f(x)
| Точка xо, если сущестствует δ-окрестность точки x0, что для всех x≠xo из этой окрестностивыполняется f(x)>f(xo)
|
| Выпуклый вниз (вогнутый) график y=f(x) на (а;b)
| Если график функции расположен выше любой его касательной на этом интервале
|
| Выпуклый вверх (выпуклый) график y=f(x) на (а;b)
| Если график функции расположен ниже любой его касательной на этом интервале
|
| Точка перегиба
| Точка графика непрерывной функции, отделяющая части разного вида выпуклости
|
| Асимптота кривой
| Прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении ее от начала координат по кривой
|
| Понятие
| Содержание
|
| Дробно-рациональная функция (рациональная дробь)
| Функция, равная отношению двух многочленов: 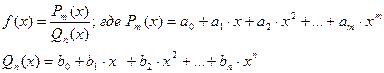
|
| Правильная рациональная дробь
Неправильная рациональная дробь
| m<n;

|
| Простейшие рациональные дроби I, II, III, IV типов
| (I)  , (II) , (II)  (III) (III)  (IV)
(IV) 

|
| Определенный интеграл
от f(x) на [a;b]
| Число I, как предел интегральной суммы, не зависящий ни от способа разбиения отрезка [a;b] на частичные отрезки, ни от выбора в них точек 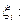

|
| Несобственные интегралы
| Определенные интегралы от непрерывной функции, но с бесконечным промежутком интегрирования или определенный интеграл с конечным промежутком интегрирования, но от функции, имеющей на нем бесконечный разрыв
|
| Двойной интеграл от функции f(x;y)по области D
| Число I как предел интегральной суммы, не зависящий ни от способа разбиения области D на части, ни от выбора в них точек 

|
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.

