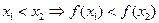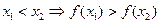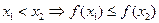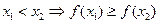|
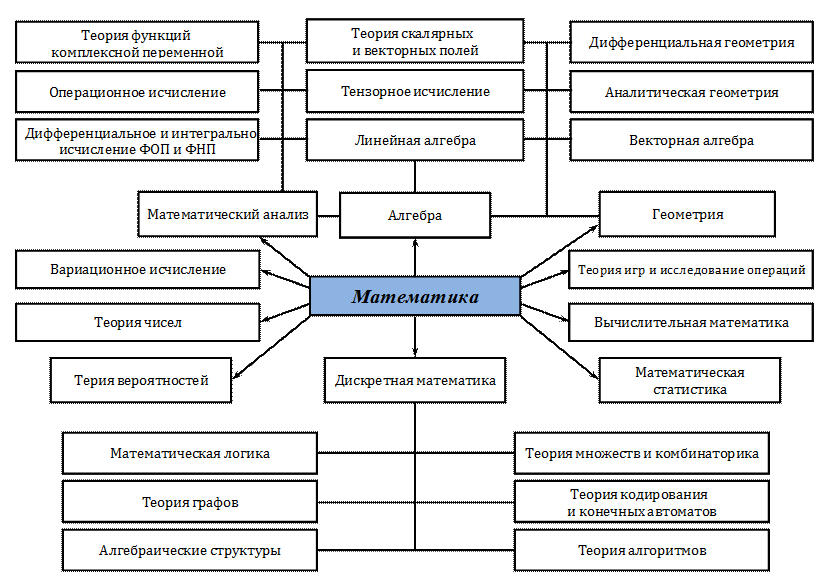
Основные разделы современной математики
Числовые множества
| Обозначение
| Определение
| Название
| | N
| {1;2;3;…;n;…}
| Множество натуральных
чисел
| | Z
| {0;±1;±2;…;±n;…}
| Множество целых чисел
| | Q
| {  | m | m 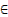 Z ,n Z ,n 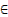 N} N}
| Множество рациональных чисел
| | I
| Бесконечная непериодическая дробь
| Множество иррациональных чисел
| | R
| R=Q 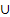 I I
| Множество действительных чисел
| | C
| {x+yi | x,y 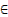 R, R, 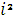 = =  1} 1}
| Множество комплексных чисел
|  
1.3. Числовые промежутки
| Обозначение
| Определение
| Название
| Изображение
| | [a;b]
| {x 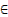 R| a≤x≤b} R| a≤x≤b}
| Отрезок
| 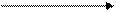            a b x
a b x
| | (a;b)
| {x  R| a<x<b} R| a<x<b}
| интервал
|       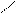      a b x
a b x
| | (a;b]
[a;b)
| {x 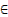 R| a<x≤b}
{x R| a<x≤b}
{x 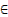 R| a≤x<b} R| a≤x<b}
| Полуинтервал
|             a b x
a b x
            a b x
a b x
| | [a;+∞)
(-∞;b]
| {x 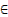 R| x≥a}
{x R| x≥a}
{x 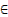 R| b≤x} R| b≤x}
| Луч
или
закрытый луч
|           a x
a x
 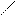  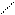   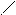     b x
b x
| | (a;+∞)
(-∞;b)
| {x 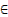 R| x>a}
{x R| x>a}
{x 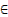 R| x<b} R| x<b}
| Открытый луч
|        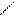    a x
a x
 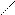        
 b x
b x
| | (-∞;+∞)
| {x 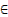 R| R| 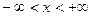 } }
| Бесконечный интервал
|     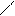 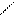   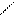 
 x x
| |
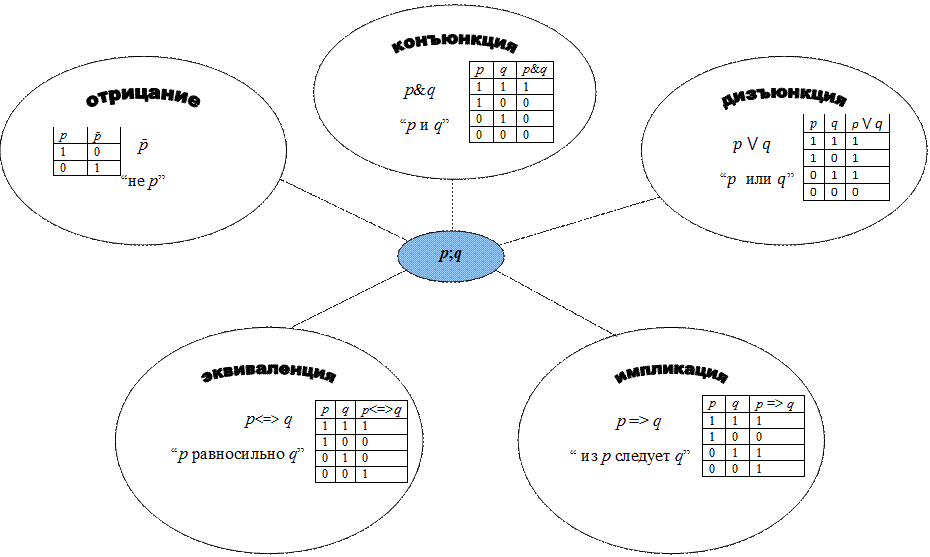
Логические операции над высказываниями
Множества и операции над ними

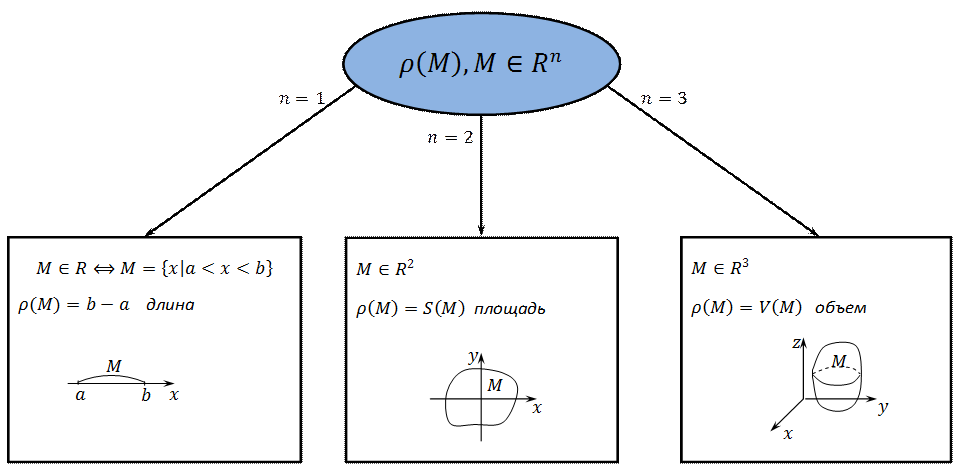
Мера множества
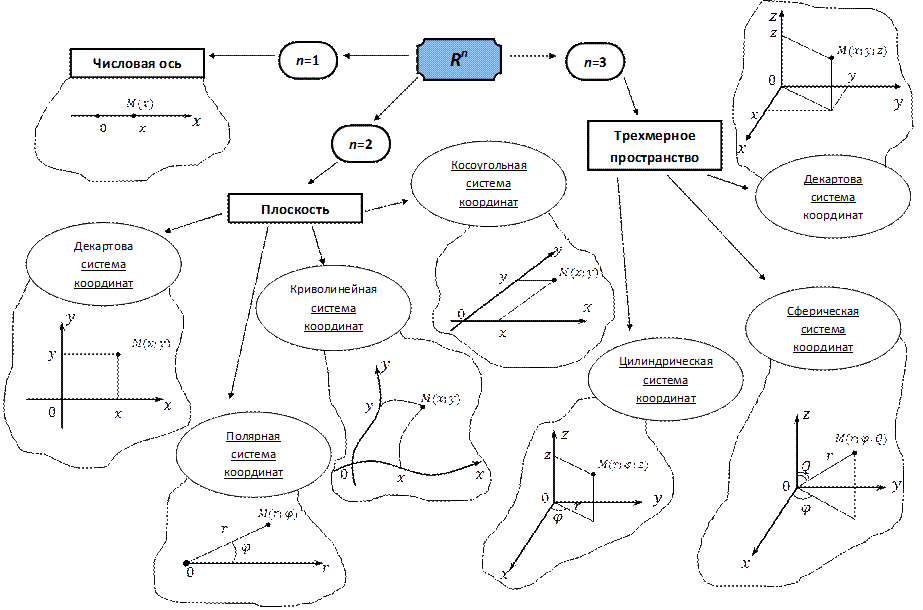
Системы координат
Классификация функций

Свойства и графики некоторых элементарных функций
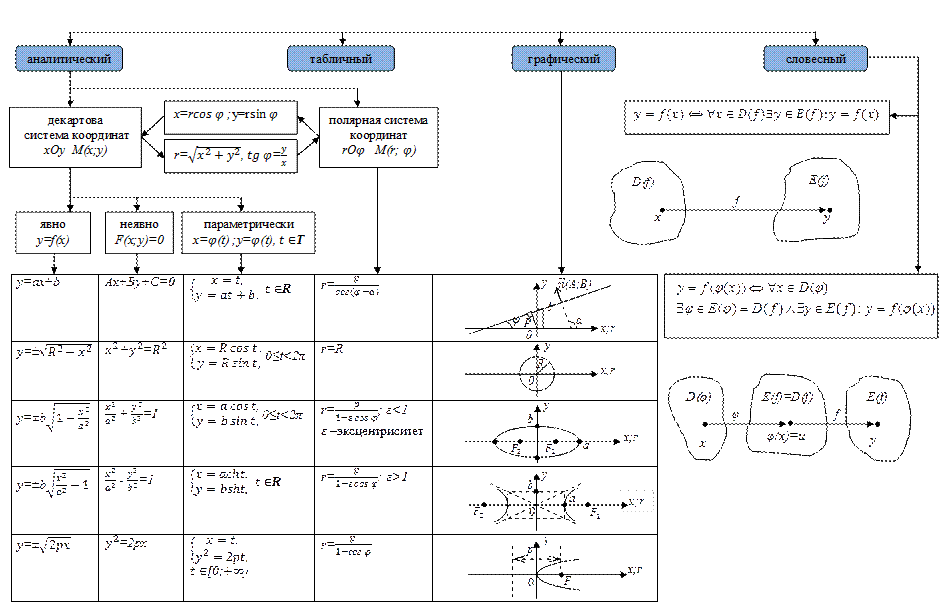
1.10. Способы задания функции в R2
Основные характеристики функции
|


 | m
| m 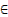 Z ,n
Z ,n 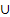 I
I
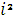 =
=  1}
1}



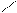


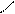



 a b x
a b x




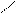



 a b x
a b x









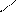 a b x
a b x












 a x
a x




 b x
b x





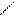

 a x
a x

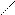



 b x
b x
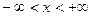 }
}
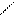



 x
x





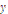
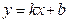

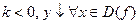



 x
x
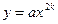 , kÎN
, kÎN
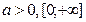
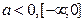


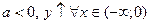
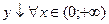


 y y
y y 


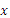




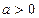
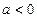
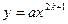 , kÎN
, kÎN
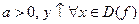
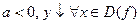







 y
y 

 ,
, 
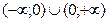
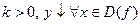





 y y
y y

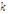
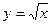
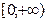
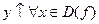
 y
y


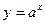 ,
a>0, a≠1
,
a>0, a≠1
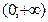
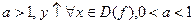




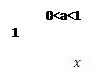
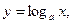 a>0, a≠1
a>0, a≠1



 y y
y y

 nÎZ
nÎZ
 y
y
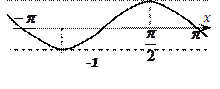
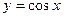

 nÎZ
nÎZ
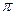






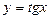
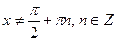







 y
y
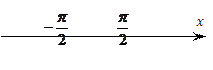
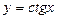
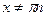 ,
, 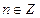
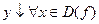




 y
y

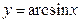
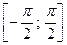


 y
y


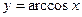

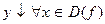



 y
y

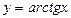
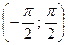
 y
y
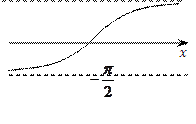


 y
y
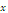


 гиперболический синус
гиперболический синус
 y
y

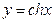
 гиперболический косинус
гиперболический косинус
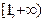
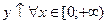
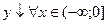

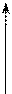 y
y
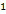


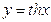
 гиперболический тангенс
гиперболический тангенс
 y
y

 1
1

 -1
-1
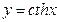
 гиперболический котангенс
гиперболический котангенс


 y
y
 1
1


 -1
-1 ареасинус
ареасинус
 y
y


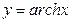 ареокосинус
ареокосинус

 y
y

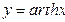 ареотангенс
ареотангенс



 y
y
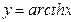 ареокотангенс
ареокотангенс



 y
y


 D={
D={  :
: 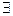 y=f(x)}
y=
y=f(x)}
y= 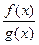
 D={
D={ 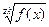 =D={
=D={  D={
D={ 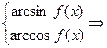 D={
D={ 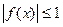 }
}





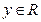 : y=f(x), x
: y=f(x), x 









 : f(x)=0
: f(x)=0
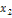
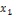







 f(-x)=f(x)
2) y=f(x) – нечетная
f(-x)=f(x)
2) y=f(x) – нечетная 









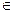 D
D 








 :
: