|
Дифференциальные уравнения
| Понятие
| Содержание
| | Дифференциальное уравнение (ДУ)
| Уравнение, связывающее независимую переменную, искомую функцию и ее производные
| | Решение ДУ
| Функция, которая при подстановке в уравнение обращает его в верное тождество
| | Порядок ДУ
| Порядок наивысшей производной, входящей в ДУ
| | ДУ первого порядка
| Уравнение, связывающее независимую переменную, искомую функцию и ее производную: 
| | Общее решение ДУ первого порядка
| Функция 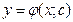 , которая является решением ДУ при каждом с (с=const), и для любого допустимого начального условия , которая является решением ДУ при каждом с (с=const), и для любого допустимого начального условия  константа константа 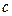 определяется однозначно определяется однозначно
| | Частное решение ДУ первого порядка
| Функция 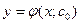 , полученная из общего решения , полученная из общего решения 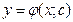 при конкретном значении постоянной с=с0 при конкретном значении постоянной с=с0
| | ДУ с разделяющимися переменными
| Уравнение вида: 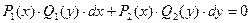
| | Однородная функция n-го порядка
| Если при умножении каждого ее аргумента на множитель 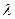 вся функция умножится на вся функция умножится на 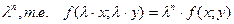
| | Однородное ДУ первого порядка
| Уравнение  , если функция f(x;y ) – однородная нулевого порядка. , если функция f(x;y ) – однородная нулевого порядка.
| | Линейное ДУ первого порядка
| Уравнение вида: 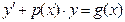
| | Уравнение Бернулли
| уравнение вида: 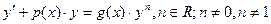
| | ДУ второго порядка
| Уравнение вида:

| | Общим решением ДУ второго порядка
| Функция 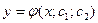 , которая является решением ДУ при каждом с1; с2 (с1; с2 – const) и для любого допустимого начального условия , которая является решением ДУ при каждом с1; с2 (с1; с2 – const) и для любого допустимого начального условия 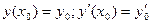 константы константы 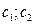 определяются однозначно определяются однозначно
| | Понятие
| Содержание
| | Интегральная кривая ДУ
| График всякого решения ДУ
| | ДУ n-го порядка
| Уравнение вида: 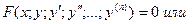 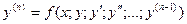
| | Общее решение ДУ
n-го порядка
| Функция  , которая является решением ДУ при каждом наборе значений констант с1;с2;…;сn, определяемых однозначно для каждого набора допустимых начальных условий , которая является решением ДУ при каждом наборе значений констант с1;с2;…;сn, определяемых однозначно для каждого набора допустимых начальных условий
| | Задача Коши ДУ n-го порядка
| Задача нахождения решения ДУ 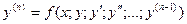 , удовлетворяющего заданным начальным условиям: , удовлетворяющего заданным начальным условиям: 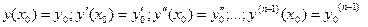
| | ЛОДУ n-го порядка с постоянными коэффициентами
| уравнение вида
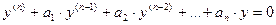
| | ЛОДУ второго порядка с постоянными коэффициентами
| 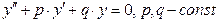
| | Характеристическое уравнение ДУ
| 
| | Линейные неоднородные ДУ
второго порядка (ЛНДУ)
| 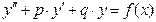
| | Специальная правая часть ЛНДУ
|  
|
Ряды
| Понятие
| Содержание
| | Числовой ряд
| Выражение вида: 
| | Частичная сумма ряда
| Сумма первых n членов ряда: 
|
| Понятие
| Содержание
| | Ряд сходится
| Если существует конечный предел последовательности частичных сумм ряда: 
| | Ряд расходится
| Если  не существует или не существует или 
| | Знакочередующийся ряд
| Ряд вида 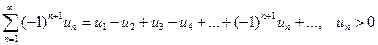
| | Ряд абсолютно сходится
| Если сходится ряд, составленный из модулей его членов
| | Ряд условно сходится
| Если сам ряд сходится, а ряд, составленный из модулей его членов, расходится
| | Функциональный ряд
| Ряд, членами которого являются функции от x:

| | Степенной ряд
| ряд, члены которого – степенные функции аргумента x: 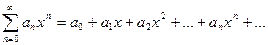 или
или 
| | Область сходимости
| Совокупность числовых значений аргумента x, при которых функциональный ряд сходится
| Тригонометрический ряд на отрезке 
| Функциональный ряд вида:
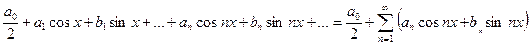
| Коэффициенты Фурье функции f(x) на отрезке 
| Числа 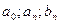 , определяемые по формулам: , определяемые по формулам: 
|
Элементы теории поля
| Понятие
| Содержание
| | Поле
| Область V пространства, в каждой точке которой определено значение некоторой величины
| | Скалярное поле
| Область пространства, каждой точке M которой соответствует определенное число: U=U(M)
| | Векторное поле
| Область пространства, каждой точке M которой соответствует некоторый вектор 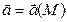
| Производная функции U=U(M) вточке М понаправлению 
| 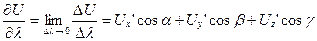 характеризует скорость изменения функции поля в точке М по направлению
характеризует скорость изменения функции поля в точке М по направлению 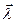
| | Градиент функции U=U(M)
| Вектор, координатами которого являются значения частных производных функции U(x;y;z) в точке M(x;y;z): 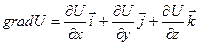 указывает направление
указывает направление 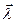 , в котором , в котором 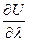 имеет наибольшее значение имеет наибольшее значение
| Поток вектора 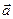 через поверхность S через поверхность S
| Интеграл по поверхности от скалярного произведения вектора поля на единичный вектор нормали к поверхности:
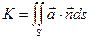
| | Дивергенция векторного поля в точке М
| Предел отношения потока поля через замкнутую поверхность S, окружающую точку М, к объему тела, ограниченного этой поверхностью, при условии, что вся поверхность стягивается в точку М 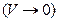 : : 
|
| Понятие
| Содержание
| Циркуляция вектора 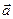 вдоль L вдоль L
| Криволинейный интеграл по замкнутому контуру L от скалярного произведения вектора 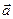 на вектор на вектор 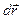 , касательный к контуру L: , касательный к контуру L: 
| Ротор вектора 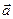 в точке М в точке М
| Вектор, проекция которого на каждое направление равна пределу отношения циркуляции вектора 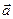 по контуру L плоской площадки S, перпендикулярной этому направлению, к площади этой площадки по контуру L плоской площадки S, перпендикулярной этому направлению, к площади этой площадки
| | Оператор Гамильтона
| Символический вектор 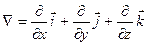
| | Соленоидальное поле
| Векторное поле во всех точках которого дивергенция равна нулю: 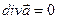
| | Потенциальное поле
| Векторное поле во всех точках которого ротор равен нулю: 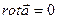
| | Гармоническое поле
| Векторное поле одновременно соленоидальное и потенциальное: 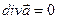 и и 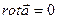
|
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

