
|
|
Глава I. Некоторые положения элементарной математикиМинистерство образования и науки Российской Федерации Костромской государственный технологический университет О.Р. Воронцова, О.Б. Садовская СТУКТУРНО-ТЕМАТИЧЕСКИЕ КАРТЫ ПО ВЫСШЕЙ МАТЕМАТИКЕ Рекомендовано редакционно-издательским советом университета в качестве учебного пособия
Кострома КГТУ УДК 510(022) Воронцова О.Р. Структурно – тематические карты по высшей математике: учебное пособие/ О.Р. Воронцова, О.Б. Садовская. – Кострома: Изд-во Костромского государственного технологического университета, 2010. – 174 с.
В учебном пособии, которое соответствует ГОС ВПО и учебной программе технического вуза, курс высшей математики представлен в виде структурно-тематических карт. Предлагаемая форма удобна для лучшего усвоения весьма абстрактного материала непростой учебной дисциплины. Настоящее пособие предназначено для студентов и преподавателей вузов. Оно может оказать помощь при подготовке к занятиям, контрольным и самостоятельным работам. Предложенная форма изложения материала – в виде таблиц, схем – позволяет систематизировать знания, облегчает понимание сложных определений, понятий и формул.
Рецензенты: д.п.н., профессор Е.И. Смирнов (кафедра «Математического анализа», ЯГПУ) д.э.н., профессор Е.М. Скаржинская (кафедра «Математические методы в экономике», КГУ)
© Костромской государственный технологический университет, 2010
Оглавление Предисловие. 11 Глава I. Некоторые положения элементарной математики. 3 1.1. Основные разделы современной математики. 3 1.2. Числовые множества. 3 1.3. Числовые промежутки. 3 1.4. Логические операции над высказываниями. 3 1.5. Множества и операции над ними. 3 1.6. Мера множества. 3 1.7. Системы координат. 3 1.8. Классификация функций. 3 1.9. Свойства и графики некоторых элементарных функций. 3 1.10. Способы задания функции в R2 3 1.11. Основные характеристики функции. 3 1.12. Преобразование графиков функций в декартовой системе координат. 3 1.13. Обратная функция. 35 1.14. Значения тригонометрических функций от обратных. 36 1.15. Некоторые значения тригонометрических функций для углов I четверти. 37 1.16. Связь тригонометрических функций одного аргумента. 37 Глава II. Элементы линейной алгебры и аналитической геометрии. 38 2.1. Вычисление определителя. 38 2.2. Виды СЛАУ.. 39 2.3. Методы решения СЛАУ.. 40 2.4. Действия над векторами и их приложения. 41 2.5. Способы задания прямой линии на плоскости. 42 2.6. Исследование поведения прямой линии на плоскости. 43 2.7 Острый угол между прямыми в пространстве R2 44 2.8. Кривые второго порядка. 3 2.9. Выделение полного квадрата или приведение параболы к каноническому виду. 46 2.10. Виды задания прямой линии в пространстве R3 47 2.11. Плоскость в пространстве R3 48 2.12. Взаимное расположение прямых l1, l2 и плоскостей p1, p2 в R3 49 Глава III. Основы математического анализа. 50 3.1. Связь основных понятий теории предела переменной. 50 3.2. Расширение понятия предела с функции натурального на функцию действительного аргумента. 51 3.3. Предел функции. 52 3.4. Отсутствие предела функции. 53 3.5. Односторонние пределы функции f(x) в точке a. 54 3.6. Действия с бесконечно малыми величинами. 55 3.7. Основные пары эквивалентных б. м. ф. при x®a. 56 3.8. Сводная таблица применения основных теорем о пределах, б.м.в. и б.б.в. 57 3.9. Технология вычисления пределов функций. 58 3.10. Непрерывность функции в точке. 59 3.11. Разрывы функции. 60 Глава IV. Дифференциальное исчисление ФОП.. 3 4.1. Формы представления учебного элемента «Производная». 3 4.2. Производная функции и ее частные случаи. 62 4.3. Техника дифференцирования. 63 4.4. Геометрический и физический смысл производной функции. 64 4.5. Экстремумы функции одной переменной. 65 4.6. Необходимое условие экстремума функции одной переменной. 66 4.7. Дифференциал ФОП.. 67 4.8. Производные и дифференциалы высших порядков ФОП.. 67 4.9. Нахождение экстремумов функции одной переменной. 68 4.10. Полное исследование функции. 69 Глава V. Элементы ФОП, ФНП и ФКП.. 70 5.1. Комплексные числа. 70 5.2. Действия над комплексными числами. 71 5.3. Основные функции комплексной переменной. 72 5.4. Функция одной и нескольких переменных. 75 5.5. Простейшие поверхности второго порядка. 76 5.6. Расширение понятия предела с функции одной на функцию двух переменных. 77 5.7. Предел функции одной и нескольких действительных переменных и комплексной. 78 5.8. Частные производные функции двух переменных. 79 5.9. Дифференцирование функции одной и нескольких действительных переменных и комплексной. 80 5.10. Производные и дифференциалы высших порядков функций одной и двух переменных. 81 5.11. Локальные экстремумы функции одной и двух переменных. 82 5.12. Методы определения локальных экстремумов функций одной и двух переменных. 83 5.13. Абсолютные экстремумы функции двух переменных. 84 5.14. Дифференцирование функций комплексной переменной. 85 5.15. Понятие ε-окрестности действительной в Rn и комплексной точки. 86 Глава VI. Интегральное исчисление ФОП.. 87 6.1. Основные методы интегрирования. 87 6.2. Замена в неопределенном интеграле. 88 6.3. Интегрирование функций, содержащих квадратный трехчлен. 89 6.4. Метод интегрирования по частям. 90 6.5. Дробно-рациональная функция и ее интегрирование. 91 6.6. Интегрирование тригонометрических функций. 92 6.7. Интегрирование иррациональных выражений. 93 6.8. «Берущиеся» и «неберущиеся» интегралы.. 94 6.9. Примеры «неберущихся» интегралов. 95 6.10. Итоговая таблица основных методов интегрирования. 96 Глава VII. Определенное и несобственное интегрирование. Элементы теории поля. 102 7.1. Вычисление определенного интеграла. 102 7.2. Несобственные интегралы.. 103 7.3. Криволинейные интегралы.. 104 7.4. Технология вычисления двойного интеграла. 105 7.5. Технология вычисления площадей и объемов тел вращения. 106 7.6. Замена в двойном и тройном интегралах. 108 7.7. Технология вычисления тройного интеграла. 109 7.8. Сводная таблица вычисления поверхностных интегралов. 110 7.9. Основные характеристики скалярных и векторных полей в R3 111 7.10. Операторы Гамильтона, Лапласа и основные свойства полей. 112 7.11. Нахождение массы объектов с переменной плотностью.. 113 7.12. Обобщение основных свойств определенных интегралов. 114 7.13. Приложения кратных интегралов. 115 Глава VIII. Обыкновенные дифференциальные уравнения. Элементы операционного исчисления. 117 8.1. Дифференциальные уравнения первого порядка. 117 8.2. Дифференциальные уравнения второго порядка, допускающие понижение порядка. 118 8.3. Структура решения дифференциального уравнения, допускающих понижение порядка. 119 8.4. Структура решения линейного неоднородного дифференциального уравнения с постоянными коэффициентами. 120 8.5. Разновидности частных решений линейного неоднородного дифференциального уравнения в зависимости от формы специальной правой части. 121 8.6. Линейное однородное дифференциальное уравнение n-го порядка с постоянными коэффициентами. 122 8.7. Сводная схема решения основных типов обыкновенных дифференциальных уравнений. 123 8.8. Основные правила и формулы операционного исчисления. 124 8.9. Решение ДУ операционным методом. 125 Глава IX. Ряды.. 126 9.1. Признаки сходимости знакоположительных рядов. 126 9.2. Абсолютная и условная сходимость знакочередующихся рядов. 127 9.3. Степенные ряды (ряды по степеням (x – x0)) 128 9.4. Разложение функций в ряд Маклорена. 129 9.5. Основные приложения рядов Тейлора и Маклорена. 130 9.6. Основная тригонометрическая система функций (ОТСФ) и ее частные случаи. 131 9.7. Критерии сходимости. 132 9.8. Ряды Фурье. 133 9.9. Виды рядов. 134 Глава X. Элементы теории вероятной и математической статистики. 135 10.1. Соответствие терминов теории множеств и теории вероятностей. 135 10.2. Элементы комбинаторики. 136 10.3. Основные теоремы теории вероятности. 137 10.4. Повторные испытания Бернулли (бинарная схема) 138 10.5. Технология нахождения вероятности события. 139 10.6. Случайные величины.. 140 10.7. Основные распределения и их числовые характеристики. 141 10.8. Соответствие терминов, обозначений и формул случайной величины и вариационного ряда. 142 10.9. Алгоритм проверки гипотез о законе распределения случайных величин. 143 10.10. Схема применения критерия χ2 для проверки гипотезы о нормальном законе распределения С.В. X.. 144 Глава XI. Вычислительная математика. 145 11.1. Методы решения СЛАУ.. 146 11.2. Приближенные методы решения нелинейных уравнений. 147 11.3. Модели подбора эмпирической функции по экспериментальным данным. 148 11.4. Алгоритмы решения нелинейных уравнений. 149 11.5. Оценка параметров регрессии метода наименьших квадратов. 150 11.6. Приближённое вычисление определённого интеграла. 151 ГЛОССАРИЙ.. 152 Элементы линейной алгебры.. 152 Элементы векторной алгебры.. 153 Аналитическая геометрия на плоскости. 155 Введение в математический анализ. 155 Интегральное исчисление. 158 Дифференциальные уравнения. 161 Ряды.. 162 Элементы теории поля. 164 Теория функции комплексного переменного. 165 Теория вероятностей. 166 Математическая статистика. 168
Предисловие Взяв на вооружение известную поговорку «Лучше один раз увидеть, чем сто раз услышать», мы попробовали перенести ее на процесс обучения высшей математике, создав серию структурно-тематических карт. Настоящее пособие предназначено для студентов и преподавателей вузов. Оно может оказать помощь при подготовке к занятиям, контрольным и самостоятельным работам. Предложенная форма изложение материала – в виде таблиц, схем – позволяет систематизировать знания, облегчает понимание сложных определений, понятий и формул. Структурно-тематическая карта по высшей математике – система элементов рассуждения (понятий, математических действий), обозначенных геометрическими фигурами (прямоугольник, овал, ромб и т.д.) с вложенным математическим текстом (блоком), содержащим главное на этом этапе познания. Согласно существующим между блоками логическим связям, они соединяются стрелками, направление которых показывает переход от предыдущих компонент схемы к последующим по двум принципам: или от простого к сложному или обратно – от общего к частному. Предложенный способ изложения материала позволяет: • систематизировать знания; • облегчает понимание и усвоение сложных определений, понятий и формул; • отражает существующие между ними связи; • устанавливает приоритеты; • содержит области применения. Основными преимуществами предложенного способа изложения информации являются: 1) возможность построения структурно-логических схем учебного материала различных уровней: параграфа, темы, подраздела, раздела, всего предметного курса; 2)компактная и мобильная форма систематизации знаний студентов как в процессе их получения по данной конкретной теме и ликвидации пробелов в знаниях, так и для подготовки к разнообразным видам аттестаций; 3)универсальность метода структуризации учебного материала по отношению к любой дисциплине, что при широком использовании по разным учебным предметам повысит эффективность его применения; 4)многообразие возможных форм применения структурно-логических схем, например в виде игр «Заполни ячейку», «Расставь стрелки», «Найди логическую ошибку», и т.д., способствует повышению заинтересованности обучающихся и более глубокому осмыслению ими изучаемого материала; 5)наглядность представления учебного материала; 6)легко обозримая форма подачи материала способствует более прочному быстрому, следовательно, более эффективному его осмыслению и запоминанию. Предлагаемый метод представления знаний направлен на повышение эффективности обучения высшей математике в первую очередь студентов технических специальностей, т.к. по складу мышления является им более близким. Структурно-тематические карты разработаны к следующим разделам курса высшей математики: • основы линейной алгебры и аналитической геометрии; • элементы математического анализа; • основы дифференциального и интегрального исчисления; • элементы теории функции многих переменных; • элементы теории обыкновенных дифференциальных уравнений; • теории вероятностей и математической статистики; • вычислительная математика. ОСНОВНЫЕ ОБОЗНАЧЕНИЯ N, Z, Q, I, R, C – множества натуральных, целых, рациональных, иррациональных, действительных, комплексных чисел Þ - знак логического следования (одно следует из другого)
n! - обозначение произведения
lim - знак предела
Æ - пустое множество
supA - точная верхняя грань множества А infA - точная нижняя грань множества А
D(f ) - область определения функции f E(y) -множество значений функции f
i - мнимая единица, i2=-1
Rez - действительная часть комплексного числа Imz - мнимая часть комплексного числа Argz - аргумент комплексного числа аrgz - главное значение аргумента комплексного числа
Список принятых сокращений б.б.в. – бесконечно большая величина б.м.в. – бесконечно малая величина ДВР – дискретный вариационный ряд ДСВ – дискретная случайная величина ДУ – дифференциальное уравнение ДУ с РП – дифференциальное уравнение с разделяющимися переменными ИВР – интервальный вариационный ряд ЛНДУ – линейное неоднородное дифференциальное уравнение ЛОДУ – линейное однородное дифференциальное уравнение МНК – метод наименьших квадратов НСВ – непрерывная случайная величина ОРО – общее решение однородного дифференциального уравнения ОРН – общее решение неоднородного дифференциального уравнения ОТСФ – основная тригонометрическая система функций СВ – случайная величина СЛАУ – система линейных алгебраических уравнений ФКП – функция комплексной переменной ФНП – функция нескольких переменных ФОП – функция одной переменной ЧРН – частное решение неоднородного дифференциального уравнения Глава I. Некоторые положения элементарной математики 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
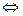 - знак равносильности
- знак равносильности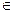 - знак принадлежности
- знак принадлежности - знак непринадлежности
- знак непринадлежности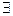 - квантор существования (соответствует словам «имеется», «найдется»)
- квантор существования (соответствует словам «имеется», «найдется»)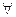 - квантор общности (соответствует словам «для любого», «для всех»)
- квантор общности (соответствует словам «для любого», «для всех») - равенство по определению
- равенство по определению - k принимает натуральные значения от 1 до n включительно
- k принимает натуральные значения от 1 до n включительно (читается «эн-факториал»)
(читается «эн-факториал») 
 - знак суммы
- знак суммы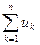 - сумма
- сумма 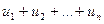
 - множество, состоящее из элементов a,b,c…
- множество, состоящее из элементов a,b,c… - бесконечная числовая последовательность с n-ым членом a
- бесконечная числовая последовательность с n-ым членом a - объединение множеств A и B
- объединение множеств A и B - пересечение множеств A и B
- пересечение множеств A и B - разность множеств A и B
- разность множеств A и B - дополнение множества А до универсального множества U
- дополнение множества А до универсального множества U - множество А подмножество множества В
- множество А подмножество множества В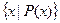 - множество элементов x, удовлетворяющих условию P(x)
- множество элементов x, удовлетворяющих условию P(x)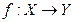 - функция f, отображающая X в (на) Y
- функция f, отображающая X в (на) Y - функция, обратная функции f, отображающая Y на X
- функция, обратная функции f, отображающая Y на X - композиция функции f и q, т.е. сложная функция, составленная из f и q
- композиция функции f и q, т.е. сложная функция, составленная из f и q - промежутки замкнутый, открытый, полуоткрытый (отрезок, интервал, полуинтервал)
- промежутки замкнутый, открытый, полуоткрытый (отрезок, интервал, полуинтервал) -
-  - окрестность точки x0
- окрестность точки x0 -
- 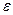 - окрестность точки а
- окрестность точки а - векторы
- векторы - базисные векторы прямоугольной декартовой системы координат
- базисные векторы прямоугольной декартовой системы координат - модуль вектора
- модуль вектора 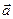
 -n - мерное евклидово пространство
-n - мерное евклидово пространство - матрицы обратная, транспонированная
- матрицы обратная, транспонированная - сопряженные комплексные числа
- сопряженные комплексные числа - модуль комплексного числа
- модуль комплексного числа - первая производная функции y=f(x)
- первая производная функции y=f(x)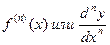 - n-ая производная функции y=f(x)
- n-ая производная функции y=f(x) -знак неопределенного интеграла
-знак неопределенного интеграла - знак определенного интеграла
- знак определенного интеграла или
или  - частные производные первого порядка функции u=f(x,y,z)
- частные производные первого порядка функции u=f(x,y,z) или
или  - частные производные второго порядка функции u=f(x,y,z)
- частные производные второго порядка функции u=f(x,y,z)