Необходимое условие экстремума функции одной переменной

| 4.7. Дифференциал ФОП
| 4.8. Производные и дифференциалы высших порядков ФОП
|

Нахождение экстремумов функции одной переменной
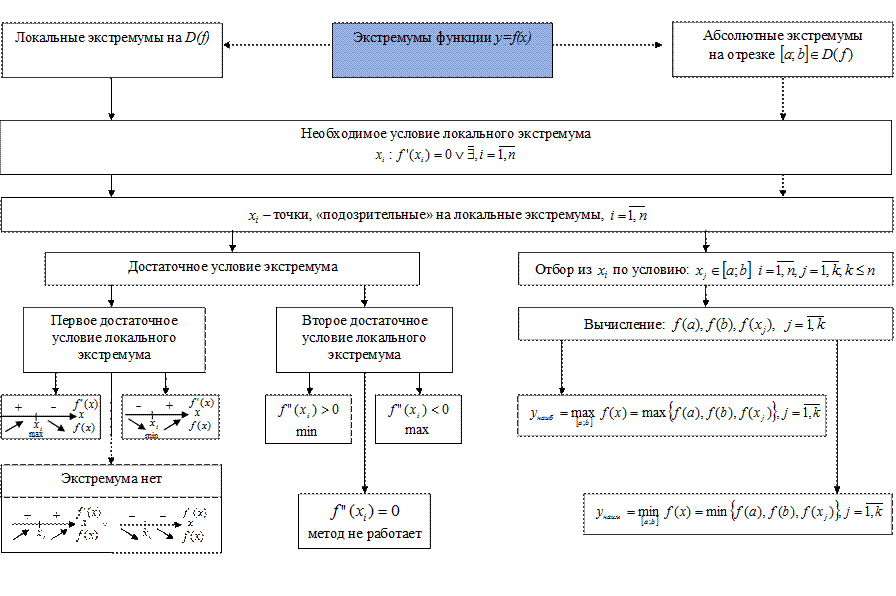
Полное исследование функции
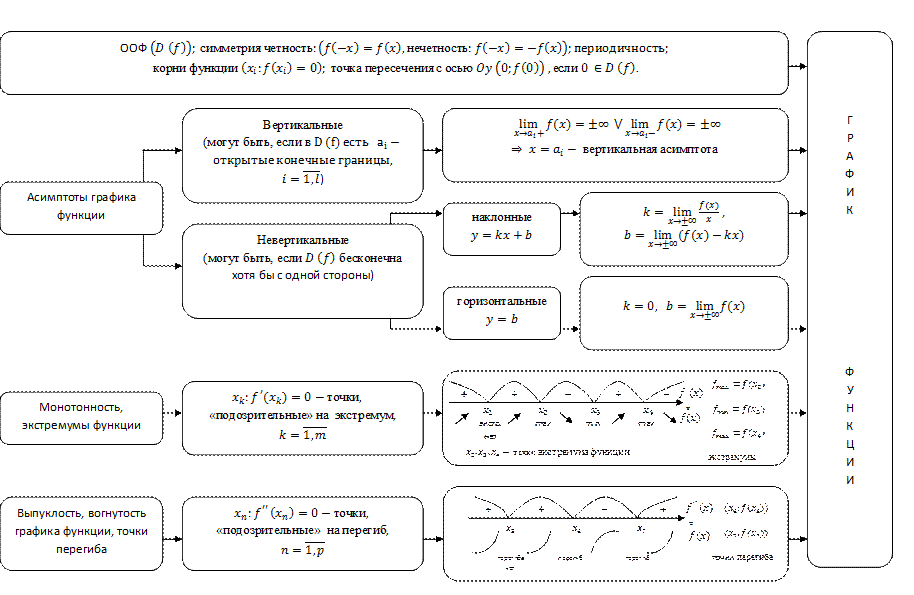
Глава V. Элементы ФОП, ФНП и ФКП
Комплексные числа

5.2. Действия над комплексными числами 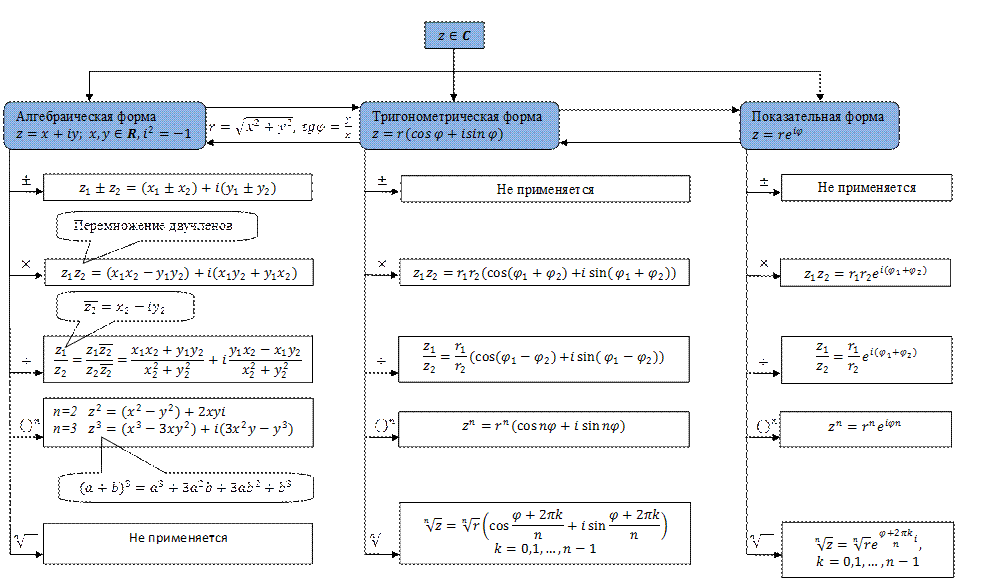
Основные функции комплексной переменной
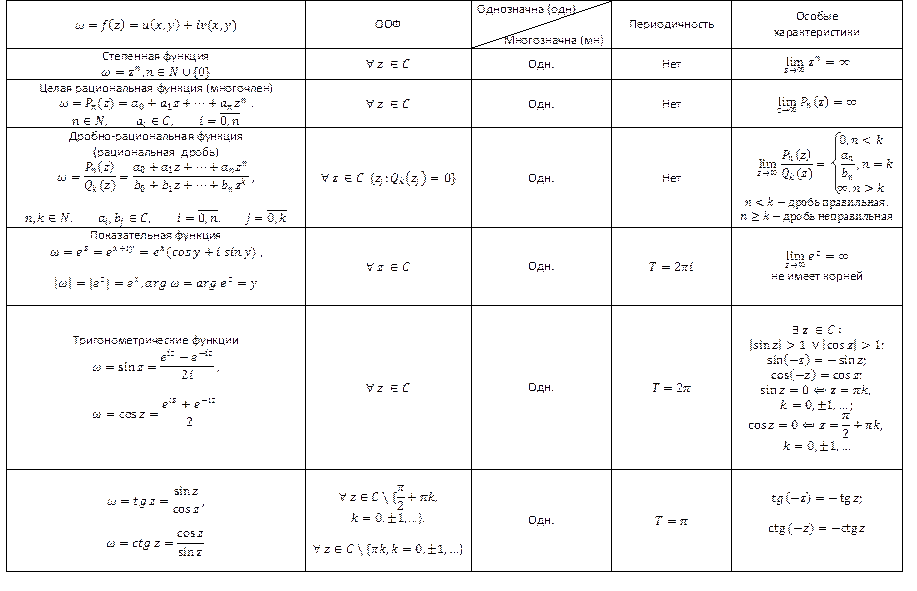
Гиперболические функции
 , ,
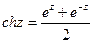
| 
| Одн.
| 
| 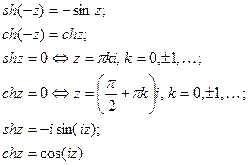
|  , ,

|

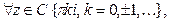
| Одн.
| 
| 
|
Логарифмическая функция
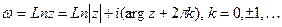
| 
| Мн.
| нет
|
Главное значение
логарифма

| Примечание: Общая степенная функция 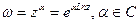
Общая показательная функция 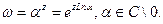
Обратные тригонометрические функции: 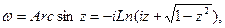  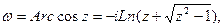  Обратные гиперболические функции: Обратные гиперболические функции: 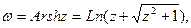   
Функция одной и нескольких переменных

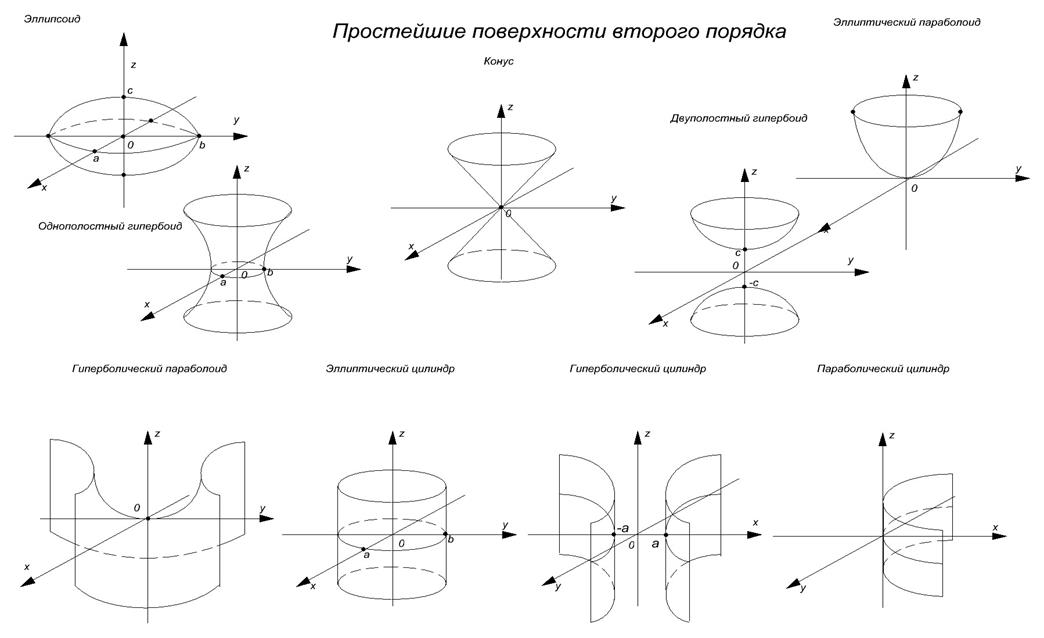 5.5. Простейшие поверхности второго порядка 5.5. Простейшие поверхности второго порядка
Расширение понятия предела с функции одной на функцию двух переменных
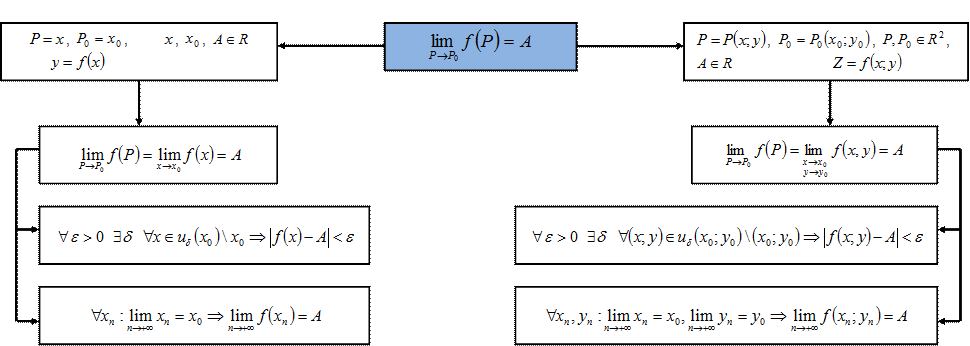
Предел функции одной и нескольких действительных переменных и комплексной

Частные производные функции двух переменных
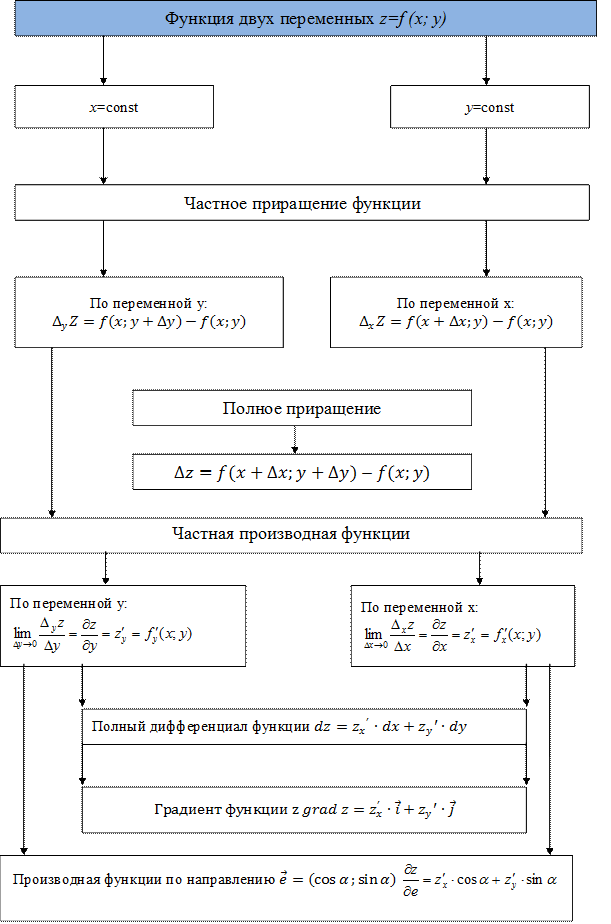
Дифференцирование функции одной и нескольких действительных переменных и комплексной

Производные и дифференциалы высших порядков функций одной и двух переменных

Локальные экстремумы функции одной и двух переменных
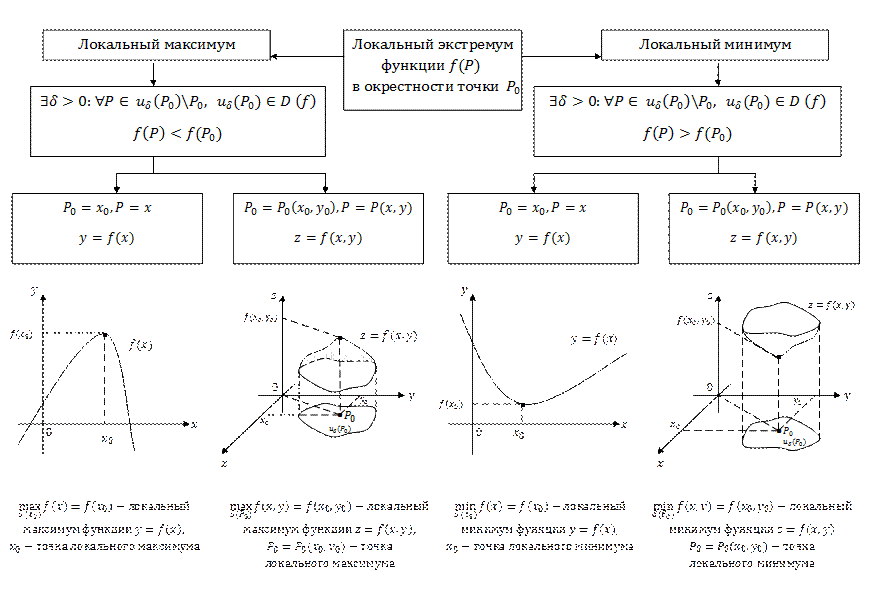
Методы определения локальных экстремумов функций одной и двух переменных

Абсолютные экстремумы функции двух переменных

Дифференцирование функций комплексной переменной

5.15. Понятие ε-окрестности действительной в Rn и комплексной точки
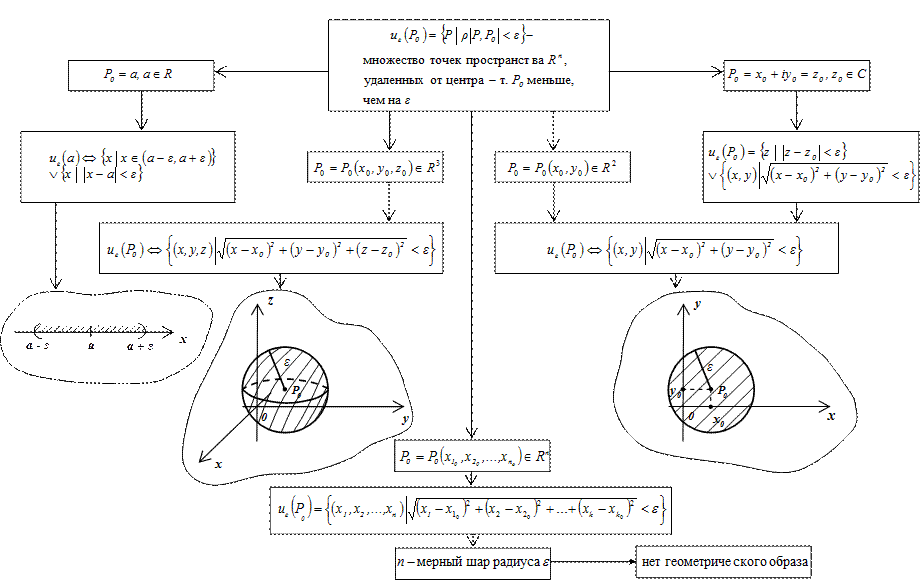
Глава VI. Интегральное исчисление ФОП
Основные методы интегрирования

Замена в неопределенном интеграле
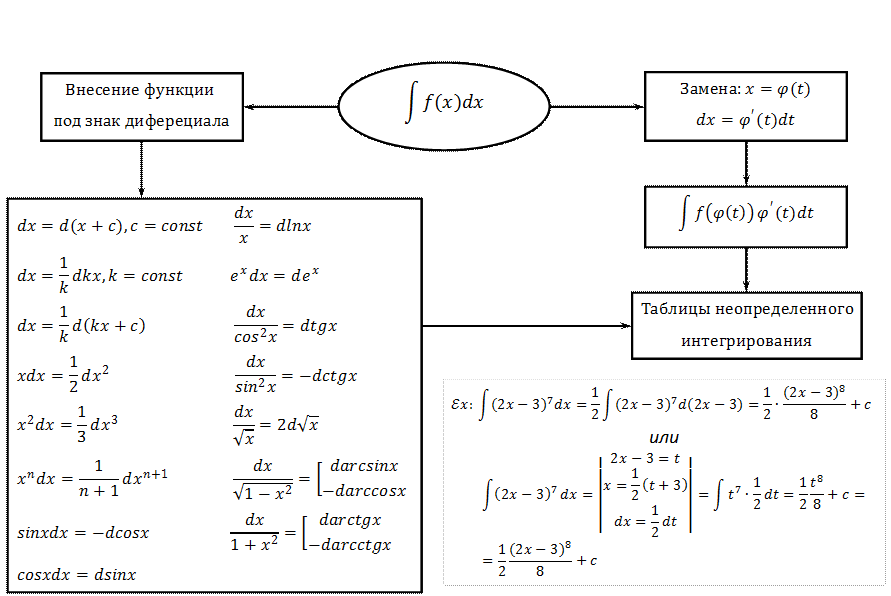
Интегрирование функций, содержащих квадратный трехчлен
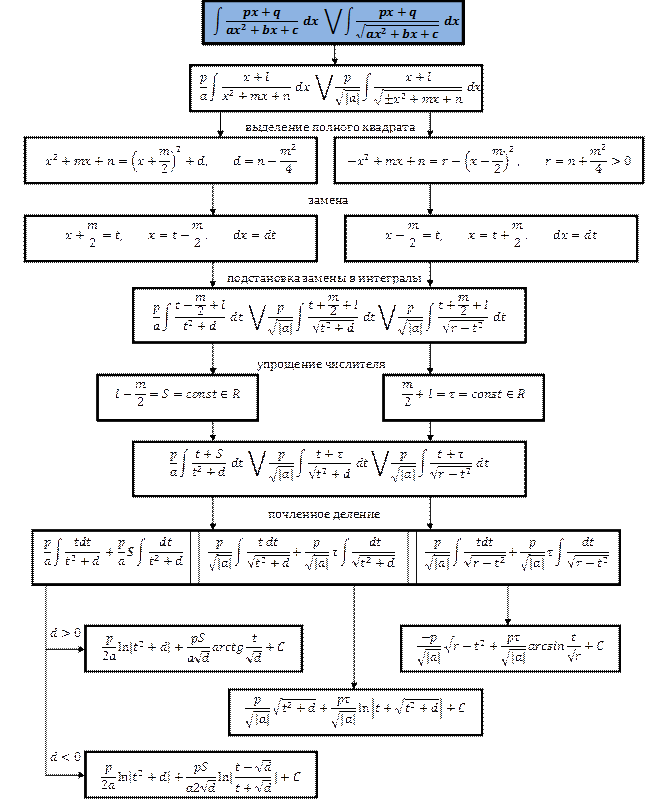
Метод интегрирования по частям

Дробно-рациональная функция и ее интегрирование

Интегрирование тригонометрических функций
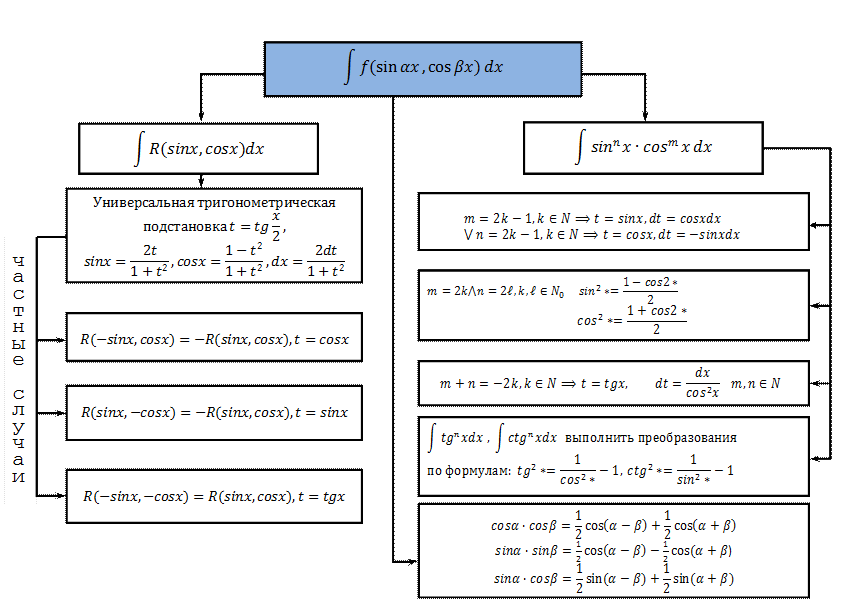
Интегрирование иррациональных выражений

Берущиеся» и «неберущиеся» интегралы
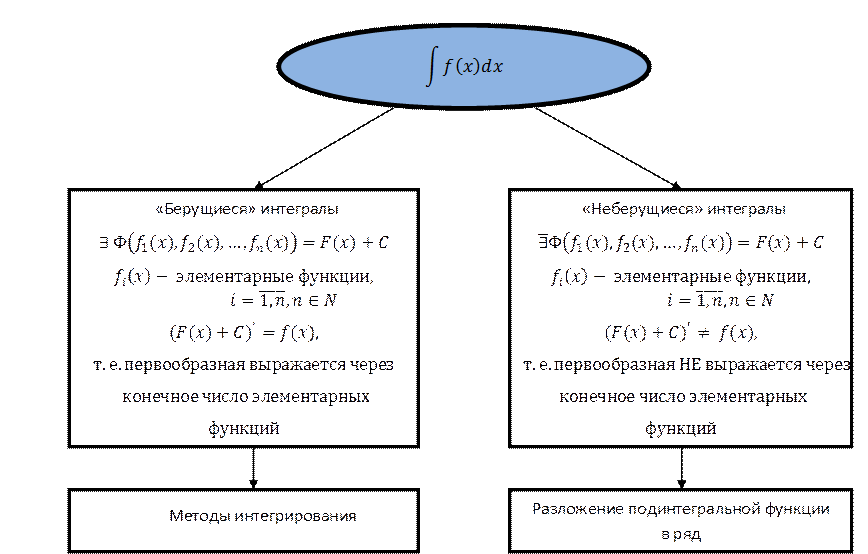
Примеры «неберущихся» интегралов
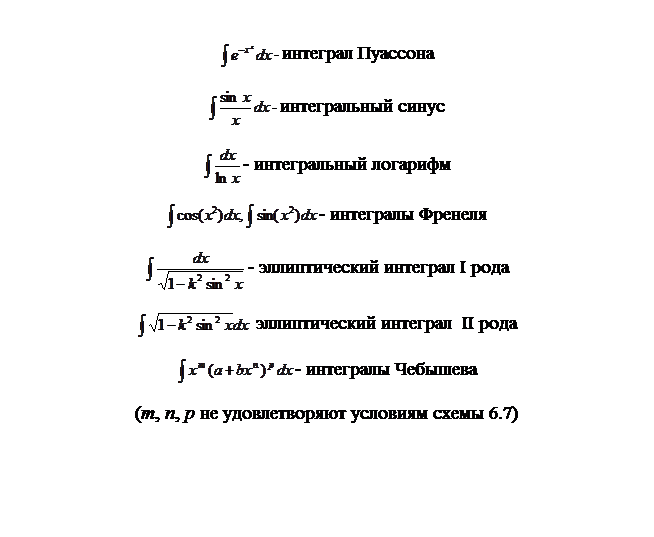
6.10.Итоговая таблица основных методов интегрирования
| Вид интеграла
| Метод интегрирования
| 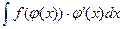
| Подстановка 
| 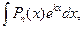


| Интегрирование по частям
 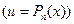
| 




| Интегрирование по частям
 
|  
 
| Двукратное интегрирования по частям
|
| Вид интеграла
| Метод интегрирования
|  (p2-4q<0) (p2-4q<0)
| Выделение полного квадрата
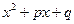 =(x + p/2)2+(q - p2/4)
и подстановка x + p/2=t =(x + p/2)2+(q - p2/4)
и подстановка x + p/2=t
|

| Выделяя в числителе дифференциал знаменателя, представляют интеграл в виде
суммы интегралов
 и и  , где u=x2 + px + q
или , где u=x2 + px + q
или
 ;
подстановка ;
подстановка 
| In= 
| Применение рекуррентной формулы
In= 
|
| Вид интеграла
| Метод интегрирования
|  (p2 - 4q <0)
(p2 - 4q <0)
| Выделяя в числителе дифференциал знаменателя, представляют интеграл в виде
суммы интегралов
 и и  , где u=x2 + px + q или , где u=x2 + px + q или
 ;
подстановка ;
подстановка 
| 
| Выделение целой части (если n  m), разложение знаменателя m), разложение знаменателя 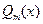 на множители
вида на множители
вида 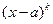 и и  и разложение рациональной дроби
и разложение рациональной дроби  на простейшие дроби
на простейшие дроби
| 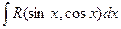
| Универсальная подстановка  , тогда
или частные подстановки: , тогда
или частные подстановки:
 1) если
1) если
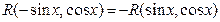 , то cosx = t;
2) если , то cosx = t;
2) если
 ,тоsinx = t;
3) если ,тоsinx = t;
3) если  , то tgx = t , то tgx = t
| 
| Универсальная или частные подстановки:
1) если m, n Î N и m, n – четные числа, то производится понижение степени формулами
 2) если m – нечетное положительное число, то
2) если m – нечетное положительное число, то
 применить подстановку сosx = t;
3) если n – нечетное положительное число, то используется подстановка sinx = t
применить подстановку сosx = t;
3) если n – нечетное положительное число, то используется подстановка sinx = t
| 
| Разложение подынтегральной функции по формулам:

| 
| Подстановка 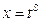 , где s – общий знаменатель дробей m1/n1, m2/n2, … , где s – общий знаменатель дробей m1/n1, m2/n2, …
| 
| Подстановка  , где s – общий знаменатель дробей m1/n1, m2/n2, … , где s – общий знаменатель дробей m1/n1, m2/n2, …
| 
| Выделение полного квадрата в подкоренном выражении и линейная подстановка
| 
| Выделяя в числителе производную подкоренного выражения, представляют интеграл в виде суммы интегралов
 и и  , где , где 
| 
| Подстановка  , приводящая
к интегралам вида , приводящая
к интегралам вида 
| 
| Рационализация с помощью одной из следующих подстановок:
 (или (или  ), ),
 (или (или  ), ),
 (или (или  ) )
| 
| Выделение полного квадрата в подкоренном выражении и линейная подстановка.
|  (m, n, p Є Q)
(m, n, p Є Q)
| Интегрирование заменой переменной:
1) если p Є Z, применяется подстановка x=tS , где s- общий знаменатель дробей m и n
2) если  , используется подстановка
a+bxn=tS, где s – знаменатель дроби p;
3) если , используется подстановка
a+bxn=tS, где s – знаменатель дроби p;
3) если  , применяется подстановка
ax-n+b=tS , где s – знаменатель дроби p , применяется подстановка
ax-n+b=tS , где s – знаменатель дроби p
|
Глава VII. Определенное и несобственное интегрирование. Элементы теории поля
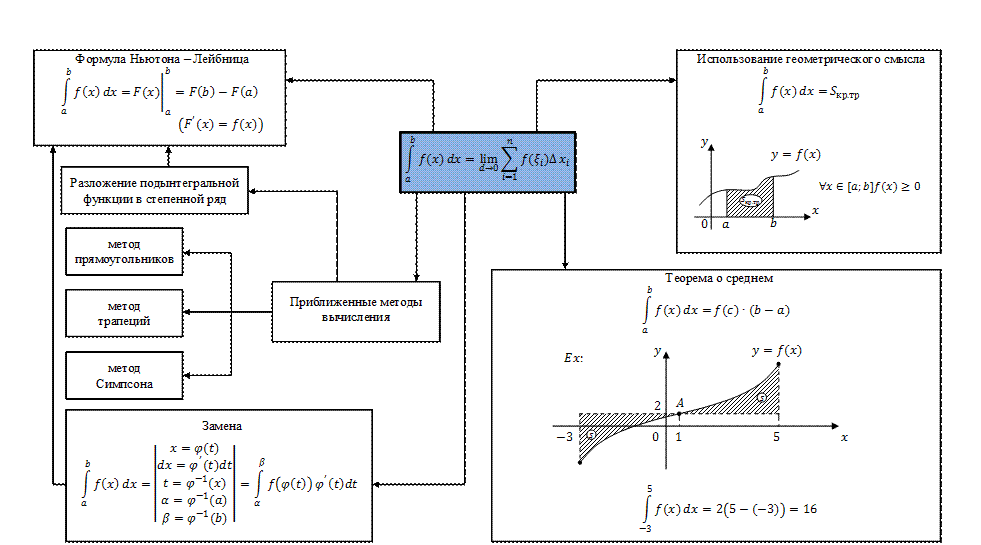
Вычисление определенного интеграла
7.2. Несобственные интегралы 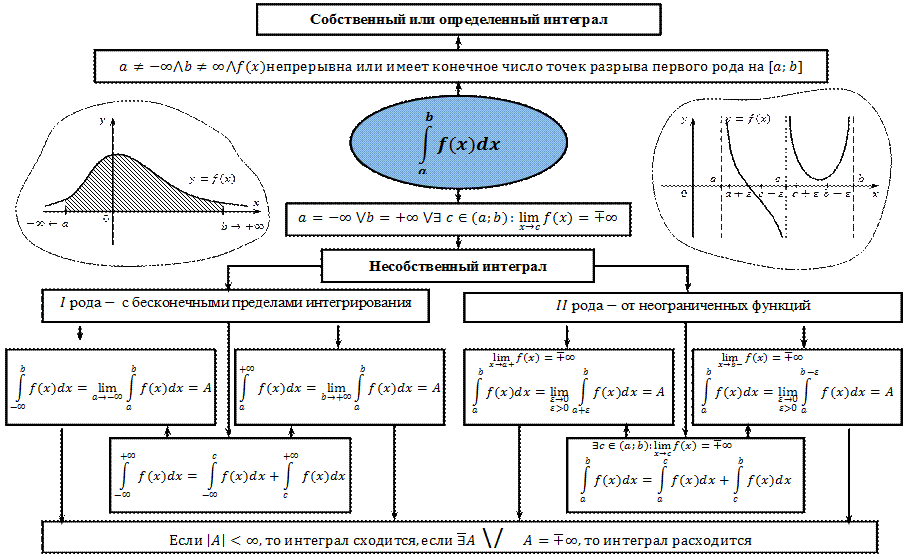
7.3. Криволинейные интегралы 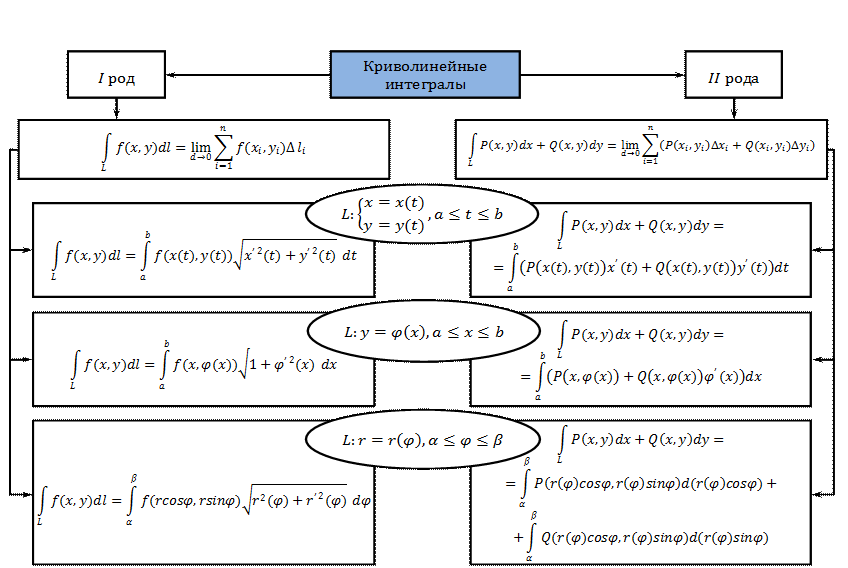
Технология вычисления двойного интеграла

Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|








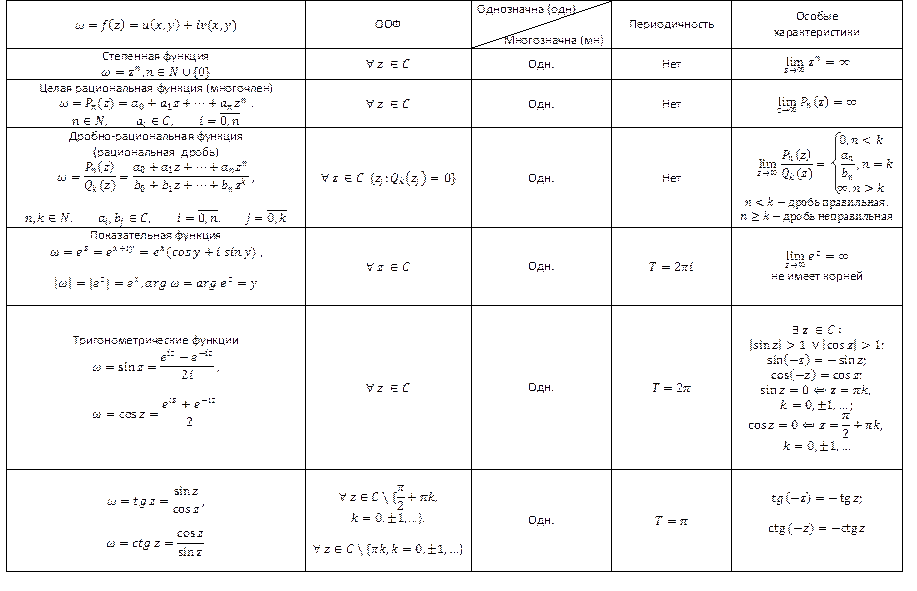
 ,
,
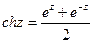


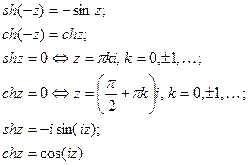
 ,
,


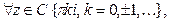

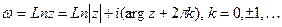


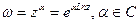
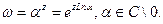
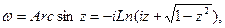

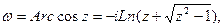
 Обратные гиперболические функции:
Обратные гиперболические функции: 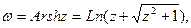




 5.5. Простейшие поверхности второго порядка
5.5. Простейшие поверхности второго порядка

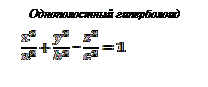






















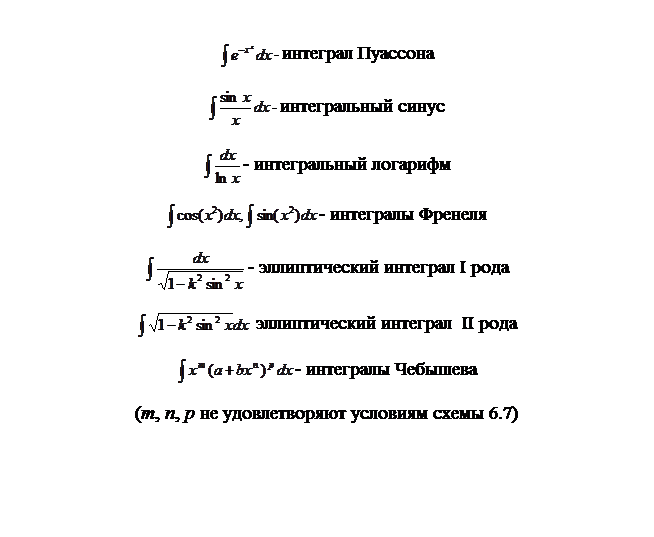
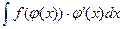

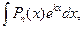



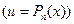










 (p2-4q<0)
(p2-4q<0)
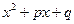 =(x + p/2)2+(q - p2/4)
и подстановка x + p/2=t
=(x + p/2)2+(q - p2/4)
и подстановка x + p/2=t

 , где u=x2 + px + q
или
, где u=x2 + px + q
или
 ;
подстановка
;
подстановка 


 (p2 - 4q <0)
(p2 - 4q <0)

 m), разложение знаменателя
m), разложение знаменателя 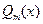 на множители
вида
на множители
вида 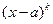 и
и  и разложение рациональной дроби
и разложение рациональной дроби  на простейшие дроби
на простейшие дроби
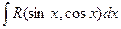
 , тогда
или частные подстановки:
, тогда
или частные подстановки:
 1) если
1) если
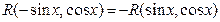 , то cosx = t;
2) если
, то cosx = t;
2) если
 ,тоsinx = t;
3) если
,тоsinx = t;
3) если  , то tgx = t
, то tgx = t

 2) если m – нечетное положительное число, то
2) если m – нечетное положительное число, то
 применить подстановку сosx = t;
3) если n – нечетное положительное число, то используется подстановка sinx = t
применить подстановку сosx = t;
3) если n – нечетное положительное число, то используется подстановка sinx = t



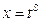 , где s – общий знаменатель дробей m1/n1, m2/n2, …
, где s – общий знаменатель дробей m1/n1, m2/n2, …

 , где s – общий знаменатель дробей m1/n1, m2/n2, …
, где s – общий знаменатель дробей m1/n1, m2/n2, …




 , приводящая
к интегралам вида
, приводящая
к интегралам вида 
 (или
(или  ),
),
 (или
(или  ),
),
 (или
(или  )
)

 (m, n, p Є Q)
(m, n, p Є Q)
 , используется подстановка
a+bxn=tS, где s – знаменатель дроби p;
3) если
, используется подстановка
a+bxn=tS, где s – знаменатель дроби p;
3) если  , применяется подстановка
ax-n+b=tS , где s – знаменатель дроби p
, применяется подстановка
ax-n+b=tS , где s – знаменатель дроби p



