
|
|
Сравнение двух линий регрессииИзложенный здесь материал следует читать после ознакомления с разделом 8. Регрессионный анализ, рассматривая зависимость между признаками, выражает ее специфическим образом – через уравнения регрессии. Линейные уравнения вида Y = ax+b содержат два коэффициента регрессии, характеризующие степень сопряжения и пропорциональность изменения признаков (коэффициент a отражает силу связи, т. е. наклон линии) и место пересечения оси ординат (коэффициент b определяет место положения линии в осях координат). Когда ставится вопрос о сходстве характера связи между признаками, то в отношении линии регрессии он распадается на три отдельных вопроса: – одинаков ли характер распределения признаков? – одинаков ли наклон линий регрессии? – одинаково ли положение линий регрессии относительно осей координат? 1) Для того чтобы решить вопрос о сходстве угла наклона линий регрессии, необходимо убедиться в том, что обе линии характеризуются одной и той же случайной дисперсией, сходным характером рассеяния вариант вокруг линий, т. е. сходными значениями случайной дисперсии, Но:
где 2) Если остаточные дисперсии для разных линий значимо не отличаются, можно приступать к сравнению коэффициентов регрессии, определяющих характер зависимости между признаками, т. е. ответственных за угол наклона прямых. Этой цели служит T критерий Стьюдента:
где a1, a2 – коэффициенты регрессии сравниваемых уравнений, ma1,2 – обобщенная ошибка коэффициентов регрессии. Для выборок одинакового объема обобщенная ошибка рассчитывается по формуле:
где ma1, ma2 – ошибки коэффициентов регрессии:
Sy, Sx – стандартные отклонения, рассчитанные по всему объему выборки n, r – коэффициент корреляции между признаками x и y. Для выборок, имеющих разный объем, обобщенная ошибка репрезентативности коэффициентов регрессии вычисляется более сложным путем:
где
Сx1, Cx2 – суммы квадратов отклонений значений признака x от своих средних (MX) в двух выборках:
Различие между коэффициентами регрессии a1 и a2 считается значимым, если расчетное значение критерия Стьюдента превосходит табличное значение при заданном уровне значимости и числе степеней свободы df = n1+n2–4.
3) Если критерий Стьюдента не показал отличий коэффициентов регрессии, то проверяется, наконец, третья гипотеза – об одинаковом положении линий регрессии (т. е. гипотеза о полном совпадении линий) – с помощью T критерия Стьюдента:
где a – усредненный коэффициент корреляции
Mx1, Mx2 – средние для признака x в двух выборках, Различие между коэффициентами регрессии b1 и b2 считается значимым, если расчетное значение критерия Стьюдента превосходит табличное значение при заданном уровне значимости и числе степеней свободы df = n1+n2–3. В качестве примера сравним характер зависимости между длиной хвоста (Lc, мм) и длиной тела (Lt, см) у самцов (m) и самок (f) обыкновенной гадюки (табл. 6.3), уравнения регрессии приведены на иллюстрации (рис. 6.2). 1) Найти остаточные дисперсии Получим отсюда Поскольку полученное значение (3.04) меньше табличного F(α,df1,df2) = 3.4, отличия между дисперсиями незначимы. Можно продолжать сравнение линий регрессии. 2) Для проверки различий коэффициентов регрессии требуется найти обобщенную ошибку ma1,2, используя значения ошибок из таблиц проведенного ранее регрессионного анализа в среде Excel. Поскольку объемы выборок отличаются не сильно, можно использовать первую формулу:
Таблица 6.3
Рис. 6.1. Регрессия длины хвоста по длине тела у гадюк Для целей иллюстрации рассчитаем и более точную оценку. Для этого предварительно нужно найти суммы квадратов отклонений значений независимой переменной x (в нашем случае ее роль играет длина тел Lt) от своих средних. Найдем величины с помощью функции Excel =КВАДРОТКЛ(диапазон). Для таблицы 6.3 имеем: Cx1 =КВАДРОТКЛ(C2:C9) = 62, Cx2 =КВАДРОТКЛ(C11:C19) = 52.222. Поскольку общая остаточная дисперсию
обобщенная ошибка коэффициентов регрессии составит:
т. е. практически не отличается от рассчитанной первым способом. Теперь можно оценить значимость отличий коэффициентов (для df = n1+n2–4 = 8+9–4 = 13):
Полученное значение критерия Стьюдента больше табличного даже для уровня значимости α = 0.001(T(0.001,13) = 4.22), т. е. коэффициенты регрессии не равны. Итак, результаты сравнения показывают, что линии регрессии имеют разный угол наклона; с увеличением размеров тела длина хвоста у самцов (a = 1.2) прирастает быстрее, чем у самок (a = 0.7). 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 . Эта первая гипотеза проверяется с помощью F критерия Фишера:
. Эта первая гипотеза проверяется с помощью F критерия Фишера: ~ F(α, df1, df2),
~ F(α, df1, df2),  ,
, – остаточная дисперсия, сумма квадратов отклонения исходных значений (yx) от рассчитанных по уравнению регрессии (Yx), нормированная на число степеней свободы (n–2). Это значение получают из таблицы дисперсионного анализа регрессионной модели ("Остаток").
– остаточная дисперсия, сумма квадратов отклонения исходных значений (yx) от рассчитанных по уравнению регрессии (Yx), нормированная на число степеней свободы (n–2). Это значение получают из таблицы дисперсионного анализа регрессионной модели ("Остаток"). ~ T(α, df),
~ T(α, df),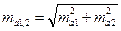 ,
, ,
, ,
, – обобщенная остаточная дисперсия, вычисленная по формуле:
– обобщенная остаточная дисперсия, вычисленная по формуле: ,
, ,
, – остаточные дисперсии (см. выше).
– остаточные дисперсии (см. выше). ~ T(α, df),
~ T(α, df), ,
,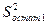 = 12.202,
= 12.202,  = 4.006,
= 4.006, = 3.046.
= 3.046.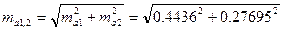 = 0.52298.
= 0.52298.

 2.7908,
2.7908, = 0.52419
= 0.52419 = 10.76.
= 10.76.