
|
|
Ошибка репрезентативности выборочных параметров
По части никогда не удается полностью охарактеризовать целое, всегда остается вероятность того, что оценка генеральной совокупности на основе выборочных данных недостаточно точна, имеет некоторую большую или меньшую ошибку. Такие ошибки, представляющие собой ошибки обобщения, экстраполяции, связанные с перенесением результатов, полученных при изучении выборки, на всю генеральную совокупность, называются ошибками репрезентативности (репрезентативность – степень соответствия выборочных показателей генеральным параметрам). Отличия значений выборочных параметров от генеральных называются ошибкой репрезентативности данного параметра, или просто (статистической) ошибкой. Проиллюстрируем это примером. Из лабораторной культуры взяли 8 выборок по 10 одновозрастных дафний. У каждой из них промеряли длину тела. По каждой группе получены следующие средние значения (M): M1 = 4.09, M2 = 3.85, M3 = 3.88, M4 = 3.94, M5 = 3.86, M6 = 3.89, M7 = 3.97, M8 = 3.90 мм. Общая средняя Mобщ. = 3.92 мм. Несмотря на то, что измерялись особи из одной культуры (одинаковые для всех генотипы и условия содержания), получены разные средние величины. Эти отличия и есть ошибки репрезентативности, связанные с неточностью оценок по небольшим выборкам. Если теперь мы найдем среднеквадратичное отклонение этих отдельных средних от общей, оно будет характеризовать средний диапазон отклонения выборочных оценок от генеральных значений. В данном случае показатель изменчивости средних составляет SM = 0.078513 ≈ 0.08 мм. Эта величина называется ошибкой средней арифметической (или стандартной ошибкой) и является по существу средним квадратичным отклонением множества выборочных средних от генеральной средней. На практике обычно нет возможности делать несколько выборок и вычислять несколько выборочных средних, чтобы по ним проводить расчеты. Статистическая теория показывает, что ошибка средней в Используя это уравнение, были рассчитаны ошибки для разных выборок нашего примера, которые принимали значения от 0.05 до 0.11 мм, что оказалось близко к точной величине ошибки SM =0.08. Статистические ошибки служат мерой тех пределов, в которых выборочные частные оценки могут отклоняться от параметров генеральной совокупности. Как следует из конструкции расчетной формулы, величина ошибки тем больше, чем больше варьирование признака (S) и чем меньше выборка (n). При увеличении объема выборки ошибки репрезентативности стремятся к нулю (следствие закона больших чисел). Ошибку репрезентативности имеют все статистические параметры, рассчитанные по выборке: средняя, стандартное отклонение, коэффициент вариации, показатели асимметрии и эксцесса. Для разных типов распределений расчетные формулы могут немного изменяться. Для нормального распределения они имеют следующий вид. Ошибка средней: ошибка стандартного отклонения: ошибка коэффициента вариации: Вычисленные значения ошибок подставляют к соответствующим параметрам со знаками плюс-минус (параметр ±ошибка) и в такой форме представляют в научных отчетах и публикациях. Вернемся к примеру с весом тела бурозубок и определим соответствующие ошибки средней арифметической: стандартного отклонения: коэффициента вариации: Используя понятие ошибки репрезентативности, можно показать, почему в формуле расчета выборочной оценки стандартного отклонения (см. стр. 43) используется число степеней свободы n–1 вместо объема выборки n. Выборочная дисперсия S² оценивает генеральную дисперсию σ² неточно и отличается от нее в среднем на величину ошибки m²S : σ² = S² – m²S. В то же время известно, что ошибка в n раз меньше выборочной дисперсии m²S = S²/n. Отсюда σ² = S² – S²/n = n∙S²/n – S²/n = S²∙(n–1)/n, σ² = S²∙(n–1)/n или σ²∙n = S²∙(n–1). Иными словами, выборочная дисперсия должна быть несколько больше, чем дает формула без учета ошибки, т. е. формула для ее расчета должна включать в знаменатель число степеней свободы n–1 вместо объема выборки n. Не следует путать статистическую ошибку с методическими ошибками и ошибками точности (точности измерений, анализов, подсчетов и т. д.), хотя методические погрешности и увеличивают ошибку репрезентативности, но другим путем – методические огрехи увеличивают изменчивость признака, стандартное отклонение. Чем лучше взята выборка, чем больше ее размеры, т. е. чем вернее отражает она генеральную совокупность (все явление, весь процесс в полном объеме), тем меньше статистическая ошибка и расхождение между значениями признаков в выборочной и генеральной совокупностях. При всей неизбежности статистической ошибки она может быть сведена к минимуму отбором достаточного числа особей (вариант). С ростом объема выборки оценки параметров стабилизируются, а их ошибки репрезентативности уменьшаются.
Доверительный интервал
При конкретных биологических наблюдениях параметры генеральной совокупности остаются неизвестными, о них судят по выборочным оценкам, используя для этого величину ошибок репрезентативности. Границы, в которых с той или иной вероятностью находится параметр генеральной совокупности, называются доверительными, а интервал, заключенный между этими границами, – доверительным интервалом. Теоретические исследования поведения выборочных средних (как случайных величин) показали, что они подчиняются нормальному закону, большинство из них (95%) находится поблизости от генеральной средней – в диапазоне Mген.±1.96∙m. Это обстоятельство позволяет делать обратное заключение – генеральная средняя находится в диапазоне Mвыбор.±1.96∙m, т. е. предсказывать ширину интервала, в котором находится генеральный параметр, давать интервальную оценку генеральному параметру. В соответствии с законом нормального распределения можно ожидать, что генеральный параметр (истинное значение) окажется в интервале от М–T∙m до М+T∙m, где m – ошибка средней арифметической, T – квантиль распределения Стьюдента (табл. 6П) при данном числе степеней свободы (df) и уровне значимости (обычно α = 0.05). Сказанное можно перефразировать так: с вероятностью P = 0.95 можно ожидать, что генеральная средняя находится в доверительном интервале М±T∙m, построенном вокруг выборочной средней арифметической M.
Возвращаясь к примеру о весе землероек-бурозубок, мы теперь можем записать доверительные интервалы при разных уровнях вероятности (граничные значения T взяты для случая n = ∞): Для Р = 0.95 М±T∙т = 9.3±1.96∙0.11 = 9.3±0.21 г; Для Р = 0.99 М±T∙т = 9.3±2.58∙0.11 = 9.3±0.28 г; Для Р = 0.999 М±T∙т = 9.3±3.30∙0.11 = 9.3±0.36 г. Таким образом, искомая генеральная средняя величина веса землероек с вероятностью P = 95% находится в пределах 9.11–9.53 г, с вероятностью P = 99% – 9.04-9.6, для P = 99.9% – 8.96–9.68 г. Если объем выборки, для которой были получены параметры и вычислялась ошибка репрезентативности m, был невелик (n<500), то необходимо вводить поправки на объем выборки, расширяя область возможного пребывания генерального параметра. Это понятно, поскольку при дефиците информации любые заключения не могут быть очень точными. Рассчитаем доверительный интервал для тех же данных, но с объемом n = 20 экз. Ошибка средней арифметической составит При уровне значимости α = 0.05 и числе степеней свободы df = n–1 = 20–1 = 19 табличная величина статистики Стьюдента равна T = 2.09, тогда доверительный интервал составит: М±T∙т = 9.3±2.09∙0.2 = 9.3±0.41 г – от 8.9 до 9.7 г. Аналогичным образом можно построить доверительный интервал для стандартного отклонения (S±TmS), коэффициента вариации(CV±TmCV), а также других статистических параметров (коэффициентов асимметрии, эксцесса, регрессии, корреляции), рассмотренных в следующих разделах.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 раз меньше, чем стандартное отклонение. Значит, ошибку можно рассчитать для единичной отдельной выборки по формуле:
раз меньше, чем стандартное отклонение. Значит, ошибку можно рассчитать для единичной отдельной выборки по формуле: (SM обозначается как m).
(SM обозначается как m). ,
, ,
,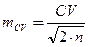 .
. , M = 9.3±0.11 г;
, M = 9.3±0.11 г; , S = 0.89±0.079 г;
, S = 0.89±0.079 г; , CV = 9.6±0.9 %.
, CV = 9.6±0.9 %.
 г, M = 9.3±0.2 г.
г, M = 9.3±0.2 г.