
|
|
Оптимальный объем выборки
В биологических исследованиях, при планировании экспериментов, для определении величины подопытных и контрольных групп часто заранее требуется установить число наблюдений, достаточное для получения правильного представления о явлении в целом (получить репрезентативные оценки генеральной совокупности). Можно говорить о двух разных подходах для непрерывных и дискретных признаков. Идея первого метода состоит в том, чтобы, используя известные соотношения (все формулы были представлены выше) между средней, стандартным отклонением, ошибкой средней, плотностью вероятности распределения Стьюдента (на их основе вычисляется коэффициент вариации, показатель точности оценок, доверительный интервал), найти число степеней свободы, соответствующее доверительному интервалу для средней при уровне значимости α = 0.05. Иными словами, решается задача, прямо противоположная рассмотренной в предыдущем разделе. Объем выборки, достаточной для получения результата заданной точности, находят по формуле:
где п – объем выборки, T – граничное значение из таблицы распределения Стьюдента (табл. 6П), соответствующее принятому уровню значимости при планируемом объеме выборки (в крайнем случае можно взять значение T = 1.96 для df = ∞), CV – приблизительное значение коэффициента вариации (%), ε – планируемая точность оценки (погрешности) (%). Рассчитаем необходимый объем условной выборки, обеспечивающий хорошую точность ε = 3%, для уровня значимости α = 0.05 (T = 1.98, для df ≈ 100) и для коэффициента вариации CV = 12% (такова относительная изменчивость многих размерно-весовых признаков животных):
Определим объем выборки, необходимый для определения среднего веса землероек-бурозубок при условии, что доверительный уровень вероятности должен составить 99% (α = 0.01), показатель точности оценки 3% при сохраняющемся уровне изменчивости CV = 10%. По таблице Стьюдента (табл. 6П) в соответствии с заданным уровнем значимости (α = 0.01) и для того же числа наблюдений находим T = 2.62. Далее вычисляем необходимый объем выборки:
Если исследуется фенотипическое (видовое) разнообразие, может возникнуть задача определения минимального объема выборки, в которой будет присутствовать хотя бы один экземпляр с определенным фенотипом (Животовский, 1991). С позиций теории вероятности задача ставиться так: определить объем выборки, в которой с вероятностью P можно ожидать присутствие особи с признаком, частота которого в генеральной совокупности составляет π. Предлагается следующая формула:
В первом приближении значение π можно определить приблизительно по имеющимся данным. Что же касается вероятности P, то ее уровень довольно сильно влияет на величину необходимого объема выборки. Для большей надежности следует брать P = 0.99, но тогда возрастет объем работ; не столь высокие требования (P = 0.95) могут и не позволить найти искомый фенотип. В частности, при уровне вероятности P = 0.95 и предположительной частоте фенотипа в популяции π = 0.05 потребуется
чтобы отловить хотя бы одну особь с этим дискретным признаком. Нетрудно рассчитать небольшую таблицу, содержащую оценки необходимых объемов выборок для разной вероятности отлова и различных частот фенотипов в популяции.
В случае исследования нескольких фенотипов существует достаточно сложный метод расчета объема выборки, в которой с вероятностью P присутствуют все фенотипы, частоты которых в популяции не меньше, чем πmin. Фрагмент такой таблицы может оказаться полезным для примерного определения нужных объемов выборок.
Асимметрия и эксцесс
В практике биологических исследований нередки случаи, когда числовые значения признаков дают распределения, в той или иной мере отличающиеся от нормального. Иногда обнаруживается асимметричное, в других сериях – эксцессивное распределение (рис. 3.1, 3.2). Для асимметричных вариационных кривых характерно появление "хвоста" – сдвиг частот от средних значений вправо или влево. В распределении эксцессивных признаков наблюдается чрезмерное накапливание или, наоборот, снижение частот в центральных классах вариационного ряда, вследствие этого вершина кривой распределения либо сильно поднимается и заостряется (положительный эксцесс, островершинность), либо, напротив, опускается, приобретая вид широкого плато (отрицательный эксцесс, туповершинность) или даже седловины между двумя боковыми вершинами. Для нормального распределения коэффициенты асимметрии и эксцесса равны нулю. При расчете коэффициентов асимметрии и эксцесса используются следующие базовые формулы:
Однако для ответственных случаев разработаны более сложные формулы, дающие несмещенные оценки:
Эти последние формулы реализованы в среде Excel в виде функций: для оценки асимметрии =СКОС(диапазон) и для оценки эксцесса =ЭКСЦЕСС(диапазон). Диапазон ячеек должен содержать все значения изучаемой выборки. Конфигурация кривых распределения отражает существенные биологические особенности изучаемых процессов и явлений, и потому заслуживает специальной оценки и анализа. Как показали исследования академика С. С. Шварца и его учеников, характер кривой распределения одного из жизненно важных признаков изучаемой популяции животных может указать на определенную тенденцию в действии и направлении естественного отбора.
Рис. 3.1. Асимметрия распределения (обозначена пунктиром относительно нормальной кривой): А – положительная (правосторонняя), Б – отрицательная (левосторонняя)
Если вариационные кривые, характеризующие изменчивость отдельных признаков, асимметричны, это может означать стремление отбора изменить среднюю норму изменчивости популяции путем преимущественной элиминации худших (в данных условиях) особей (ведущий отбор). Если же фиксируемое состояние популяции на данном этапе ее развития стабильно (поддерживается стабилизирующим отбором), то изменчивость отдельных признаков у особей данной популяции должна подчиняться закону нормального распределения: отклонения от средней в сторону плюс- и минус-вариант должны встречаться одинаково часто. Асимметричности в этом случае, естественно, не наблюдается.
Рис. 3.2. Эксцесс распределения (обозначен пунктиром относительно нормальной кривой): А – положительный (островершинность), Б – отрицательный (туповершинность) Не меньшую информативную нагрузку несет и характер эксцесса вариационной кривой. Ярко выраженный отрицательный эксцесс распределения однородного по возрастному и половому составу материала может свидетельствовать о действии на популяцию дизруптивного отбора и о тенденции изучаемого вида образовывать не только обычные, типичные формы, но и давать в повышенном количестве новые для него вариации, сильно уклоняющиеся от нормы. При сильном положительном эксцессе не исключено ужесточение стабилизирующего отбора. Показатели асимметрии и эксцесса используются в качестве тестов для проверки соответствия эмпирического распределения нормальному и биномиальному законам. Статистическая значимость этих показателей говорит о нарушении нормальной формы кривой распределения. Критерии Стьюдента для df = ∞ проверяют нулевую гипотезу Но: "коэффициент асимметрии (эксцесса) существенно от нуля не отличается, следовательно, асимметрия (эксцесс) достоверно не выражена":
где Точная и приближенная формулы для расчета статистической ошибки показателя асимметрии и эксцесса составляют:
Проведем вычисление коэффициентов асимметрии и эксцесса для данных по массе бурозубок: A =СКОС(A2:A64) = 0.608664019, mA = КОРЕНЬ(6* 63*( 63-1)/(( 63-2)*( 63+1)*( 63+3))) = 0.301588566, TA = 2.018193285, E =ЭКСЦЕСС(A2:A64) = 1.130099794, mE = КОРЕНЬ(24*C8*(C8-1)^2/((C8-3)*(C8-2)*(C8+3)*(C8+5))) = = 0.594840621, TE = 1.899836283.
Табличное значение критерия Стьюдента составляет T(0.05,∞) = 1.96. Поскольку полученное значение TA = 2.02 больше табличного (1.96), коэффициент асимметрии значимо отличается от нуля. По массе тела бурозубки распределены с правосторонней асимметрией, что понятно, поскольку в летних отловах большинство животных – разновозрастные молодые (с нормальным распределением), а меньшинство – зимовавшие (более тяжелые и скопившиеся справа). Поскольку полученное значение TE = 1.90 меньше табличного (1.96), коэффициент эксцесса значимо от нуля не отличается. Распределение в целом близко к нормальному, что подтверждает предыдущее объяснение асимметрии. Вычислить все рассмотренные параметры вариационного ряда можно в среде Excel с помощью макроса, который вызывается командой меню Сервис\ Анализ данных\ Описательная статистика. Например, обработка данных по массе бурозубок дает следующие результаты:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ,
, ≈ 63 экз.
≈ 63 экз. ≈ 75 экз.
≈ 75 экз.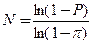 .
. = 58.4 ≈ 59 экз.,
= 58.4 ≈ 59 экз.,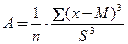 ,
, .
. ,
, .
.

 ,
,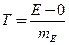 ,
, – статистическая ошибка соответствующего коэффициента.
– статистическая ошибка соответствующего коэффициента. ,
, .
.