
|
|
ГЕОМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ КОМПЛЕКСНОГО ЧИСЛАПринято комплексное число a + bi изображать точкой на плоскости. Абсцисса этой точки равна действительной части комплексного числа a, ордината равна b, коэффициенту при мнимой единице. Таким образом, всякому комплексному числу соответствует определенная точка на плоскости, и наоборот, всякой точке на плоскости соответствует определенное комплексное число. Точкам, лежащим на оси Ох, соответствует действительная часть комплексного числа,поэтому осьОхназывается действительной осью. Точкам, лежащим на оси Оу, соответствуют мнимые числа,поэтому осьОуназывается мнимой осью.
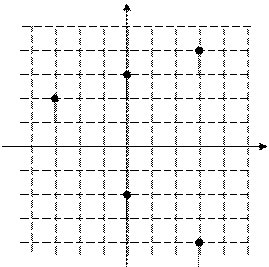
у Точке А соответствует число 3i Точке В соответствует число -3 + 2i М Точке С соответствует число -2i А Точке М соответствует число 3 + 4i Точке М1 соответствует число 3 - 4i В Точки М и М1 отличаются только знаком 0 1 2 3 4 хпередмнимой частью, этосопряженные числа. Пара сопряженных комплексных чисел симметрична относительно оси абсцисс. С
М1
Плоскость, на которой задается комплексное число, называется плоскостью комплексной переменной.Наряду с изображением комплексного числа точками на плоскости удобно с каждым комплексным числом связать вектор, исходящий из начала координат в точку, изображающую это число (т.е. радиус- вектор этой точки). Величина угла
В(х;у) Длина вектора у называется модулем этого числа и обознается |
0 х оси координат, и вычисляются согласно
формулам: x = r cos
ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ В АЛГЕБРАИЧЕСКОЙ ФОРМЕ Запись Z = a + bi называется алгебраической формой комплексного числа. Сложение (вычитание)комплексных чисел выполняется по формуле:
Z1 = a1 ± b1i Z2 = a2 ± b2iZ1 ± Z2 = a1 + b1i± (a2 + b2i) = (a1 ± a2) + i (b1i± b2) 3 + 2i- (5 + 7i) = 3 + 2i- 5 -7i= -(2 + 5 i)
Произведениекомплексных чисел выполняется по правилу умножения многочленов: Z = Z1· Z2 =(a1 + b1i) (a2 + b2i) = a1 a2 + a1 b2i+ a2 b1i + b1i b2i = a1 a2 - b1 b2 + i(a1 b2+ a2 b1 ) (2 - 3 i) (-5 + 4 i) = -10 + 8i+ 15i- 12 i2 = 2 + 23 i Делениекомплексных чисел определяется как действие, обратное умножению. Т.е. частнымдвух комплексных чисел Z1 и Z2 является такое комплексное число Z(a + bi) , которое, будучи умноженным на Z2, дает число Z1.
На практике частное двух комплексных чисел находят путем умножения числителя и знаменателя на число, сопряженное знаменателю (избавляются от «мнимости» в знаменателе.
Решить квадратные уравнения: 1. х2 + 2х + 5 = 0 х1,2 = 2. х2 - 6х + 18 = 0 х1,2 = 3. х2 - 4х + 5 = 0 х1,2 = 4. х2 - 10х + 41 = 0 х1,2 = Составить квадратные уравнения: в уравнении х2 + bх + с = 0 b = - (х1 +х2); с = х1 ·х2 1. х1 = с = х1 ·х2 = 1 + 3 = 4 уравнение х2 -2х + 4 = 0 2. х1 = с = х1 ·х2 = 8 + 1 = 10 уравнение х2 -6х + 10 = 0 3. х1 = с = х1 ·х2 =
Найти действительные числа х и у из условия равенства двух комплексных чисел
Два комплексных числа равны, если равны их действительные и мнимые части. Поэтому следует преобразовать обе части уравнения таким образом, чтобы 1.привести их к виду
b1i= b2i
1. 5х - 2у +(х + у)i = 4 + 5i
i(х + у) = 5i х + у = 5 2х + 2у = 10
7х = 14, х = 2 у = 3
2. 5хi - 2 + 4у = 9i + 2х + 3уi
i(5х - 3у) = 9i 5х - 3у = 9 5(2у -1) - 3у = 9 х = 3 3. 9 + 2хi + 4уi =10i + 5х - 6у
2х + 4у = 10 х + 2у = 5 3 х + 6у = 15 8х = 24, х = у = 1 4. 4х + 5у - 9 + 7(3х -у)i =10х + 14уi
5у -6х = 9 хi - iу = 0
Письменно ответьте на вопросы:
Выполните задания: 1. Выполните действия: а)
а) (1 + i)4 б)i + i 33 в)(1 - i)4 г)i 17 + i(1 - i)
2. Найдите действительные числа х и у из условия равенства двух комплексных чисел: а) 3 + 4хi + 5уi = 12i + 5х - 2у
б) х(2 + i) - у(1 - i ) = 1+ 3i в)х(1 + i) + у(2 + i ) = 3i + 1 3. Составьте квадратное уравнение по его корням:
х1 =

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
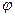 между положительным направлением действительной оси и вектором
между положительным направлением действительной оси и вектором 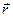 , изображающим число, является аргументом этого комплексного числа и обозначается arg
, изображающим число, является аргументом этого комплексного числа и обозначается arg 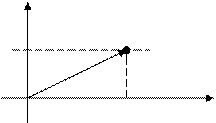 у
у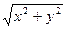
 = Z
= Z  Z1 =Z · Z2
Z1 =Z · Z2 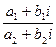 = Z(a + bi)
= Z(a + bi)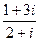 =
= 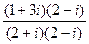 =
= 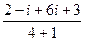 =
= 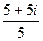 =1 + i
=1 + i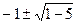 =
= 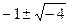 =
= 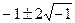 = - 1 ± i
= - 1 ± i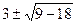 =
=  = 3 ± 3i
= 3 ± 3i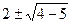 =
= 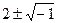 = 2 ± i
= 2 ± i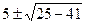 =
=  = 5 ± 4i
= 5 ± 4i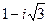 ; х2 =
; х2 = 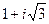 ;b = - (х1 +х2) = - (
;b = - (х1 +х2) = - ( 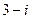 ; х2 =
; х2 = 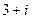 ;b = - (х1 +х2) = - (
;b = - (х1 +х2) = - ( 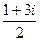 ; х2 =
; х2 =  ; b = - (х1 +х2) = - (
; b = - (х1 +х2) = - (  a1 + b1i= a2 + b2i, 2. решить систему уравнений a1 = a2
a1 + b1i= a2 + b2i, 2. решить систему уравнений a1 = a2

 4у - 2х = 2
4у - 2х = 2 
 3
3
 б)
б)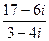 в)
в) г)
г)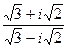
 (2 - 3i ) х2 =
(2 - 3i ) х2 =