
|
|
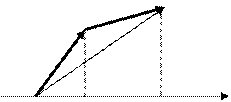
ДЕЙСТВИЯ С ВЕКТОРАМИ, ЗАДАННЫМИ СВОИМИ КООРДИНАТАМИРассмотрим принцип сложения векторов на примере плоской системы координат. 1. Найти координаты вектора
В
АхА хВ хС х
Легко заметить, что хС – хА = (хВ – хА) + ( хС – хВ) = прОх очевидно, уС – уА =( уВ – уА) + (уС – уВ ) = прОу Впространстве сложение производится по тем же правилам, что и в планиметрии, лишь дополнительно появляется третья координата. Пусть
Рассмотрим принцип умножения вектора на число на примере плоской системы координат. 2.Найти координаты вектора 3
О ОАх ОАх Bх
При умножении вектора, заданного своими координатами, на число его координаты умножаются на это число. Т.о. в координатной форме, если При этом:векторы п
Выполнить действия и ответ записать в координатной форме 1. Найти координаты векторов 2 2
2. Даны векторы
Найти координаты вектора
3. Координаты векторов Найти координаты вектора :
Если координаты векторов пропорциональны, то векторы коллинеарные. Т.е., если векторы
4Даны векторы Определяем координаты вектора
3т + 3п = -24
6т = -36, т = - 6 - 6п = 12, п = - 2
5. Даны точки А(2; -1; 0); В(-3; 2; 1) и С(1;1;1). Найти координаты точки D, если
D(11; -5; -1) 6. Даны точки А(-3;1; -1); В (2;-4; 1) , выразить через орты вектор
|
7Даны векторы
8. Даны точки А( 1;2; -1); В (-2; 1; 1) . Вычислить расстояние от начала координат до середины отрезка АВ С( |
Письменно ответьте на вопросы:
Выполните задания: 1. Даны точки А(-3; 1; -1) и В(2;-4; 1). Выразить через орты вектор 2. Вычислить координаты вектора 3. Даны точки А(1; 2; -1) и В(-2; 1; 1). Вычислить расстояние от начала координат до середины отрезка АВ. 4. Даны точки А(0; -1; 2) и В(- 1; 4; 1); С(- 2; 1; 0); D(-2; 1; 0). Вычислить координаты вектора т = 5. Выразить через орты вектор 6. Вычислить длину вектора
7. Вычислить длину вектора 8. На векторах
9. Доказать коллинеарность векторов 10. Выяснить, будут ли векторы
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
На основе введенных операций можно выражать одни векторы через другие. В частности, любой вектор можно представить в виде линейной комбинации ортов для координатных осей. На плоскости такое разложение вектора имеет вид Введенные операции сложения векторов и умножения вектора на число удовлетворяют всем требованиям, которые предусматриваются аксиомами линейного пространства. Однако структуру действий с векторами можно существенно обогатить, определив еще несколько операций, называемых произведением векторов. Первое из них называется «СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ». Термин «скалярное» означает, что в результате перемножения двух векторов
Рассмотрим несколько частных случаев:
1. Если вектор 2. Если хотя бы один из векторов - нулевой, то по определению 3. Скалярное произведение коммутативно: т.е. ( 4. Числовой множитель можно выносить за скобки: (
5. Если векторы
6. Если два вектора 7. В частности для ортов 8. Операция скалярного произведения векторов позволяет находить углы между ненулевыми векторами
1. Докажите, что векторы а) Два вектора перпендикулярны, если: х1х2 + у1у2 + z1z2 = 0, проверяем: 5·3 - 2·4 -7 = 0 б)
2. Определить, при каких значениях т, векторы будут взаимно перпендикулярны: а) Условие перпендикулярности векторов:х1х2 + у1у2 = 0 б) Условие перпендикулярности векторов:х1х2 + у1у2 = 0
3. Угол между векторами
|
4. Найти угол меду вектором т { 1; 0; 5. Найти угол между вектором т { 1; 0; Выберем произвольную точку на оси аппликат А(0;0;1), тогда вектор п { 0;0;1} сos
6. Найти углы меду векторами: а) сos б)
сos
в)
7. Определить угол А треугольника АВС, если А(1;3); В(4;6); С(3;1).
А(1;3) С(3;1) сos
8. Вычислить скалярное произведение векторов. а)
( 3
б) А(1;3); В(2;0); С(3;-4), вычислить произведение векторов

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
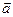 , если
, если 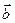 +
+ 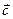
 С
С 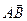 { (хВ – хА); (уВ – уА);( z В – zА) }
{ (хВ – хА); (уВ – уА);( z В – zА) }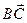 { (хС – хВ); (уС – уВ); ( z С – zВ) }
{ (хС – хВ); (уС – уВ); ( z С – zВ) }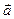 = ах
= ах 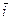 + ау
+ ау 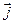 +аz
+аz 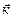 и
и 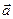 +
+ 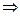







 х
х =
=  +
+ 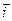 + y
+ y 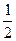
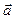 {-2; 0; 3 }
{-2; 0; 3 }  значит,
значит,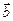 { 3;-1; -2} . Найти значения т и п, при которых векторы
{ 3;-1; -2} . Найти значения т и п, при которых векторы 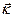 =
= 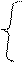 векторы коллинеарные
векторы коллинеарные 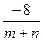 =
= 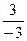 =
= 

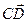 = -2
= -2 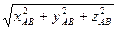 =
= 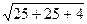 =
=  =3
=3 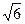
 ;
; 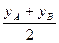 ;
; 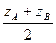 )
) | =
| =  =
= 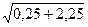 =
= 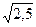

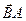 +
+  =
= 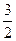
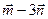 ) - (
) - ( 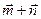 ), если
), если  = (2;3;1);
= (2;3;1); 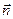 = (0; 1; 1).
= (0; 1; 1).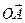 и
и  построен параллелограмм. Выразить в ортах его диагонали, если
построен параллелограмм. Выразить в ортах его диагонали, если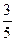 ; -
; -  };
};  ;
;  ; -
; - 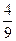 };
};  Скалярным произведениемдвух ненулевых векторов
Скалярным произведениемдвух ненулевых векторов 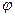 .
. Где
Где 
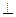
 ·
· 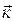 = 0; и т.д.
= 0; и т.д.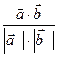 .
.
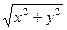 =
= 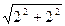 =
= 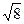
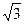 } и
} и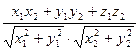 =
= 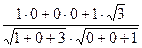 =
= 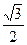
 =
= 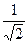
 =
= 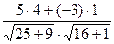 =
= 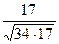 =
= 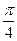
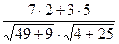 =
=  =
=  В(4;6)
В(4;6)  = 2
= 2 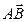 = 3
= 3 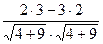 =
= 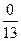 = 0
= 0 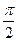
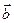 {2; 1 }, вычислить произведение векторов 3
{2; 1 }, вычислить произведение векторов 3 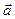 –
–