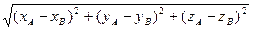|
|
ПОНЯТИЕ О СИСТЕМАХ КООРДИНАТIV. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
Положение материальной точки приходится определять в самых разных отраслях знаний, начиная от простейших земных механизмов, и до положения звезд в солнечной системе. Но положение точки может быть определено только по отношению к каким-то телам отсчета. С телом отсчета неподвижно связывают некоторую систему координат и только тогда определяют положение точки в этой системе координат. Таким образом, координатами вообщеназывают числа, определяющие положение точки в любой Момент времени. Что касается системы координат, то ее выбор диктуется соображениями удобства и простоты фиксации точки положения во времени или описания ее движения точки. Известны, например, координатная прямая, прямоугольные координаты на плоскости и в пространстве, географические координаты - параллели и меридианы на сферической поверхности; экваториальные координаты на небесной сфере - склонение и прямое восхождение. Самые употребительные координаты - прямоугольные. Введение такой системы координат позволяет приписать любой точке пространства определенный «адрес» в виде двух (в двухмерном случае) или трех (в трехмерном случае) чисел. I. Положение точки на плоскости определяется с помощью прямоугольной системы координат состоящей из пары взаимно перпендикулярных координатных прямых с общим началом координат. Начало координат обозначается буквой О, а координатные прямые обозначаются Ох и Оу и называются соответственно осью абсцисс и осью ординат. Единицы масштаба на обеих осях координатназываютсяединичными векторами,или ортами.Единичный вектор оси Ох обозначается Впервые прямоугольную систему координат ввел Рене Декарт (1596-1650). Поэтому прямоугольную систему координат называют также декартовой прямоугольной системой координат, а сами координаты - декартовыми координатами.Введениепрямоугольных координат на плоскости и в пространстве позволило свести многие геометрические задачи к чисто алгебраическим и, наоборот. Координаты х и у полностью определяют положение точки М на плоскости, т.к. каждой паре чисел х и у соответствует единственная точка М плоскости, и наоборот.
II четвертьI четверть N(х2;у2)
у1 - у2х1, у1, – это координаты проекций точки М
(С) отрезка МN на оси координат является число,
х1 - х2 пр.Ох МN = х М – хN=МN cos IIIчетвертьIVчетверть пр.Оу МN = уM - уN = МN sin
ВI четверти обе координаты точки имеют знак «+», в IIIчетверти обе координаты точки имеют знак «-», во II четверти координата у точки имеет знак «+», а координата х имеет знак «- », вIVчетверти координата х имеет знак «+», а координата у имеет знак «- ». Координаты середины отрезка определяются по формулам: хс =
Расстояние между двумя точками М иN на плоскости определяется формулой согласно теореме Пифагора для треугольника МNС: МN 2 = прОх МN 2 + прОу МN 2
II. Другой практически важной системой координат является полярная система координат.Полярная система координат задается точкой О, называемой полюсом; лучом Ор, называемым полярной осью, и единичным вектором Положение точки М однозначно определяется двумя числами: ее расстоянием r от полюса 0 и углом М(r;
r
0 [
Полярный угол ограничивают промежутком ( 0
Связь полярных координат с декартовыми координатами очевидна: у
А уА =rsin 0 хА = rcos
И она аналогична связи между коодинатами точки и ее проекциями в прямоугольной системе координат.
III. Положение точки в пространствеопределяется уже тремя координатами. Поэтому пространственная система координат состоит из трех взаимно перпендикулярных осей, пересекающихся в одной точке. Третья ось называется ось аппликат и обозначается ось Оz.Орты трех осей координат обозначаются соответственно:
z 1 О
У х Наибольшее распространение на практике получила правая система. Каждая пара координатных осей определяет координатную плоскость, а в совокупности они разбивают все пространство на 8 октантов.
осями Оу и Оz
zМ М(х;у;z) плоскость Oxy образуется в пространстве осями Ох и Оу 0 уМ у ось ординат хМ М(х;у;0) х ось абсцисс Каждой тройке чисел х, у, z сопоставляется одна и только одна точка пространства. И наоборот, каждой точке пространства
пространстве осями Ох и Оz
Если точка лежит накоординатной плоскости,то одна из ее координат равна 0:
F(0;y;z)
E(x;y;0) точки нет, поэтому, если мы хотим показать, что рассматриваем точку в трехмерном пространстве, то третью координату записывают равной нулю: E(x;y;0); у точки лежащей на плоскости Oуz,нулю равна координата x: F(0;y;z). У точки, лежащей в плоскости Oxz, нулю равна координата у: D(x;0;z). У точки, лежащей на оси координат, две из ее координат равны 0: Любую точку пространства можно рассматривать как вершину прямоугольного параллелепипеда, построенного на его осях координат. Тогда координаты этой точки(проекции точки на оси координат) x; y и z можно рассматривать как измерения прямоугольного параллелепипеда: a, b и c.
проекция
на плоскость YA Oxz XA х A1(x;y;o) – проекция точки А на плоскость Oyx
Пусть точка А -вершина параллелепипеда, тогда отрезок АО является его диагональю, и его длина вычисляется по известной формуле: d2 = a2 + b2 + c2, где a, b и c – измерения параллелепипеда, и одновременно координаты точки А(х, у, z), т.е. r(АО) = Случай, когда один конец отрезка совпадает с началом координат, весьма редкий и его можно рассматривать как частный случай. В общем виде концы отрезка с началом координат несовпадают. Тогда проекцией произвольного отрезка на ось координат является число, равное разности соответствующих координат проекций на эту ось концов данного отрезка. В пространстве это три отрезка xB - xA ; yB- уA и zB- zA
zB
0 хА х В х zA
х В – хАA yA yB y xA xB x Тогда расстояние между двумя точками, заданными своими координатами, равно корню квадратному из суммы квадратов разностей одноименных координат заданных точек

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
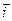 , единичный вектор Оу обозначается.
, единичный вектор Оу обозначается. 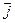 . Единицы масштаба на обеих осях координат берут, как правило, равными.
. Единицы масштаба на обеих осях координат берут, как правило, равными.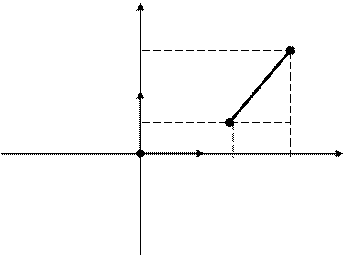 у
у
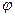 на оси координат, поэтому проекцией
на оси координат, поэтому проекцией 0 х данного отрезка на оси координат.
0 х данного отрезка на оси координат.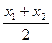 ус =
ус = 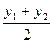 .
.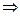 МN =
МN = 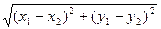
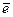 того же направления, что и луч Ор.
того же направления, что и луч Ор. r - полярный радиус,
r - полярный радиус, 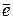
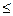
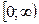 . В этом случае каждой точке плоскости (кроме 0) соответствует единственная пара чисел r и
. В этом случае каждой точке плоскости (кроме 0) соответствует единственная пара чисел r и 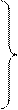
 r2 = х2 + у2
r2 = х2 + у2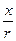
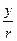 tg
tg 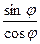 =
= 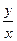
 . Существуют две различные конфигурации трехмерной системы координат: левая и правая
. Существуют две различные конфигурации трехмерной системы координат: левая и правая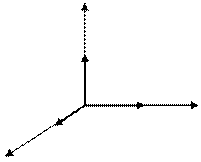
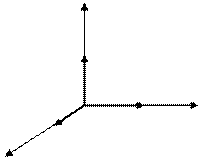 левая правая z
левая правая z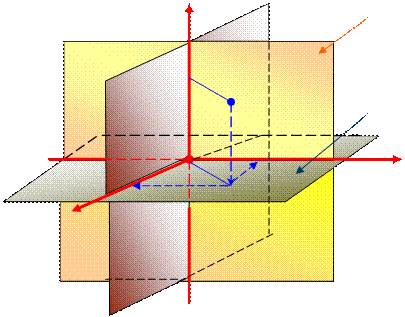 ось аппликатz плоскость Oуzобразуется в пространстве
ось аппликатz плоскость Oуzобразуется в пространстве  плоскость
плоскость  Z
Z

 ZF
ZF С(0;0;z)
С(0;0;z)  ZD
ZD
 D(x;0;z)
D(x;0;z)  0 (0;0;0) YF YE B(0;y;0) Если точка лежит в плоскости Oxy
0 (0;0;0) YF YE B(0;y;0) Если точка лежит в плоскости Oxy

 y (хорошо известной прямоугольной системе
y (хорошо известной прямоугольной системе X D A(x;0;0) координат), то у нее существуют две
X D A(x;0;0) координат), то у нее существуют две
 XE координаты x и y. Третьей координаты zу
XE координаты x и y. Третьей координаты zу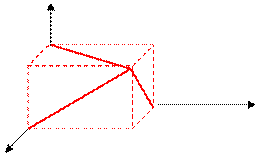 z
z А3(x;0;z0) ZA A2(0;y;z) - проекция точки А на плоскость Oyz.
А3(x;0;z0) ZA A2(0;y;z) - проекция точки А на плоскость Oyz.
 точки А A(x;y;z)
точки А A(x;y;z)
 0 у
0 у .
.
 уz
уz
 уВ В
уВ В уА А
уА А B
B