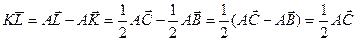|
|
Нулевой вектор коллинеарен любому вектору.Равными называются два сонаправленных вектора, имеющих равные модули. Равные векторы также называют свободными. Два вектора, равные третьему вектору, равны. Вектор можно перемещать вдоль прямой, совпадающей с его направлением и переносить его параллельно самому себе в любую точку пространства.
A В |
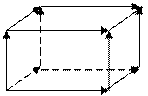
В параллелепипеде АВСDА1В1С1 D1 изобразить векторы: сонаправленные, противоположно направленные, равные. три группы коллинеарных,сонаправленных
А1 В1
D C А В D1 C1 Векторы коллинеарны А1 В1 D С
Компланарными называются три вектора, если при откладывании их от одной точки они лежат в одной плоскости. Любые два вектора - компланарные. Три вектора, два из которых коллинеарные, - компланарные.
В1 С1 Векторы
А1 D1
В С
А D
КООРДИНАТЫ ВЕКТОРА Координаты точки – это числа, соответствующиеее проекциям на оси координат. Проекциями произвольного отрезка на оси координат являются проекции этого отрезка на оси координат. Для вектора координатами вектора. Записывается:
При выполнении действий с векторами единицы масштаба
абсцисс, проекция вектора
уА А (3;2) И по правилу сложения векторов Такая запись называется: «Разложение вектора по ортам»
0 Если начало вектора не совпадает с началом координат, то координатами вектора являются его проекции на оси координат: (хВ– хА , уВ– уА). И тогда в координатной форме вектор у
уВ В (4;5) В прямоугольном треугольнике АСВ: катеты АС и ВС, гипотенуза - вектор
уА А(1;3) С заданы координаты точек А и В; или | векторзадан в координатной форме или в виде 0 хА х
пр.Оz
пр.Оу Х На плоскости пр.Ох х
Для трехмерного пространства во всех формулах добавляется третья координата:
|
Проекция вектора на ось равна произведению модуля вектора на косинус угла между вектором и осью: пр.Ох
Проекция вектора на ось отрицательное число (–),если вектор и ось имеют противоположные направления. или если
1.Проекции равных векторов на одну и ту же ось равны. 2. В данной системе координат каждый вектор имеет единственный набор координат. 3. Координаты вектора, отложенного от произвольной точки, равны разности 4.Векторы параллельны (коллинеарные) тогда и только тогда, когда их координаты
Графически это означает: 3 А (4;5; 3)
0 5 4 х А1(4;5) 2. Записать координаты векторов:
3. Если вектор отложен от начала координат, то координаты вектора равны координатам конца вектора. Векторы Упрямоугольного параллелепипеда ОА = 2, ОС = 3, ОО1 = 2. Найдите координаты векторов
O1 А1 (2; 0; 2)
2
С1(0,3;2); О1(0,0;2); А(2,0;0); С(0,3;0); В( 2; 3; 0)
4.Найти длину радиус- векторов | | | 5.Даны две координаты вектора
|
6. Какие координаты имеет вектор А(-5;4;-1):
7. Назовите координаты векторов: а) б)
8. Разложите по координатным векторам
8. Даны точки А(2; –3: 0); В(7; –12; 18); С (–8; 0; 5). Записать координаты векторов
Письменно ответьте на вопросы
Выполните задания: 1.Даны векторы 2. Запишите в координатной форме ВС, если С(-2; 1; 3); В(3; -2; 1) 3. Вершины куба имеют координаты А(3;-1;1); В(-1;-1;1); С(-1; 3; 1); С1 (-1; 3; 5). а) найдите координаты вершин В1 и D1 б) разложите по координатным векторам векторы:
4. Векторы
5. Определить, при каких значениях т векторы
6. Найдите значения т и п, при которых векторы
7. Векторы 8.Даны точки А(2; –3: 0); В(7; –12; 18); С (–8; 0; 5). Записать координаты векторов
9. Найти координаты вершины D параллелограмма АВСD, если А(3; 0; 1); В(4; 2; –1); С (1; 2; 5); 10. Проверить, являются ли точки А(– 4; – 4); В(–3; 4); С (4; 5); D(10; –2) вершинами трапеции АВСD.
СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ. УМНОЖЕНИЕ ВЕКТОРА НА Векторная алгебра - раздел математики, изучающий векторы. Векторная алгебра является одним из основных средств исследования в физике и разных разделах математики. В векторной форме записываются многие законы физики и механики, И в геометрии аппарат векторов позволяет кратко записывать формулировки задач и их решения, например, теорема о средней линии треугольника в векторной форме записывается так
К L
В С
Чтобы объединить преимущества координатного и векторного методов, для векторов введены координаты. Это позволяет свести действия с векторами к аналогичным действиям с их координатами, и проводить действия с векторами так, как это делается в обычной алгебре: слагаемые менять местами, вводить скобки, группировать, выносить за скобки как скалярные, так и векторные множители.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

 D С
D С
 ↑↑
↑↑  |
| 
 D1 C1 векторов:
D1 C1 векторов: 
 . . .
. . .  - равные векторы
- равные векторы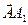

 ;
; 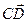
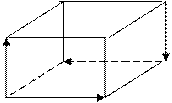 е, противоположно направленные
е, противоположно направленные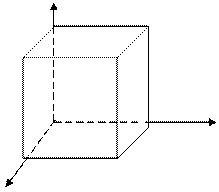
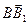
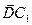 компланарные
компланарные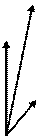
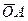 , имеющего начало в точке О(0;0), координаты точки А являются
, имеющего начало в точке О(0;0), координаты точки А являются 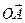 { хА; уА }. Такая запись называется: «Запись вектора в координатной форме». Пусть А(3;2), тогда
{ хА; уА }. Такая запись называется: «Запись вектора в координатной форме». Пусть А(3;2), тогда  у называют координатными векторами(ортами) и обозначают:
у называют координатными векторами(ортами) и обозначают: 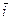 по оси
по оси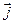 и по оси ординат и
и по оси ординат и 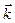 по оси аппликат.
по оси аппликат.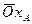 = 3
= 3 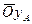 =2
=2 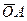 = х
= х 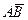 записывается:
записывается: 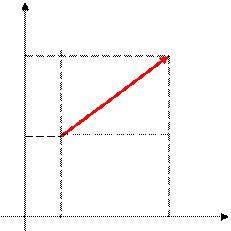
 у
у  |
|  , (1)если
, (1)если , (2)если
, (2)если Если
Если  0х, то проекции точек А и В совпадают и проекция вектора
0х, то проекции точек А и В совпадают и проекция вектора  у z Для трехмерного пространства
у z Для трехмерного пространства
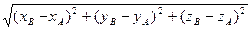 .
.


 <
< 
 1.Записать координаты вектора:
1.Записать координаты вектора: 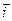 + 5
+ 5 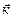 z
z 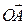
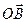 = – 4
= – 4 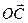 = – 2
= – 2 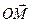 =
=  =
= 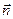 = 0,7
= 0,7  1;
1; 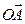 1 ;
1 ;  ;
; 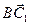 ;
; 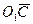 ;
; z
z




 С1
С1
 A1 В1
A1 В1
 O 3 С В1 ( 2; 3; 2)
O 3 С В1 ( 2; 3; 2)  2 у
2 у х A BО1( 0; 0; 2)
х A BО1( 0; 0; 2) 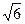 ); С(3; -2; 2
); С(3; -2; 2 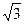 ).
).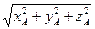 =
=  =
= 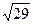
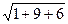 =
= 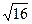 = 4
= 4 =
= 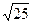 = 5
= 5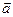 {4; -12; z} . Найти его третью координату, если:|
{4; -12; z} . Найти его третью координату, если:| 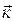
 =– 2
=– 2 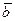 =
= 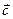 = – 3
= – 3 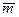 = – 5
= – 5  , если А(0;0;2) и С(0;2;0)
, если А(0;0;2) и С(0;2;0)
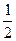 ; 0,75; –2
; 0,75; –2  } . Запишите координаты точек А(2; –3: 0); В(7; –12; 18); С (–8; 0; 5).
} . Запишите координаты точек А(2; –3: 0); В(7; –12; 18); С (–8; 0; 5).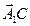 и
и 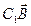
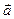 и
и 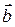 равны, если
равны, если  А
А 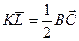 , а доказывается в одну строку:
, а доказывается в одну строку: