
|
|
ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ
Линейными операциями над векторами называют операции сложения, вычитания и умножения вектора на число. Действия с коллинеарными векторами В графической форме: если векторы Полученный результат не зависит от выбора точки А.
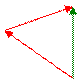
Действия с неколлинеарными векторами В графической форме действия с неколлинеарными векторамивыполняются поправилам треугольника ипараллелограмма, а в пространстве по правилупараллелепипеда. При сложении двух векторов оба слагаемых и результирующий вектор лежат в одной плоскости (почему?).
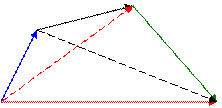
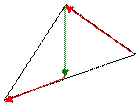
Если два вектора являются сторонами параллелограмма, то одна из диагоналей этого параллелограмма представляет сумму этих векторов, а вторая – разность.
В С В -
А D
Или по правилу треугольника: Пусть материальная точка А переместилась сначала в точку В, а затем в точку С. В результате двух перемещений, которые можно представить векторами С Т.е.
А В
Операция сложения векторов определяется следующим образом: чтобы сложить два вектора, необходимо от конца первого вектора отложить второй вектор и начало первого вектора соединить с концом второго.
Для операции сложения векторов справедливы свойства, аналогичные свойствам сложения чисел: 1.Переместительный закон:
2.Сочетательный закон:
В
А D Сложение нескольких векторов производится следующим образом: –от некоторой удобной точки откладывается первый вектор, от конца первого вектора откладывается второй и т.д. –начало первого вектора соединяется с концом второго, и этот вектор является суммой всех слагаемых векторов.
А В
–
–
А
в)
–
3. В треугольнике АВС укажите векторы:а) К С М а)
в) А В 4. В параллелограмме АВСD О - точка пересечения диагоналей АС и ВD. Найти
О О
А В 5.Втреугольнике АВСАD - медиана. Найти А
С D В
6.На стороне СD квадрата АBСD лежит точка Р так, что СР = РD, О –точка пересечения диагоналей. Выразите векторы
А D
7. На стороне BС ромба АBСD лежит точка K так, что ВК = КС, О –точка пересечения диагоналей. Выразите векторы B К С
О А 8. В параллелограмме АВСD О - точка пересечения диагоналей АС и ВD. АК = КО. Выразить
то одна из диагоналей этого параллелограмма О представляет сумму этих векторов К а вторая – разность: А В Некомпланарными являются три вектора, не лежащие в одной плоскости
в одной плоскости.
точки D, М, N не лежат в одной плоскости.
О
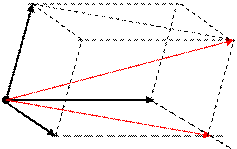
В Для сложения трех некомпланарных векторов пользуются правилом параллелепипеда– пространственным аналогом правила параллелограмма. Пусть векторы одной точкиО, т.е. их также можно сложить, пользуясь правилом параллелограмма.
1.В кубе ABCDA1B1C1D1 D1 C1 Выразить векторы
D С N S S A 2.В правильной треугольной призме ABC все ребра равны 1. A1К = КС1. Найти
т.к. тр-к A1 B1C1 - правильный и B1 К - высота в нем К C1 A B C 3.В пирамиде АBCDМ основание - параллелограмм,
А через
B D C М
4. ABCDA1 B1C1D1 - куб. AD =
К B1 A1 М D C
A B
Письменно ответьте на вопросы: 1. Сформулируйте правило параллелограмма, треугольника. Параллелепипеда 2. Как изображается противоположный вектор? 3. Какой векторный смысл имеют диагонали параллелограмма? 4. Когда два направленных отрезка изображают один и тот же вектор? Выполните задания: 1. Что можно сказать о векторах 2. Докажите, что в правильном пятиугольнике АBCDЕF сумма пяти векторов с началом в центре
3.В прямоугольном параллелепипеде ABCDA1B1C1D1 показать вектор, равный 4. Дан параллелограмм АВСD, точки Е и F лежат на сторонах АD и ВС. АЕ = ЕD, ВF :FС = 4 : 3. 5. ABCDA1B1C1D1 - прямоугольный параллелепипед. Найти 6. В прямоугольном параллелепипеде показать векторы:
7.В параллелепипеде ABCDA1 B1C1D1 разложить: вектор 8. В тетраэдре ABCD точки K и L - середины ребер AB и CD. Определить
9. В правильной треугольной призме ABСА1В1С1 сторона основания равна 1, точка Е - середина А1С1. Найдите |
10 Точка К не лежит в плоскости треугольника ABC. Е и Р - середины отрезков AB и ВС. Выразите вектор

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
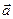 ,
, 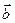 и
и 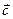 отложить последовательно от некоторой точки А , то суммой векторов
отложить последовательно от некоторой точки А , то суммой векторов 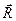 , начало которого совпадает с точкой А, аконец совпадает с концом вектора
, начало которого совпадает с точкой А, аконец совпадает с концом вектора 








 А
А


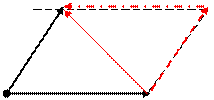

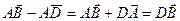
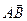 и
и 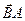 точка А переместилась из точки А в точку С.
точка А переместилась из точки А в точку С. =
= 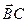
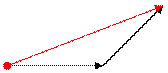


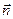
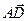 =
= 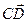 = (
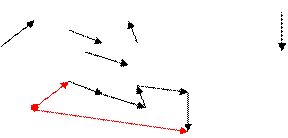
= (  =
= 

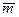
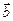
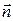
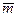 АВ =
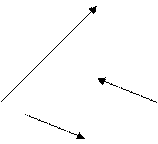
АВ =  Разностью векторов
Разностью векторов 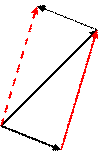
 Произведение вектора
Произведение вектора  (число) называется вектор
(число) называется вектор 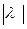 ·
· 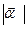 , коллинеарен вектору
, коллинеарен вектору 

 1. Если дан вектор
1. Если дан вектор  2. Для данных векторов
2. Для данных векторов 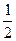
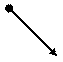
 В А
В А а);
а); 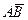 =
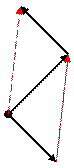
= 
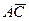 +
+ 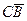 ; б)
; б)  б)
б) 
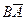 +
+ 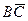 =
= 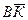
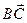 +
+ 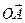
 D С
D С 
 С
С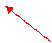
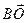 В
В -
- 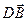

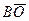 ,
,  ,
, 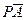 через векторы
через векторы 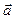 =
= 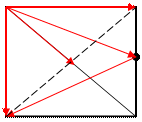 B С
B С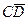 =
= 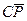 =
=  =
= 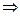
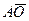 ,
, 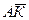 ,
,  через векторы
через векторы  .
.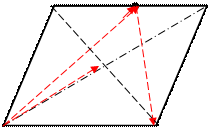 АBСD –ромб
АBСD –ромб 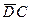 =
= 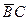 =
= 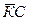 =
=  через
через 
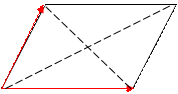 D С Если два вектора являются сторонами параллелограмма,
D С Если два вектора являются сторонами параллелограмма,
 (
(  D Векторы
D Векторы  ,
,  . Но векторы
. Но векторы 


 =
= 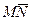 и
и 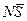
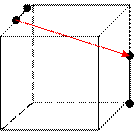
 М B1 N
М B1 N A1 D1 C1
A1 D1 C1
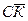 -
- 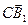

 A1 B1
A1 B1 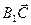 +
+  =
= 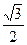
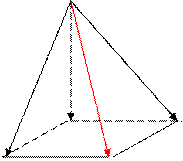 +
+ 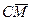 , но:
, но: 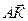 и
и  D1 C1
D1 C1

 -
-  и
и 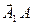 -
-  +
+  +
+ 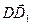
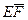 через векторы
через векторы  и
и 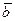 .
.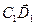 =
= 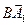 =
= 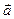 -
- 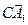
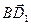 по векторам
по векторам 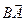 ,
, 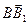
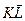
 -
- 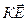 -
- 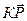 через вектор
через вектор