
|
|
Таким образом, ускорение а есть векторная величина, равная первой производной скорости по времени.Разложим вектор Dv на две составляющие. Для этого из точки А (рис. 4) по направлению скорости v отложим вектор Тангенциальная составляющая ускорения –составляющая полного ускорения тела криволинейного движения материальной точки, которая характеризует численное изменение скорости и направленно по касательной в сторону отправления движения. - нормальное и тангенсуальное ускорение взаимоперпендикулярны.
т. е. равна первой производной по времени от модуля скорости, определяя тем самым быстроту изменения скорости по модулю. Найдем вторую составляющую ускорения. Допустим, что точка В достаточно близка к точке А, поэтому Ds можно считать дугой окружности некоторого радиуса г, мало отличающейся от хорды АВ. Тогда из подобия треугольников АОВ и EAD следует
Поскольку v1 = v, угол EAD стремится к нулю, а так как треугольник EAD равнобедренный, то угол ADE между v и Dvn стремится к прямому. Следовательно, при Dt ® 0 векторы Dvn и v оказываются взаимно перпендикулярными. Так как вектор скорости направлен по касательной к траектории, то вектор Dvn, перпендикулярный вектору скорости, направлен к центру ее кривизны. Вторая составляющая ускорения, равная
называется нормальной составляющей ускорения (составляющая полного ускорения тела (центростремительного) криволинейного движения материальной точки, которая характеризует быстроту изменения скорости по направлению и направлена по главной нормали траектории движения в сторону центра кривизны) поэтому ее называют также центростремительным ускорением). Полное ускорение тела есть геометрическаясумма тангенциальной и нормальной составляющих (рис.5):
Формула пути при равномерном движении.. Скоростью равномерного прямолинейного движения называют векторную величину, равную отношению перемещения тела к промежутку времени, в течение которого было совершено это перемещение: v=s/t. Формула перемещения при равноускоренном движении используется при доказательстве теоремы о кинетической энергии. Для этого необходимо перенести ускорение в левую часть и домножить обе части на массу тела:
Записав аналогичные соотношения для координат y и z и просуммировав все три равенства получим соотношение:
Слева стоит работа постоянной равнодействующей силы 22.Ламинарное и турбулентное течения жидкости. Число рейнольдса. Уравнение неразрывности для несжимаемой жидкости. Ламина́рное тече́ние (лат. lāmina — «пластинка») — течение, при котором жидкость или газ перемещается слоями без перемешивания и пульсаций (то есть беспорядочных быстрых изменений скорости и давления). Только в ламинарном режиме возможно получение точных решений уравнения движения жидкости (уравнений Навье-Стокса), например течение Пуазейля. ТУРБУЛЕНТНОЕ ТЕЧЕНИЕ (от латинского turbulentus - бурный, беспорядочный), течение жидкости или газа, при котором частицы жидкости совершают неупорядоченные, хаотические движения по сложным траекториям, а скорость, температура, давление и плотность среды испытывают хаотические флуктуации. Отличается от ламинарного течения интенсивным перемешиванием, теплообменом, большими значениями коэффициент трения и пр. В природе и технике большинство течений жидкости и газов - турбулентные течения.
Турбулентное течение отличаются от соответствующих ламинарных течений как своей сложной внутренней структурой (рис. 1), так и распределением осреднённой скорости по сечению потока и интегральными характеристиками — зависимостью средней по сечению или максимальной скорости, расхода, а также коэффициента сопротивления от Рейнольдса числа Re. Число, или, правильнее, критерий Рейно́льдса (), — безразмерная величина, характеризующая отношение нелинейного и диссипативного членов в уравнении Навье-Стокса[1]. Число Рейнольдса также считается критерием подобия течения вязкой жидкости. Число Рейнольдса определяется следующим соотношением:
где § § § § § § § 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , по модулю равный v1. Очевидно, что вектор
, по модулю равный v1. Очевидно, что вектор 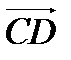 , равный Dvt, определяет изменение скорости за время Dt по модулю: Dvt = v1 - v. Вторая же составляющая Dvn вектора Dv характеризует изменение скорости за время Dt по направлению.
, равный Dvt, определяет изменение скорости за время Dt по модулю: Dvt = v1 - v. Вторая же составляющая Dvn вектора Dv характеризует изменение скорости за время Dt по направлению.
 ,но так как AB=vDt, то
,но так как AB=vDt, то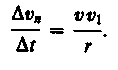 В пределе при Dt ® 0 получим v1 ® v.
В пределе при Dt ® 0 получим v1 ® v.

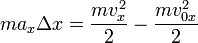 .
.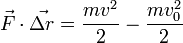 .
. , а справа — разность кинетических энергий в конечный и начальный момент движения.
, а справа — разность кинетических энергий в конечный и начальный момент движения.
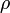 — плотность среды, кг/м3;
— плотность среды, кг/м3; — характерная скорость, м/с;
— характерная скорость, м/с; — характерный размер, м;
— характерный размер, м; — динамическая вязкость среды, Н·с/м2;
— динамическая вязкость среды, Н·с/м2; — кинематическая вязкость среды, м2/с(
— кинематическая вязкость среды, м2/с( 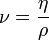 ) ;
) ; — объёмная скорость потока;
— объёмная скорость потока; — площадь сечения трубы.
— площадь сечения трубы.