
|
|
Интерференция в тонких плёнках
При освещении тонкой плёнки можно наблюдать интерференцию световых волн, отражённых от верхней и нижней поверхности плёнок (рис. 4.16). Для белого света, представляющего собой смешение электромагнитных волн из всего оптического спектра интерференционные полосы приобретают окраску. Это явление получило название цветов тонких плёнок. Цвета тонких плёнок наблюдаются на стенках мыльных пузырьков, на плёнках масла, нефти, на поверхности металлов при их закалке (цвета побежалости).
Для объяснения этих явлений рассмотрим расположенную в вакууме плоско параллельную диэлектрическую пластинку (рис.) толщины
волна, отражённая от верней поверхности в вакууме, приобретающая дополнительный набег фазы
где
При условии, что
кратно целому числу
Аналогичным образом получим условия минимума интерференционной картины в точке наблюдения
где
Интерференционная картина, образованная отражёнными под разными углами плоскими волнами от поверхностей плоско параллельной пластинки / плёнки, получила название интерференционных полос равного наклона. В этом названии отражается тот факт, наблюдаемая интерференционная картина образована параллельно распространяющимися волнами, падающими на пластинку под одним углом / наклоном. Область наблюдения интерференции расположена в бесконечности, где "пересекаются" параллельные лучи. Углы, в направлении которых формируются максимумы и минимумы интерференционной картины в соответствии с (4.24) зависят от длины волны. Это объясняет окраску интерференционной картины световых лучей, отражённых от поверхностей плоско параллельной пластинки при её облучении белым светом.
Для наблюдения интерференционной картины полос равного наклона на конечном расстоянии от пластинки используется линза (рис. 4.17). Благодаря свойству линзы параллельные световые лучи сходятся в некоторой точке фокальной плоскости. Эта точка совпадает с фокусом линзы, если лучи параллельны главной оптической оси. В силу зависимости (4.24) направления на главные максимумы и минимумы от длины волны, в фокальной плоскости линзы можно наблюдать окрашенную в цвета оптического спектра интерференционную картину полос равного наклона.
Другой вид интерференции света в тонких плёнках, толщина которых меняется её по поперечному сечению, получил название интерференционных полос равной толщины. Для изучения этого явления рассмотрим плёнку переменной толщины в виде клина (рис. 4.18). Рассмотрим падающую на поверхность диэлектрического клина с показателем преломления
Отражённые от верхней и нижней граней клина плоские волны I' и I" (рис. 4.18) пересекутся вблизи поверхности клина из-за не параллельности его граней . Следовательно, при помещении экрана вблизи поверхности клина можно наблюдать интерференционную картину в виде полос, параллельных ребру клина, которую образуют волны, отразившиеся от его граней в тех точках их поверхности, где клин имеет одинаковую толщину. Это объясняет названия рассматриваемого явления. При облучении поверхности клина белым светом интерференционная картина в виде полос равной толщины оказывается окрашенной в цвета оптического спектра. Для наблюдения интерференционной картины в виде полос равной толщины используется линза (рис. 4.19), назначение которой состоит в увеличении изображения интерференционной картины, для её визуального наблюдения.
Интерференционная картина в виде полос равной толщины широко используется на практике для контроля степени неровности различных поверхностей, плёнок, а также всевозможных покрытий. Если поверхности плёнки неровные, то полосы равной толщины принимают неправильную причудливую форму, связанную с соответствующим контуром равной толщины плёнки.
Для получения количественных соотношений, характерных для рассматриваемого явления , рассмотрим расчёт интерференционной картины в виде колец Ньютона, которая имеет место при освещении плоской монохроматической световой волной с длиной волны
Найдём оптическую разность хода волн, отражённых от нижней поверхности линзы и от поверхности зеркала. Для облегчения расчётов заменим внутреннюю криволинейную поверхность линзы в точке отражения луча плоскостью, параллельной отражающей поверхности (рис. 4.20). В результате такого упрощения удаётся свести расчёт интерференционной картины в виде колец Ньютона к расчёту интерференционной картины в виде полос равной толщины. Полосы представляют собой концентрические эллипсы при наклонном падении света на линзу или окружности при нормальном падении. Как следует из приведенных выше рассуждений о возможности наблюдения полос равной толщины, соответствующая интерференционная картина наблюдается вблизи поверхности плёнки. В первом приближении можно полагать, что наблюдаемые интерференционные полосы располагаются непосредственно на поверхности плёнки в точке отражения волны. Тогда радиусы колец Ньютона
радиусам окружностей, каждая из которых соответствует точкам нижней поверхности линзы, находящихся на одинаковом расстоянии
Радиусы колец Ньютона
где
Чётным значениям
увеличения проходимого лучами пути интерференционные кольца, каждое из которых соответствует некоторой постоянной разности хода, будет стягиваться к центру. При этом центр картины по мере поднятия линзы будет становиться попеременно то светлым, то тёмным. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
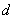 с показателем преломления
с показателем преломления  , где
, где 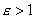 - диэлектрическая проницаемость диэлектрика освещаемую плоской световой монохроматической волной с длиной волны
- диэлектрическая проницаемость диэлектрика освещаемую плоской световой монохроматической волной с длиной волны  под углом
под углом 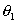 (рис. 4.16). При отражении световых волн от верхней и нижней поверхности пластинки между отражёнными волнами возникнет оптическая разность хода
(рис. 4.16). При отражении световых волн от верхней и нижней поверхности пластинки между отражёнными волнами возникнет оптическая разность хода  , которая является следствием того факта, что волна, отражённая от нижней поверхности пластинки проходит больший путь внутри диэлектрической пластинки, чем
, которая является следствием того факта, что волна, отражённая от нижней поверхности пластинки проходит больший путь внутри диэлектрической пластинки, чем
 при отражении от оптически более плотной среды. Из геометрических соображений следует, что:
при отражении от оптически более плотной среды. Из геометрических соображений следует, что: ,
,
 - угол преломления падающего светового пучка пластинкой (рис. 4.16), связанного с углом падения
- угол преломления падающего светового пучка пластинкой (рис. 4.16), связанного с углом падения 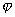 соотношением следующим из закона Снеллиуса:
соотношением следующим из закона Снеллиуса:  .
.
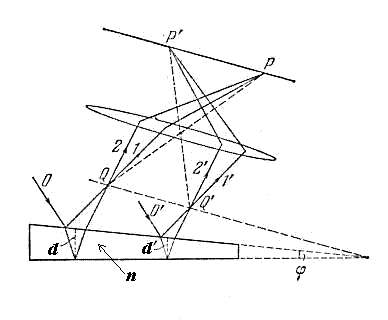
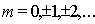 ... длин волн, в точке наблюдения
... длин волн, в точке наблюдения  на расстоянии от поверхности плёнки во много раз большем, чем толщина пластинки, отражённые от обеих поверхностей пластинки волны будут складываться в фазе и формировать интерференционный максимум.
на расстоянии от поверхности плёнки во много раз большем, чем толщина пластинки, отражённые от обеих поверхностей пластинки волны будут складываться в фазе и формировать интерференционный максимум. ,
,


 (рис. 4.20) равны
(рис. 4.20) равны
 - радиус кривизны линзы, а
- радиус кривизны линзы, а  , то (рис. 4.20)
, то (рис. 4.20)
 .
.
 , соответствующих интерференционным максимумам с номерами
, соответствующих интерференционным максимумам с номерами  , получающихся при нормальном падении световой волны к поверхности пластинки можно найти из (4.24a)при
, получающихся при нормальном падении световой волны к поверхности пластинки можно найти из (4.24a)при 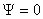 и
и 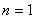 с учётом (4.24b):
с учётом (4.24b): ,
,
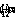 - длина световой волны, освещающей линзу.
- длина световой волны, освещающей линзу.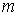 соответствуют светлые кольца, а нечётным - тёмные (рис. 4.21). В частности в центре картины
соответствуют светлые кольца, а нечётным - тёмные (рис. 4.21). В частности в центре картины  будет находиться тёмное кольцо, вырождающееся в тёмную точку и соответствующее направлению противофазного сложения интерферирующих волн. Если линзу при наблюдении колец Ньютона поднимать вертикально вверх, то из-за
будет находиться тёмное кольцо, вырождающееся в тёмную точку и соответствующее направлению противофазного сложения интерферирующих волн. Если линзу при наблюдении колец Ньютона поднимать вертикально вверх, то из-за