|
Поглощение (абсорбция) света
Поглощением (абсорбцией) света называется явление потери энергии световой волной, проходящей через вещество.
Свет поглощается в тех случаях, когда проходящая волна затрачивает энергию на различные процессы. Среди них: преобразование энергии волны во внутреннюю энергию – при нагревании вещества; затраты энергии на вторичное излучение в другом диапазоне частот (фотолюминесценция); затраты энергии на ионизацию – при фотохимических реакциях и т.п. При поглощении света колебания затухают и амплитуда электрической составляющей уменьшается по мере распространения волны. Для плоской волны, распространяющейся вдоль оси x, имеем
 . .
Здесь E(x) – амплитудное значение напряженности электрического поля волны в точках с координатой x;  – амплитуда в точке с координатой x = 0; t – время, за которое волна распространилась на расстояние, равное x; β – коэффициент затухания колебаний; – амплитуда в точке с координатой x = 0; t – время, за которое волна распространилась на расстояние, равное x; β – коэффициент затухания колебаний;  коэффициент поглощения, зависящий от химической природы среды и от длины волны проходящего света. коэффициент поглощения, зависящий от химической природы среды и от длины волны проходящего света.
Интенсивность волны будет изменяться по закону Бугера (П. Бугер (1698 – 1758) – французский ученый):
 , ,
где  – интенсивность волны на входе в среду. – интенсивность волны на входе в среду.
При  , ,  . Следовательно, коэффициент поглощения – физическая величина, численно равная обратному значению толщины слоя вещества, в котором интенсивность волны убывает в е = 2,72 раз. . Следовательно, коэффициент поглощения – физическая величина, численно равная обратному значению толщины слоя вещества, в котором интенсивность волны убывает в е = 2,72 раз.
Зависимость коэффициента поглощения от длины волны определяет спектр поглощения материала. В веществе (например в газе) может присутствовать несколько сортов частиц, участвующих в колебаниях под действием распространяющейся электромагнитной волны. Если эти частицы слабо взаимодействуют, то коэффициент поглощения мал для широкого спектра частот, и лишь в узких областях он резко возрастает (рис. 10.7, а).

| | а
| б
| Рис. 10.7
Эти области соответствуют частотам собственных колебаний оптических электронов в атомах разных видов. Спектр поглощения таких веществ линейчатый и представляет собою темные полосы на радужной окраске спектра, если это видимая область. При увеличении давления газа полосы поглощения уширяются. В жидком состоянии они сливаются, и спектр поглощения принимает вид, показанный на рис. 10.7, б. Причиной уширения является усиление связи атомов (молекул) в среде.
Коэффициент поглощения, зависящий от длины волны λ (или частоты ω), для различных веществ различен. Например, одноатомные газы и пары металлов (т.е. вещества, в которых атомы расположены на значительных расстояниях друг от друга и их можно считать изолированными) обладают близким к нулю коэффициентом поглощения, и лишь для очень узких спектральных областей (примерно  м) наблюдаются резкие максимумы (так называемый линейчатый спектр поглощения). Эти линии соответствуют частотам собственных колебаний электронов в атомах. Спектр поглощения молекул, определяемый колебаниями атомов в молекулах, характеризуется полосами поглощения (примерно м) наблюдаются резкие максимумы (так называемый линейчатый спектр поглощения). Эти линии соответствуют частотам собственных колебаний электронов в атомах. Спектр поглощения молекул, определяемый колебаниями атомов в молекулах, характеризуется полосами поглощения (примерно  м). м).
Коэффициент поглощения для диэлектриков невелик (примерно  ), однако у них наблюдается селективное поглощение света в определенных интервалах длин волн, когда α резко возрастает и наблюдаются сравнительно широкие полосы поглощения (примерно ), однако у них наблюдается селективное поглощение света в определенных интервалах длин волн, когда α резко возрастает и наблюдаются сравнительно широкие полосы поглощения (примерно  м), т.е. диэлектрики имеют сплошной спектр поглощения. Это связано с тем, что в диэлектриках нет свободных электронов и поглощение света обусловлено явлением резонанса при вынужденных колебаниях электронов в атомах и атомов в молекулах диэлектрика. м), т.е. диэлектрики имеют сплошной спектр поглощения. Это связано с тем, что в диэлектриках нет свободных электронов и поглощение света обусловлено явлением резонанса при вынужденных колебаниях электронов в атомах и атомов в молекулах диэлектрика.
Коэффициент поглощения для металлов имеет большие значения (примерно  ), и поэтому металлы практически непрозрачны для света. В металлах из-за наличия свободных электронов, движущихся под действием электрического поля световой волны, возникают быстропеременные токи, сопровождающиеся выделением джоулевой теплоты. Поэтому энергия световой волны быстро уменьшается, превращаясь во внутреннюю энергию металла. Чем выше проводимость металла, тем сильнее в нем поглощение света. ), и поэтому металлы практически непрозрачны для света. В металлах из-за наличия свободных электронов, движущихся под действием электрического поля световой волны, возникают быстропеременные токи, сопровождающиеся выделением джоулевой теплоты. Поэтому энергия световой волны быстро уменьшается, превращаясь во внутреннюю энергию металла. Чем выше проводимость металла, тем сильнее в нем поглощение света.
На рис. 10.8 представлена типичная зависимость коэффициента поглощения α от частоты света ν и зависимость показателя преломления n от ν в области полосы поглощения. Из рисунка следует, что внутри полосы поглощения наблюдается аномальная дисперсия (n убывает с увеличением ν). Однако поглощение вещества должно быть значительным, чтобы повлиять на ход показателя преломления.

Рис. 10.8
Зависимостью коэффициента поглощения от частоты (длины волны) объясняется окрашенность поглощающих тел. Например, стекло, слабо поглощающее красные и оранжевые лучи и сильно поглощающее зеленые и синие, при освещении белым светом будет казаться красным. Если на такое стекло направить зеленый и синий свет, то из-за сильного поглощения света этих длин волн стекло будет казаться черным. Это явление используется для изготовления светофильтров, которые в зависимости от химического состава (стекла с присадками различных солей; пленки из пластмасс, содержащие красители; растворы красителей и т. д.) пропускают свет только определенных длин волн, поглощая остальные. Разнообразие пределов селективного (избирательного) поглощения у различных веществ объясняет разнообразие и богатство цветов и красок, наблюдающееся в окружающем мире.
Спектральный анализ позволяет получить информацию о составе Солнца, поскольку определенный набор спектральных линий исключительно точно характеризует химический элемент. Так, с помощью наблюдений спектра Солнца был открыт гелий.
Видимая часть солнечного излучения при изучении с помощью спектроанализирующих приборов оказывается неоднородной – в спектре наблюдаютсялинии поглощения,впервые описанные в 1814 году И. Фраунгофером.

Рис. 10.9
С помощью спектрального анализа узнали, что звезды состоят из тех же самых элементов, которые имеются и на Земле.
Явление поглощения широко используется в абсорбционном спектральном анализе смеси газов, основанном на измерениях спектров частот и интенсивностей линий (полос) поглощения. Структура спектров поглощения определяется составом и строением молекул, поэтому изучение спектров поглощения является одним из основных методов количественного и качественного исследования веществ.
Вопрос
Закон Максвелла о распределении молекул идеального газа по скоростям и энергиям теплового движения При выводе основного уравнения молекулярно-кинетической теории молекулам задавали различные скорости. В результате многократных соударений скорость каждой молекулы изменяется по модулю и направлению. Однако из-за хаотического движения молекул все направления движения являются равновероятными, т. е. в любом направлении в среднем движется одинаковое число молекул.По молекулярно-кинетической теории, как бы ни изменялись скорости молекул при столкновениях, средняя квадратичная скорость молекул массой т0 в газе, находящемся в состоянии равновесия при Т= const. остается постоянной и равной  Это объясняется тем, что в газе, находящемся в состоянии равновесия, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям, которое подчиняется вполне определенному статистическому закону. Этот закон теоретически выведен Дж. Максвеллом.При выводе закона распределения молекул по скоростям Максвелл предполагал, что газ состоит из очень большого числа N тождественных молекул, находящихся в состоянии беспорядочного теплового движения при одинаковой температуре. Предполагалось также, что силовые поля на газ не действуют.Закон Максвелла описывается некоторой функцией f(v), называемой функцией распределения молекул по скоростям. Если разбить диапазон скоростей молекул на малые интервалы, равные dv, то на каждый интервал скорости будет приходиться некоторое число молекул dN(v), имеющих скорость, заключенную в этом интервале. Функция f(v) определяет относительное число молекул dN(v)/N, скорости которых лежат в интервале от v до v+dv, т. е. Это объясняется тем, что в газе, находящемся в состоянии равновесия, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям, которое подчиняется вполне определенному статистическому закону. Этот закон теоретически выведен Дж. Максвеллом.При выводе закона распределения молекул по скоростям Максвелл предполагал, что газ состоит из очень большого числа N тождественных молекул, находящихся в состоянии беспорядочного теплового движения при одинаковой температуре. Предполагалось также, что силовые поля на газ не действуют.Закон Максвелла описывается некоторой функцией f(v), называемой функцией распределения молекул по скоростям. Если разбить диапазон скоростей молекул на малые интервалы, равные dv, то на каждый интервал скорости будет приходиться некоторое число молекул dN(v), имеющих скорость, заключенную в этом интервале. Функция f(v) определяет относительное число молекул dN(v)/N, скорости которых лежат в интервале от v до v+dv, т. е. 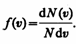 Применяя методы теории вероятностей. Максвелл нашел функцию f(v) — закон о распределеня молекул идеального газа по скоростям: Применяя методы теории вероятностей. Максвелл нашел функцию f(v) — закон о распределеня молекул идеального газа по скоростям:  Относительное число молекул dN(v)/N, скорости которых лежат в интервале от v до v+dv, находится как площадь заштрихованной полоски на рис. 65. Площадь, ограниченная кривой распределения и осью абсцисс, равна единице. Это означает, что функция f(v) удовлетворяет условию нормировки Относительное число молекул dN(v)/N, скорости которых лежат в интервале от v до v+dv, находится как площадь заштрихованной полоски на рис. 65. Площадь, ограниченная кривой распределения и осью абсцисс, равна единице. Это означает, что функция f(v) удовлетворяет условию нормировки  Скорость, при которой функция распределения молекул идеального газа по скоростям максимальна, называется наиболее вероятной скоростью. Значение наиболее вероятной скорости можно найти продифференцировав выражение (44.1) (постоянные множители опускаем) по аргументу v, приравняв результат нулю и используя условие для максимума выражения f(v): Значения v=0 и v=¥ соответствуют минимумам выражения . Скорость, при которой функция распределения молекул идеального газа по скоростям максимальна, называется наиболее вероятной скоростью. Значение наиболее вероятной скорости можно найти продифференцировав выражение (44.1) (постоянные множители опускаем) по аргументу v, приравняв результат нулю и используя условие для максимума выражения f(v): Значения v=0 и v=¥ соответствуют минимумам выражения .  Средняя скорость молекулы <v> (средняя арифметическая скорость) определяется по формуле Средняя скорость молекулы <v> (средняя арифметическая скорость) определяется по формуле  Подставляя сюда f(v) и интегрируя, получаем Подставляя сюда f(v) и интегрируя, получаем  Скорости, характеризующие состояние газа: 1) наиболее вероятная Скорости, характеризующие состояние газа: 1) наиболее вероятная  2) средняя 2) средняя  3) средняя квадратичная 3) средняя квадратичная 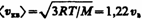 . Исходя из распределения молекул по скоростям . Исходя из распределения молекул по скоростям  можно найти распределение молекул газа по значениям кинетической энергии e. Для этого перейдем от переменной v к переменной e=m0v2/2. Подставив в v= можно найти распределение молекул газа по значениям кинетической энергии e. Для этого перейдем от переменной v к переменной e=m0v2/2. Подставив в v=  и dv= и dv=  de de  где dN(e) — число молекул, имеющих кинетическую энергию поступательного движения, заключенную в интервале от e до e + de. Таким образом, функция распределения молекул по энергиям теплового движения где dN(e) — число молекул, имеющих кинетическую энергию поступательного движения, заключенную в интервале от e до e + de. Таким образом, функция распределения молекул по энергиям теплового движения 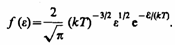 Средняя кинетическая энергия <e> молекулы идеального газа Средняя кинетическая энергия <e> молекулы идеального газа 
Вопрос 36
Полная энергия термодинамической системы представляет собой сумму кинетической энергии движения всех тел, входящих в систему, потенциальной энергии взаимодействия их между собой и с внешними телами и энергии, содержащейся внутри тел системы. Если из полной энергии вычесть кинетическую энергию, характеризующую макроскопическое движение системы как целого, и потенциальную энергию взаимодействия её тел с внешними макроскопическими телами, то оставшаяся часть будет представлять собой внутреннюю энергию термодинамической системы. Внутренняя энергия термодинамической системы включает в себя энергию микроскопического движения и взаимодействия частиц системы, а так же их внутримолекулярную и внутриядерную энергии.Полная энергия системы (а, следовательно, и внутренняя энергия) также как потенциальная энергия тела в механике может быть определена с точностью до произвольной константы. Поэтому, если любые макроскопические движения в системе и взаимодействия её с внешними телами отсутствуют, можно принять "макроскопические" составляющие кинетической и потенциальной энергий равными нулю и считать внутреннюю энергию системы равной её полной энергии. Такая ситуация имеет место в случае, когда система находится в состоянии термодинамического равновесия. Введём характеристику состояния термодинамического равновесия - температуру. Так называется величина, зависящая от параметров состояния, например, от давления и объёма газа, и являющаяся функцией внутренней энергии системы. Эта функция обычно имеет монотонную зависимость от внутренней энергии системы, то есть растёт с ростом внутренней энергии. Температура термодинамических систем, находящихся в состоянии равновесия, обладает следующими свойствами:Если две равновесные термодинамические системы, находятся в тепловом контакте и имеют одинаковую температуру, то совокупная термодинамическая система находится в состоянии термодинамического равновесия при той же температуре. Если какая-либо равновесная термодинамическая система имеет одну и ту же температуру с двумя другими системами, то эти три системы находятся в термодинамическом равновесии при одной и той же температуре. Таким образом, температура есть мера состояния термодинамического равновесия. Для установления этой меры уместно ввести понятие теплопередачи. Теплопередачей называется передача энергии от одного тела к другому без переноса вещества и совершения механической работы.Если между телами, находящимися в тепловом контакте друг с другом, теплопередача отсутствует, то тела имеют одинаковые температуры и находятся в состоянии термодинамического равновесия друг с другом. Если в изолированной системе, состоящей из двух тел, эти тела находятся при разных температурах, то теплопередача будет осуществляться таким образом, чтобы энергия передавалась от более нагретого тела менее нагретому. Этот процесс будет продолжаться до тех пор, пока температуры тел не сравняются, и изолированная система из двух тел не достигнет состояния термодинамического равновесия. Для возникновения процесса теплопередачи необходимо создание потоков теплоты, то есть требуется выход из состояния теплового равновесия. Поэтому равновесная термодинамика не описывает процесс теплопередачи, а только его результат - переход в новое равновесное состояние. Описание самого процесса теплопередачи выполнено в шестой главе, посвящённой физической кинетике.2 часть вопроса В механике введилось понятие числа степеней свободы: это число независимых переменных (координат), которые полностью определяют положение системы в пространстве. В некоторых задачах молекулу одноатомного газа (рис. 1, а) рассматривают как материальную точку, которой задают три степени свободы поступательного движения. При этом не учитывается энергия вращательного движения. В механике молекула двухатомного газа в первом приближении считается совокупностью двух материальных точек, которые жестко связанны недеформируемой связью (рис. 1, б). Данная система кроме трех степеней свободы поступательного движения имеет еще две степени свободы вращательного движения. Вращение вокруг третьей оси, проходящей через оба атома, лишено смысла. Значит, у двухатомного газа пять степеней свободы (i = 5). У трехатомной (рис. 1, в) и многоатомной нелинейной молекулы шесть степеней свободы: три поступательных и три вращательных. Естественно считать, что жесткой связи между атомами не существует. Поэтому необходимо учитывать для реальных молекул также степени свободы колебательного движения.

При любом числе степеней свободы данной молекулы три степени свободы всегда поступательные. Ни одна из поступательных степеней свободы не имеет преимущества перед другими, значит на каждую из них приходится в среднем одинаковая энергия, равная 1/3 значения <ε0> (энергия поступательного движения молекул):  В статистической физике выводится закон Больцмана о равномерном распределении энергии по степеням свободы молекул: для статистической системы, которая находится в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная kT/2, а на каждую колебательную степень свободы — в среднем энергия, равная kT. Колебательная степень обладает вдвое большей энергией, т.к. на нее приходится как кинетическая энергия (как в случае поступательного и вращательного движений), так и потенциальная, причем средние значения потенциальной и кинетической и энергии одинаковы. Значит, средняя энергия молекул. В статистической физике выводится закон Больцмана о равномерном распределении энергии по степеням свободы молекул: для статистической системы, которая находится в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная kT/2, а на каждую колебательную степень свободы — в среднем энергия, равная kT. Колебательная степень обладает вдвое большей энергией, т.к. на нее приходится как кинетическая энергия (как в случае поступательного и вращательного движений), так и потенциальная, причем средние значения потенциальной и кинетической и энергии одинаковы. Значит, средняя энергия молекул.  где i — сумма числа поступательных, числа вращательных в удвоенного числа колебательных степеней свободы молекулы: i=iпост+iвращ+2iколеб В классической теории рассматривают молекулы с жесткой связью между атомами; для них i совпадает с числом степеней свободы молекулы. где i — сумма числа поступательных, числа вращательных в удвоенного числа колебательных степеней свободы молекулы: i=iпост+iвращ+2iколеб В классической теории рассматривают молекулы с жесткой связью между атомами; для них i совпадает с числом степеней свободы молекулы.  Так как в идеальном газе взаимная потенциальная энергия взаимодействия молекул равна нулю (молекулы между собой не взаимодействуют), то внутренняя энергия для одного моля газа, будет равна сумме кинетических энергий NA молекул: Внутренняя энергия для произвольной массы m газ Так как в идеальном газе взаимная потенциальная энергия взаимодействия молекул равна нулю (молекулы между собой не взаимодействуют), то внутренняя энергия для одного моля газа, будет равна сумме кинетических энергий NA молекул: Внутренняя энергия для произвольной массы m газ  а . где М — молярная масса, ν — количество вещества. а . где М — молярная масса, ν — количество вещества.
Вопрос 37
Первое начало термодинамики — один из трёх основных законов термодинамики, представляет собой закон сохранения энергии для термодинамических систем.Первое начало термодинамики было сформулировано в середине XIX века в результате работ немецкого учёного Ю. Р. Майера, английского физика Дж. П. Джоуля и немецкого физика Г. Гельмгольца[1]. Согласно первому началу термодинамики, термодинамическая система может совершать работу только за счёт своей внутренней энергии или каких-либо внешних источников энергии. Первое начало термодинамики часто формулируют как невозможность существования вечного двигателя первого рода, который совершал бы работу, не черпая энергию из какого-либо источника. ФормулировкаСуществует несколько эквивалентных формулировок первого начала термодинамики В любой изолированной системе запас энергии остаётся постоянным.[2] Это — формулировка Дж. П. Джоуля (1842 г.).Количество теплоты, полученное системой, идёт на изменение её внутренней энергии и совершение работы против внешних сил  Изменение внутренней энергии системы при переходе её из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе, то есть, оно зависит только от начального и конечного состояния системы и не зависит от способа, которым осуществляется этот переход. Это определение особенно важно для химической термодинамики[2] (ввиду сложности рассматриваемых процессов). Иными словами, внутренняя энергия является функцией состояния. В циклическом процессе внутренняя энергия не изменяется. Изменение внутренней энергии системы при переходе её из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе, то есть, оно зависит только от начального и конечного состояния системы и не зависит от способа, которым осуществляется этот переход. Это определение особенно важно для химической термодинамики[2] (ввиду сложности рассматриваемых процессов). Иными словами, внутренняя энергия является функцией состояния. В циклическом процессе внутренняя энергия не изменяется.  Для элементарного количества теплоты Для элементарного количества теплоты  элементарной работы элементарной работы  и малого приращения и малого приращения  внутренней энергии первый закон термодинамики имеет вид внутренней энергии первый закон термодинамики имеет вид  Разделение работы на две части, одна из которых описывает работу, совершённую над системой, а вторая — работу, совершённую самой системой, подчёркивает, что эти работы могут быть совершены силами Разделение работы на две части, одна из которых описывает работу, совершённую над системой, а вторая — работу, совершённую самой системой, подчёркивает, что эти работы могут быть совершены силами  разной природы вследствие разных источников сил. Важно заметить, что разной природы вследствие разных источников сил. Важно заметить, что   являются полными дифференциалами, а являются полными дифференциалами, а   — нет.Теплоёмкость тела (обычно обозначается латинской буквой C) — физическая величина, определяющая отношение бесконечно малого количества теплоты δQ, полученного телом, к соответствующему приращению его температуры δT: — нет.Теплоёмкость тела (обычно обозначается латинской буквой C) — физическая величина, определяющая отношение бесконечно малого количества теплоты δQ, полученного телом, к соответствующему приращению его температуры δT:  Единица измерения теплоёмкости в системе СИ — Дж/К. Удельная теплоёмкость Удельной теплоёмкостью называется теплоёмкость, отнесённая к единичному количеству вещества. Количество вещества может быть измерено в килограммах, кубических метрах и молях. В зависимости от того, к какой количественной единице относится теплоёмкость, различают массовую, объёмную и молярную теплоёмкость.Массовая теплоёмкость (С) — это количество теплоты, которое необходимо подвести к единице массы вещества, чтобы нагреть его на единицу температуры. В СИ измеряется в джоулях на килограмм на кельвин (Дж·кг−1·К−1).Объёмная теплоёмкость (С′) — это количество теплоты, которое необходимо подвести к единице объёма вещества, чтобы нагреть его на единицу температуры. В СИ измеряется в джоулях на кубический метр на кельвин (Дж·м−3·К−1).Молярная теплоёмкость (Сμ) — это количество теплоты, которое необходимо подвести к 1 молю вещества, чтобы нагреть его на единицу температуры. В СИ измеряется в джоулях на моль на кельвин (Дж/(моль·К)). Теплоёмкость для различных состояний вещества Понятие теплоёмкости определено как для веществ в различных агрегатных состояниях (твёрдых тел, жидкостей, газов), так и для ансамблей частиц и квазичастиц (в физике металлов, например, говорят о теплоёмкости электронного газа).Для примера, в молекулярно-кинетической теории газов показывается, что молярная теплоёмкость идеального газа с i степенями свободы при постоянном объёме (для одного моля идеального газа) равна: Единица измерения теплоёмкости в системе СИ — Дж/К. Удельная теплоёмкость Удельной теплоёмкостью называется теплоёмкость, отнесённая к единичному количеству вещества. Количество вещества может быть измерено в килограммах, кубических метрах и молях. В зависимости от того, к какой количественной единице относится теплоёмкость, различают массовую, объёмную и молярную теплоёмкость.Массовая теплоёмкость (С) — это количество теплоты, которое необходимо подвести к единице массы вещества, чтобы нагреть его на единицу температуры. В СИ измеряется в джоулях на килограмм на кельвин (Дж·кг−1·К−1).Объёмная теплоёмкость (С′) — это количество теплоты, которое необходимо подвести к единице объёма вещества, чтобы нагреть его на единицу температуры. В СИ измеряется в джоулях на кубический метр на кельвин (Дж·м−3·К−1).Молярная теплоёмкость (Сμ) — это количество теплоты, которое необходимо подвести к 1 молю вещества, чтобы нагреть его на единицу температуры. В СИ измеряется в джоулях на моль на кельвин (Дж/(моль·К)). Теплоёмкость для различных состояний вещества Понятие теплоёмкости определено как для веществ в различных агрегатных состояниях (твёрдых тел, жидкостей, газов), так и для ансамблей частиц и квазичастиц (в физике металлов, например, говорят о теплоёмкости электронного газа).Для примера, в молекулярно-кинетической теории газов показывается, что молярная теплоёмкость идеального газа с i степенями свободы при постоянном объёме (для одного моля идеального газа) равна: 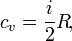 где R ≈ 8,31 Дж/(моль·К) — универсальная газовая постоянная. А при постоянном давлении где R ≈ 8,31 Дж/(моль·К) — универсальная газовая постоянная. А при постоянном давлении  Удельные теплоёмкости многих веществ приведены в справочниках обычно для процесса при постоянном давлении. К примеру, удельная теплоёмкость жидкой воды при нормальных условиях — 4200 Дж/(кг·К); льда — 2100 Дж/(кг·К). Теория теплоёмкости Сравнение моделей Дебая и Эйнштейна для теплоёмкости твёрдого тела Существует несколько теорий теплоёмкости твердого тела:Закон Дюлонга — Пти и закон Джоуля — Коппа. Оба закона выведены из классических представлений и с определенной точностью справедливы лишь для нормальных температур (примерно от 15 °C до 100 °C).Квантовая теория теплоёмкостей Эйнштейна. Первое применение квантовых законов к описанию теплоёмкости.Квантовая теория теплоёмкостей Дебая. Содержит наиболее полное описание и хорошо согласуется с экспериментом.Теплоёмкость системы невзаимодействующих частиц (например, газа) определяется числом степеней свободы частиц. Удельные теплоёмкости многих веществ приведены в справочниках обычно для процесса при постоянном давлении. К примеру, удельная теплоёмкость жидкой воды при нормальных условиях — 4200 Дж/(кг·К); льда — 2100 Дж/(кг·К). Теория теплоёмкости Сравнение моделей Дебая и Эйнштейна для теплоёмкости твёрдого тела Существует несколько теорий теплоёмкости твердого тела:Закон Дюлонга — Пти и закон Джоуля — Коппа. Оба закона выведены из классических представлений и с определенной точностью справедливы лишь для нормальных температур (примерно от 15 °C до 100 °C).Квантовая теория теплоёмкостей Эйнштейна. Первое применение квантовых законов к описанию теплоёмкости.Квантовая теория теплоёмкостей Дебая. Содержит наиболее полное описание и хорошо согласуется с экспериментом.Теплоёмкость системы невзаимодействующих частиц (например, газа) определяется числом степеней свободы частиц.
Вопрос 38
Изопроцессы — термодинамические процессы, во время которых количество вещества и ещё одна из физических величин — параметров состояния: давление, объём или температура — остаются неизменными. Так, неизменному давлению соответствует изобарный процесс, объёму — изохорный, температуре — изотермический, энтропии — изоэнтропийный (например, обратимый адиабатический процесс). Линии, изображающие данные процессы на какой-либо термодинамической диаграмме, называются изобара, изохора, изотерма и адиабата соответственно. Изопроцессы являются частными случаями политропного процесса.
Адиабати́ческий, или адиаба́тный проце́сс (от др.-греч. ἀδιάβατος — «непроходимый») — термодинамический процесс в макроскопической системе, при котором система не обменивается тепловой энергией с окружающим пространством . Серьёзное исследование адиабатических процессов началось в XVIII веке.Адиабатический процесс является частным случаем политропного процесса, так как при нём теплоёмкость газа равна нулю и, следовательно, постоянна[2]. Адиабатические процессы обратимы только тогда, когда в каждый момент времени система остаётся равновесной (например, изменение состояния происходит достаточно медленно) и изменения энтропии не происходит. Некоторые авторы (в частности, Л. Д. Ландау) называли адиабатическими только квазистатические адиабатические процессы.Адиабатический процесс для идеального газа описывается уравнением Пуассона. Линия, изображающая адиабатный процесс на термодинамической диаграмме, называется адиабатой. Адиабатическими можно считать процессы в целом ряде явлений природы. Так же такие процессы получили ряд применений в технике. Физический смысл адиабатического процесса. Физический смысл адиабатического процесса.Если термодинамический процесс в общем случае являет собой три процесса — теплообмен, совершение системой (или над системой) работы и изменение её внутренней энергии[5], то адиабатический процесс в силу отсутствия теплообмена  системы со средой сводится только к последним двум процессам. Поэтому, первое начало термодинамики в этом случае приобретает вид системы со средой сводится только к последним двум процессам. Поэтому, первое начало термодинамики в этом случае приобретает вид  где где  — изменение внутренней энергии тела, — — изменение внутренней энергии тела, —  работа, совершаемая системой. Изменения энтропии S системы в обратимом адиабатическом процессе вследствие передачи тепла через границы системы не происходит работа, совершаемая системой. Изменения энтропии S системы в обратимом адиабатическом процессе вследствие передачи тепла через границы системы не происходит 
0 здесь т — температура системы, — 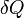 теплота, полученная системой. Благодаря этому адиабатический процесс может быть составной частью обратимого цикла. Политропный процесс, политропический процесс — термодинамический процесс, во время которого удельная теплоёмкость газа остаётся неизменной. В соответствии с сущностью понятия теплоёмкости теплота, полученная системой. Благодаря этому адиабатический процесс может быть составной частью обратимого цикла. Политропный процесс, политропический процесс — термодинамический процесс, во время которого удельная теплоёмкость газа остаётся неизменной. В соответствии с сущностью понятия теплоёмкости  предельными частными явлениями политропного процесса являются изотермический процесс предельными частными явлениями политропного процесса являются изотермический процесс  и адиабатный процесс и адиабатный процесс  В случае идеального газа, изобарный процесс и изохорный процесс также являются политропными. Показатель политропы . Кривая на термодинамических диаграммах, изображающая политропный процесс, называется «политропа». Для идеального газа уравнение политропы может быть записано в виде: В случае идеального газа, изобарный процесс и изохорный процесс также являются политропными. Показатель политропы . Кривая на термодинамических диаграммах, изображающая политропный процесс, называется «политропа». Для идеального газа уравнение политропы может быть записано в виде: 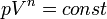 где р — давление, V — объем газа, n — «показатель политропы где р — давление, V — объем газа, n — «показатель политропы  Здесь Здесь  и и  — теплоёмкость газа в данном процессе, и — теплоемкости того же газа, соответственно, при постоянном давлении и объеме . В зависимости от вида процесса, можно определить значение n:Изотермический процесс: . — теплоёмкость газа в данном процессе, и — теплоемкости того же газа, соответственно, при постоянном давлении и объеме . В зависимости от вида процесса, можно определить значение n:Изотермический процесс: .  так как так как  значит, по закону Бойля — Мариотта значит, по закону Бойля — Мариотта  и уравнение политропы вынуждено выглядеть так и уравнение политропы вынуждено выглядеть так  Изобарный процесс Изобарный процесс  так как так как  и уравнение политропы вынуждено выглядеть так: и уравнение политропы вынуждено выглядеть так:  Изохорный процесс Изохорный процесс  так как так как  в процессе в процессе 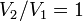 из уравнения политропы следует, что из уравнения политропы следует, что  то есть, что то есть, что   , а это возможно, только если является бесконечным. , а это возможно, только если является бесконечным.
Вопрос 39
Круговым процессом (или циклом) называется процесс, при котором система, проходя через ряд состояний, возвращается в первоначальное. На диаграмме цикл изображается замкнутой кривой (рис. 1). Цикл, который совершает идеальный газ, можно разбить на процессы расширения (1—2) и сжатия (2—1) газа. Работа расширения (равна площади фигуры 1a2V2V11) положительна (dV>0), работа сжатия (равна площади фигуры 2b1V1V22) отрицательна (dV<0). Следовательно, работа, которую совершает газ за цикл, равен площади, охватываемой замкнутой кривой. Если за цикл совершается положительная работа A=∫pdV>0 (цикл идет по часовой стрелке), то он называется прямым (рис. 1, а), если за цикл осуществляется отрицательная работа A=∫pdV<0 (цикл идет против часовой стрелки), то он называется обратным (рис. 1, б).  Прямой цикл применяется в тепловых двигателях — периодически действующих двигателях, которые совершают работу за счет полученной извне теплоты. Обратный цикл применяется в холодильных машинах — периодически действующих установках, в которых за счет работы внешних сил теплота переходит к телу с более высокой температурой. Прямой цикл применяется в тепловых двигателях — периодически действующих двигателях, которые совершают работу за счет полученной извне теплоты. Обратный цикл применяется в холодильных машинах — периодически действующих установках, в которых за счет работы внешних сил теплота переходит к телу с более высокой температурой.
В результате кругового процесса система возвращается в исходное состояние и, значит, полное изменение внутренней энергии газа есть нуль. Поэтому первое начало термодинамики для кругового процесса  т. е. работа, которая совершается за цикл, равна количеству теплоты, полученной извне. Однако в результате кругового процесса система может теплоту как получать, так и отдавать, поэтому т. е. работа, которая совершается за цикл, равна количеству теплоты, полученной извне. Однако в результате кругового процесса система может теплоту как получать, так и отдавать, поэтому  где Q1 — количество теплоты, которая получила система, Q2 — количество теплоты, которое отдала система. Поэтому термический коэффициент полезного действия для кругового процесса где Q1 — количество теплоты, которая получила система, Q2 — количество теплоты, которое отдала система. Поэтому термический коэффициент полезного действия для кругового процесса  Термодинамический процесс называется обратимым, если он может осуществляться как в прямом, так и в обратном направлении, причем если такой процесс осуществляется сначала в прямом, а затем в обратном направлении и система возвращается в первоначальное состояние, то в окружающей среда и в этой системе не происходит никаких изменений. Всякий процесс, не удовлетворяющий этим условиям, является необратимым. Любой равновесный процесс является обратимым. Обратимость равновесного процесса, который происходит в системе, следует из того, что любое промежуточное состояние является состоянием термодинамического равновесия; для него не имеет значения, идет процесс в прямом или обратном направлении. Реальные процессы также сопровождаются диссипацией энергии (из-за трения, теплопроводности и т. д.), которая здесь нами не обсуждается. Обратимые процессы — это идеализация реальных процессов. Их исследование важно по двум причинам: 1) многие процессы в природе и технике практически обратимы; 2) обратимые процессы являются наиболее экономичными; имеют максимальный термический коэффициент полезного действия (КПД), что позволяет указать пути повышения КПД реальных тепловых двигателей. Энтропи́я (от др.-греч. ἐντροπία - поворот, превращение) — в естественных науках мера беспорядка системы, состоящей из многих элементов. В частности, в статистической физике — мера вероятности осуществления какого-либо макроскопического состояния; в теории информации — мера неопределённости какого-либо опыта (испытания), который может иметь разные исходы, а значит, и количество информации; в исторической науке, для экспликации феномена альтернативности истории (инвариантности и вариативности исторического процесса).Энтропия в информатике — степень неполноты, неопределённости знаний.Понятие энтропии впервые было введено Клаузиусом в термодинамике в 1865 году для определения меры необратимого рассеивания энергии, меры отклонения реального процесса от идеального. Определённая как сумма приведённых теплот, она является функцией состояния и остаётся постоянной при обратимых процессах, тогда как в необратимых — её изменение всегда положительно. Термодинамический процесс называется обратимым, если он может осуществляться как в прямом, так и в обратном направлении, причем если такой процесс осуществляется сначала в прямом, а затем в обратном направлении и система возвращается в первоначальное состояние, то в окружающей среда и в этой системе не происходит никаких изменений. Всякий процесс, не удовлетворяющий этим условиям, является необратимым. Любой равновесный процесс является обратимым. Обратимость равновесного процесса, который происходит в системе, следует из того, что любое промежуточное состояние является состоянием термодинамического равновесия; для него не имеет значения, идет процесс в прямом или обратном направлении. Реальные процессы также сопровождаются диссипацией энергии (из-за трения, теплопроводности и т. д.), которая здесь нами не обсуждается. Обратимые процессы — это идеализация реальных процессов. Их исследование важно по двум причинам: 1) многие процессы в природе и технике практически обратимы; 2) обратимые процессы являются наиболее экономичными; имеют максимальный термический коэффициент полезного действия (КПД), что позволяет указать пути повышения КПД реальных тепловых двигателей. Энтропи́я (от др.-греч. ἐντροπία - поворот, превращение) — в естественных науках мера беспорядка системы, состоящей из многих элементов. В частности, в статистической физике — мера вероятности осуществления какого-либо макроскопического состояния; в теории информации — мера неопределённости какого-либо опыта (испытания), который может иметь разные исходы, а значит, и количество информации; в исторической науке, для экспликации феномена альтернативности истории (инвариантности и вариативности исторического процесса).Энтропия в информатике — степень неполноты, неопределённости знаний.Понятие энтропии впервые было введено Клаузиусом в термодинамике в 1865 году для определения меры необратимого рассеивания энергии, меры отклонения реального процесса от идеального. Определённая как сумма приведённых теплот, она является функцией состояния и остаётся постоянной при обратимых процессах, тогда как в необратимых — её изменение всегда положительно.  где Q — приращение энтропии; где Q — приращение энтропии;  — минимальная теплота, подведенная к системе; T — абсолютная температура процеса Употребление в различных дисциплинахТермодинамическая энтропия — термодинамическая функция, характеризующая меру неупорядоченности термодинамической системы, то есть неоднородность расположения и движения её частиц.Информационная энтропия — мера неопределённости источника сообщений, определяемая вероятностями появления тех или иных символов при их передаче.Дифференциальная энтропия — энтропия для непрерывных распределений Энтропия динамической системы — в теории динамических систем мера хаотичности в поведении траекторий системы.Энтропия отражения — часть информации о дискретной системе, которая не воспроизводится при отражении системы через совокупность своих частей.Энтропия в теории управления — мера неопределённости состояния или поведения системы в данных условиях.Энтропия — функция состояния системы, равная в равновесном процессе количеству теплоты, сообщённой системе или отведённой от системы, отнесённому к термодинамической температуре системы.Энтропия — функция, устанавливающая связь между макро- и микро- состояниями; единственная функция в физике, которая показывает направленность процессов. Энтропия — функция состояния системы, которая не зависит от перехода из одного состояния в другое, а зависит только от начального и конечного положения системы. Второе начало термодинамики — физический принцип, накладывающий ограничение на направление процессов передачи тепла между телами.Второе начало термодинамики гласит, что невозможен самопроизвольный переход тепла от тела, менее нагретого, к телу, более нагретому.Второеначало термодинамики запрещает так называемые вечные двигатели второго рода, показывая что коэффициентполезного действия не может равняться единице, поскольку для кругового процесса температура холодильника не может равняться абсолютному нулю.Второе начало термодинамики является постулатом, не доказываемым в рамках термодинамики. Оно было создано на основе обобщения опытных фактов и получило многочисленные экспериментальные подтверждения. Цикл Карно́ — идеальный термодинамический цикл. Тепловая машина Карно, работающая по этому циклу, обладает максимальным КПД из всех машин, у которых максимальная и минимальная температуры осуществляемого цикла совпадают соответственно с максимальной и минимальной температурами цикла Карно. Состоит из 2 адиабатических и 2 изотермических процессов.цикл Карно назван в честь французского военного инженера Сади Карно, который впервые его исследовал в 1824 году.Одним из важных свойств цикла Карно является его обратимость: он может быть проведён как в прямом, так и в обратном направлении, при этом энтропия адиабатически изолированной (без теплообмена с окружающей средой) системы не меняется. Описание цикла Карно Пусть тепловая машина состоит из нагревателя с температурой — минимальная теплота, подведенная к системе; T — абсолютная температура процеса Употребление в различных дисциплинахТермодинамическая энтропия — термодинамическая функция, характеризующая меру неупорядоченности термодинамической системы, то есть неоднородность расположения и движения её частиц.Информационная энтропия — мера неопределённости источника сообщений, определяемая вероятностями появления тех или иных символов при их передаче.Дифференциальная энтропия — энтропия для непрерывных распределений Энтропия динамической системы — в теории динамических систем мера хаотичности в поведении траекторий системы.Энтропия отражения — часть информации о дискретной системе, которая не воспроизводится при отражении системы через совокупность своих частей.Энтропия в теории управления — мера неопределённости состояния или поведения системы в данных условиях.Энтропия — функция состояния системы, равная в равновесном процессе количеству теплоты, сообщённой системе или отведённой от системы, отнесённому к термодинамической температуре системы.Энтропия — функция, устанавливающая связь между макро- и микро- состояниями; единственная функция в физике, которая показывает направленность процессов. Энтропия — функция состояния системы, которая не зависит от перехода из одного состояния в другое, а зависит только от начального и конечного положения системы. Второе начало термодинамики — физический принцип, накладывающий ограничение на направление процессов передачи тепла между телами.Второе начало термодинамики гласит, что невозможен самопроизвольный переход тепла от тела, менее нагретого, к телу, более нагретому.Второеначало термодинамики запрещает так называемые вечные двигатели второго рода, показывая что коэффициентполезного действия не может равняться единице, поскольку для кругового процесса температура холодильника не может равняться абсолютному нулю.Второе начало термодинамики является постулатом, не доказываемым в рамках термодинамики. Оно было создано на основе обобщения опытных фактов и получило многочисленные экспериментальные подтверждения. Цикл Карно́ — идеальный термодинамический цикл. Тепловая машина Карно, работающая по этому циклу, обладает максимальным КПД из всех машин, у которых максимальная и минимальная температуры осуществляемого цикла совпадают соответственно с максимальной и минимальной температурами цикла Карно. Состоит из 2 адиабатических и 2 изотермических процессов.цикл Карно назван в честь французского военного инженера Сади Карно, который впервые его исследовал в 1824 году.Одним из важных свойств цикла Карно является его обратимость: он может быть проведён как в прямом, так и в обратном направлении, при этом энтропия адиабатически изолированной (без теплообмена с окружающей средой) системы не меняется. Описание цикла Карно Пусть тепловая машина состоит из нагревателя с температурой  , холодильника с температурой и , холодильника с температурой и  рабочего тела.Цикл Карно состоит из четырёх стадий: рабочего тела.Цикл Карно состоит из четырёх стадий:
Изотермическое расширение (на рисунке — процесс A→Б). В начале процесса рабочее тело имеет температуру , то есть температуру нагревателя. Затем тело приводится в контакт с нагревателем, который изотермически (при постоянной температуре) передаёт ему количество теплоты . При этом объём рабочего тела увеличивается.
Адиабатическое (изоэнтропическое) расширение (на рисунке — процесс Б→В). Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом его температура уменьшается до температуры холодильника.
Изотермическое сжатие (на рисунке — процесс В→Г). Рабочее тело, имеющее к тому времени температуру , приводится в контакт с холодильником и начинает изотермически сжиматься, отдавая холодильнику количество теплоты .
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


 .
. – амплитуда в точке с координатой x = 0; t – время, за которое волна распространилась на расстояние, равное x; β – коэффициент затухания колебаний;
– амплитуда в точке с координатой x = 0; t – время, за которое волна распространилась на расстояние, равное x; β – коэффициент затухания колебаний;  коэффициент поглощения, зависящий от химической природы среды и от длины волны проходящего света.
коэффициент поглощения, зависящий от химической природы среды и от длины волны проходящего света. ,
, – интенсивность волны на входе в среду.
– интенсивность волны на входе в среду. ,
,  . Следовательно, коэффициент поглощения – физическая величина, численно равная обратному значению толщины слоя вещества, в котором интенсивность волны убывает в е = 2,72 раз.
. Следовательно, коэффициент поглощения – физическая величина, численно равная обратному значению толщины слоя вещества, в котором интенсивность волны убывает в е = 2,72 раз.
 м) наблюдаются резкие максимумы (так называемый линейчатый спектр поглощения). Эти линии соответствуют частотам собственных колебаний электронов в атомах. Спектр поглощения молекул, определяемый колебаниями атомов в молекулах, характеризуется полосами поглощения (примерно
м) наблюдаются резкие максимумы (так называемый линейчатый спектр поглощения). Эти линии соответствуют частотам собственных колебаний электронов в атомах. Спектр поглощения молекул, определяемый колебаниями атомов в молекулах, характеризуется полосами поглощения (примерно  м).
м). ), однако у них наблюдается селективное поглощение света в определенных интервалах длин волн, когда α резко возрастает и наблюдаются сравнительно широкие полосы поглощения (примерно
), однако у них наблюдается селективное поглощение света в определенных интервалах длин волн, когда α резко возрастает и наблюдаются сравнительно широкие полосы поглощения (примерно  м), т.е. диэлектрики имеют сплошной спектр поглощения. Это связано с тем, что в диэлектриках нет свободных электронов и поглощение света обусловлено явлением резонанса при вынужденных колебаниях электронов в атомах и атомов в молекулах диэлектрика.
м), т.е. диэлектрики имеют сплошной спектр поглощения. Это связано с тем, что в диэлектриках нет свободных электронов и поглощение света обусловлено явлением резонанса при вынужденных колебаниях электронов в атомах и атомов в молекулах диэлектрика. ), и поэтому металлы практически непрозрачны для света. В металлах из-за наличия свободных электронов, движущихся под действием электрического поля световой волны, возникают быстропеременные токи, сопровождающиеся выделением джоулевой теплоты. Поэтому энергия световой волны быстро уменьшается, превращаясь во внутреннюю энергию металла. Чем выше проводимость металла, тем сильнее в нем поглощение света.
), и поэтому металлы практически непрозрачны для света. В металлах из-за наличия свободных электронов, движущихся под действием электрического поля световой волны, возникают быстропеременные токи, сопровождающиеся выделением джоулевой теплоты. Поэтому энергия световой волны быстро уменьшается, превращаясь во внутреннюю энергию металла. Чем выше проводимость металла, тем сильнее в нем поглощение света.

 Это объясняется тем, что в газе, находящемся в состоянии равновесия, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям, которое подчиняется вполне определенному статистическому закону. Этот закон теоретически выведен Дж. Максвеллом.При выводе закона распределения молекул по скоростям Максвелл предполагал, что газ состоит из очень большого числа N тождественных молекул, находящихся в состоянии беспорядочного теплового движения при одинаковой температуре. Предполагалось также, что силовые поля на газ не действуют.Закон Максвелла описывается некоторой функцией f(v), называемой функцией распределения молекул по скоростям. Если разбить диапазон скоростей молекул на малые интервалы, равные dv, то на каждый интервал скорости будет приходиться некоторое число молекул dN(v), имеющих скорость, заключенную в этом интервале. Функция f(v) определяет относительное число молекул dN(v)/N, скорости которых лежат в интервале от v до v+dv, т. е.
Это объясняется тем, что в газе, находящемся в состоянии равновесия, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям, которое подчиняется вполне определенному статистическому закону. Этот закон теоретически выведен Дж. Максвеллом.При выводе закона распределения молекул по скоростям Максвелл предполагал, что газ состоит из очень большого числа N тождественных молекул, находящихся в состоянии беспорядочного теплового движения при одинаковой температуре. Предполагалось также, что силовые поля на газ не действуют.Закон Максвелла описывается некоторой функцией f(v), называемой функцией распределения молекул по скоростям. Если разбить диапазон скоростей молекул на малые интервалы, равные dv, то на каждый интервал скорости будет приходиться некоторое число молекул dN(v), имеющих скорость, заключенную в этом интервале. Функция f(v) определяет относительное число молекул dN(v)/N, скорости которых лежат в интервале от v до v+dv, т. е. 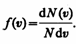 Применяя методы теории вероятностей. Максвелл нашел функцию f(v) — закон о распределеня молекул идеального газа по скоростям:
Применяя методы теории вероятностей. Максвелл нашел функцию f(v) — закон о распределеня молекул идеального газа по скоростям:  Относительное число молекул dN(v)/N, скорости которых лежат в интервале от v до v+dv, находится как площадь заштрихованной полоски на рис. 65. Площадь, ограниченная кривой распределения и осью абсцисс, равна единице. Это означает, что функция f(v) удовлетворяет условию нормировки
Относительное число молекул dN(v)/N, скорости которых лежат в интервале от v до v+dv, находится как площадь заштрихованной полоски на рис. 65. Площадь, ограниченная кривой распределения и осью абсцисс, равна единице. Это означает, что функция f(v) удовлетворяет условию нормировки  Скорость, при которой функция распределения молекул идеального газа по скоростям максимальна, называется наиболее вероятной скоростью. Значение наиболее вероятной скорости можно найти продифференцировав выражение (44.1) (постоянные множители опускаем) по аргументу v, приравняв результат нулю и используя условие для максимума выражения f(v): Значения v=0 и v=¥ соответствуют минимумам выражения .
Скорость, при которой функция распределения молекул идеального газа по скоростям максимальна, называется наиболее вероятной скоростью. Значение наиболее вероятной скорости можно найти продифференцировав выражение (44.1) (постоянные множители опускаем) по аргументу v, приравняв результат нулю и используя условие для максимума выражения f(v): Значения v=0 и v=¥ соответствуют минимумам выражения .  Средняя скорость молекулы <v> (средняя арифметическая скорость) определяется по формуле
Средняя скорость молекулы <v> (средняя арифметическая скорость) определяется по формуле  Подставляя сюда f(v) и интегрируя, получаем
Подставляя сюда f(v) и интегрируя, получаем  Скорости, характеризующие состояние газа: 1) наиболее вероятная
Скорости, характеризующие состояние газа: 1) наиболее вероятная  2) средняя
2) средняя  3) средняя квадратичная
3) средняя квадратичная 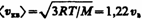 . Исходя из распределения молекул по скоростям
. Исходя из распределения молекул по скоростям  можно найти распределение молекул газа по значениям кинетической энергии e. Для этого перейдем от переменной v к переменной e=m0v2/2. Подставив в v=
можно найти распределение молекул газа по значениям кинетической энергии e. Для этого перейдем от переменной v к переменной e=m0v2/2. Подставив в v=  и dv=
и dv=  de
de  где dN(e) — число молекул, имеющих кинетическую энергию поступательного движения, заключенную в интервале от e до e + de. Таким образом, функция распределения молекул по энергиям теплового движения
где dN(e) — число молекул, имеющих кинетическую энергию поступательного движения, заключенную в интервале от e до e + de. Таким образом, функция распределения молекул по энергиям теплового движения 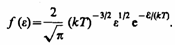 Средняя кинетическая энергия <e> молекулы идеального газа
Средняя кинетическая энергия <e> молекулы идеального газа 

 В статистической физике выводится закон Больцмана о равномерном распределении энергии по степеням свободы молекул: для статистической системы, которая находится в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная kT/2, а на каждую колебательную степень свободы — в среднем энергия, равная kT. Колебательная степень обладает вдвое большей энергией, т.к. на нее приходится как кинетическая энергия (как в случае поступательного и вращательного движений), так и потенциальная, причем средние значения потенциальной и кинетической и энергии одинаковы. Значит, средняя энергия молекул.
В статистической физике выводится закон Больцмана о равномерном распределении энергии по степеням свободы молекул: для статистической системы, которая находится в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная kT/2, а на каждую колебательную степень свободы — в среднем энергия, равная kT. Колебательная степень обладает вдвое большей энергией, т.к. на нее приходится как кинетическая энергия (как в случае поступательного и вращательного движений), так и потенциальная, причем средние значения потенциальной и кинетической и энергии одинаковы. Значит, средняя энергия молекул.  где i — сумма числа поступательных, числа вращательных в удвоенного числа колебательных степеней свободы молекулы: i=iпост+iвращ+2iколеб В классической теории рассматривают молекулы с жесткой связью между атомами; для них i совпадает с числом степеней свободы молекулы.
где i — сумма числа поступательных, числа вращательных в удвоенного числа колебательных степеней свободы молекулы: i=iпост+iвращ+2iколеб В классической теории рассматривают молекулы с жесткой связью между атомами; для них i совпадает с числом степеней свободы молекулы.  Так как в идеальном газе взаимная потенциальная энергия взаимодействия молекул равна нулю (молекулы между собой не взаимодействуют), то внутренняя энергия для одного моля газа, будет равна сумме кинетических энергий NA молекул: Внутренняя энергия для произвольной массы m газ
Так как в идеальном газе взаимная потенциальная энергия взаимодействия молекул равна нулю (молекулы между собой не взаимодействуют), то внутренняя энергия для одного моля газа, будет равна сумме кинетических энергий NA молекул: Внутренняя энергия для произвольной массы m газ  а . где М — молярная масса, ν — количество вещества.
а . где М — молярная масса, ν — количество вещества. Изменение внутренней энергии системы при переходе её из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе, то есть, оно зависит только от начального и конечного состояния системы и не зависит от способа, которым осуществляется этот переход. Это определение особенно важно для химической термодинамики[2] (ввиду сложности рассматриваемых процессов). Иными словами, внутренняя энергия является функцией состояния. В циклическом процессе внутренняя энергия не изменяется.
Изменение внутренней энергии системы при переходе её из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе, то есть, оно зависит только от начального и конечного состояния системы и не зависит от способа, которым осуществляется этот переход. Это определение особенно важно для химической термодинамики[2] (ввиду сложности рассматриваемых процессов). Иными словами, внутренняя энергия является функцией состояния. В циклическом процессе внутренняя энергия не изменяется.  Для элементарного количества теплоты
Для элементарного количества теплоты  элементарной работы
элементарной работы  и малого приращения
и малого приращения  внутренней энергии первый закон термодинамики имеет вид
внутренней энергии первый закон термодинамики имеет вид  Разделение работы на две части, одна из которых описывает работу, совершённую над системой, а вторая — работу, совершённую самой системой, подчёркивает, что эти работы могут быть совершены силами
Разделение работы на две части, одна из которых описывает работу, совершённую над системой, а вторая — работу, совершённую самой системой, подчёркивает, что эти работы могут быть совершены силами  являются полными дифференциалами, а
являются полными дифференциалами, а  Единица измерения теплоёмкости в системе СИ — Дж/К. Удельная теплоёмкость Удельной теплоёмкостью называется теплоёмкость, отнесённая к единичному количеству вещества. Количество вещества может быть измерено в килограммах, кубических метрах и молях. В зависимости от того, к какой количественной единице относится теплоёмкость, различают массовую, объёмную и молярную теплоёмкость.Массовая теплоёмкость (С) — это количество теплоты, которое необходимо подвести к единице массы вещества, чтобы нагреть его на единицу температуры. В СИ измеряется в джоулях на килограмм на кельвин (Дж·кг−1·К−1).Объёмная теплоёмкость (С′) — это количество теплоты, которое необходимо подвести к единице объёма вещества, чтобы нагреть его на единицу температуры. В СИ измеряется в джоулях на кубический метр на кельвин (Дж·м−3·К−1).Молярная теплоёмкость (Сμ) — это количество теплоты, которое необходимо подвести к 1 молю вещества, чтобы нагреть его на единицу температуры. В СИ измеряется в джоулях на моль на кельвин (Дж/(моль·К)). Теплоёмкость для различных состояний вещества Понятие теплоёмкости определено как для веществ в различных агрегатных состояниях (твёрдых тел, жидкостей, газов), так и для ансамблей частиц и квазичастиц (в физике металлов, например, говорят о теплоёмкости электронного газа).Для примера, в молекулярно-кинетической теории газов показывается, что молярная теплоёмкость идеального газа с i степенями свободы при постоянном объёме (для одного моля идеального газа) равна:
Единица измерения теплоёмкости в системе СИ — Дж/К. Удельная теплоёмкость Удельной теплоёмкостью называется теплоёмкость, отнесённая к единичному количеству вещества. Количество вещества может быть измерено в килограммах, кубических метрах и молях. В зависимости от того, к какой количественной единице относится теплоёмкость, различают массовую, объёмную и молярную теплоёмкость.Массовая теплоёмкость (С) — это количество теплоты, которое необходимо подвести к единице массы вещества, чтобы нагреть его на единицу температуры. В СИ измеряется в джоулях на килограмм на кельвин (Дж·кг−1·К−1).Объёмная теплоёмкость (С′) — это количество теплоты, которое необходимо подвести к единице объёма вещества, чтобы нагреть его на единицу температуры. В СИ измеряется в джоулях на кубический метр на кельвин (Дж·м−3·К−1).Молярная теплоёмкость (Сμ) — это количество теплоты, которое необходимо подвести к 1 молю вещества, чтобы нагреть его на единицу температуры. В СИ измеряется в джоулях на моль на кельвин (Дж/(моль·К)). Теплоёмкость для различных состояний вещества Понятие теплоёмкости определено как для веществ в различных агрегатных состояниях (твёрдых тел, жидкостей, газов), так и для ансамблей частиц и квазичастиц (в физике металлов, например, говорят о теплоёмкости электронного газа).Для примера, в молекулярно-кинетической теории газов показывается, что молярная теплоёмкость идеального газа с i степенями свободы при постоянном объёме (для одного моля идеального газа) равна: 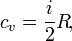 где R ≈ 8,31 Дж/(моль·К) — универсальная газовая постоянная. А при постоянном давлении
где R ≈ 8,31 Дж/(моль·К) — универсальная газовая постоянная. А при постоянном давлении  Удельные теплоёмкости многих веществ приведены в справочниках обычно для процесса при постоянном давлении. К примеру, удельная теплоёмкость жидкой воды при нормальных условиях — 4200 Дж/(кг·К); льда — 2100 Дж/(кг·К). Теория теплоёмкости Сравнение моделей Дебая и Эйнштейна для теплоёмкости твёрдого тела Существует несколько теорий теплоёмкости твердого тела:Закон Дюлонга — Пти и закон Джоуля — Коппа. Оба закона выведены из классических представлений и с определенной точностью справедливы лишь для нормальных температур (примерно от 15 °C до 100 °C).Квантовая теория теплоёмкостей Эйнштейна. Первое применение квантовых законов к описанию теплоёмкости.Квантовая теория теплоёмкостей Дебая. Содержит наиболее полное описание и хорошо согласуется с экспериментом.Теплоёмкость системы невзаимодействующих частиц (например, газа) определяется числом степеней свободы частиц.
Удельные теплоёмкости многих веществ приведены в справочниках обычно для процесса при постоянном давлении. К примеру, удельная теплоёмкость жидкой воды при нормальных условиях — 4200 Дж/(кг·К); льда — 2100 Дж/(кг·К). Теория теплоёмкости Сравнение моделей Дебая и Эйнштейна для теплоёмкости твёрдого тела Существует несколько теорий теплоёмкости твердого тела:Закон Дюлонга — Пти и закон Джоуля — Коппа. Оба закона выведены из классических представлений и с определенной точностью справедливы лишь для нормальных температур (примерно от 15 °C до 100 °C).Квантовая теория теплоёмкостей Эйнштейна. Первое применение квантовых законов к описанию теплоёмкости.Квантовая теория теплоёмкостей Дебая. Содержит наиболее полное описание и хорошо согласуется с экспериментом.Теплоёмкость системы невзаимодействующих частиц (например, газа) определяется числом степеней свободы частиц. системы со средой сводится только к последним двум процессам. Поэтому, первое начало термодинамики в этом случае приобретает вид
системы со средой сводится только к последним двум процессам. Поэтому, первое начало термодинамики в этом случае приобретает вид  где
где  — изменение внутренней энергии тела, —
— изменение внутренней энергии тела, —  работа, совершаемая системой. Изменения энтропии S системы в обратимом адиабатическом процессе вследствие передачи тепла через границы системы не происходит
работа, совершаемая системой. Изменения энтропии S системы в обратимом адиабатическом процессе вследствие передачи тепла через границы системы не происходит 
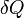 теплота, полученная системой. Благодаря этому адиабатический процесс может быть составной частью обратимого цикла. Политропный процесс, политропический процесс — термодинамический процесс, во время которого удельная теплоёмкость газа остаётся неизменной. В соответствии с сущностью понятия теплоёмкости
теплота, полученная системой. Благодаря этому адиабатический процесс может быть составной частью обратимого цикла. Политропный процесс, политропический процесс — термодинамический процесс, во время которого удельная теплоёмкость газа остаётся неизменной. В соответствии с сущностью понятия теплоёмкости  предельными частными явлениями политропного процесса являются изотермический процесс
предельными частными явлениями политропного процесса являются изотермический процесс  и адиабатный процесс
и адиабатный процесс  В случае идеального газа, изобарный процесс и изохорный процесс также являются политропными. Показатель политропы . Кривая на термодинамических диаграммах, изображающая политропный процесс, называется «политропа». Для идеального газа уравнение политропы может быть записано в виде:
В случае идеального газа, изобарный процесс и изохорный процесс также являются политропными. Показатель политропы . Кривая на термодинамических диаграммах, изображающая политропный процесс, называется «политропа». Для идеального газа уравнение политропы может быть записано в виде: 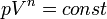 где р — давление, V — объем газа, n — «показатель политропы
где р — давление, V — объем газа, n — «показатель политропы  Здесь
Здесь  и
и  — теплоёмкость газа в данном процессе, и — теплоемкости того же газа, соответственно, при постоянном давлении и объеме . В зависимости от вида процесса, можно определить значение n:Изотермический процесс: .
— теплоёмкость газа в данном процессе, и — теплоемкости того же газа, соответственно, при постоянном давлении и объеме . В зависимости от вида процесса, можно определить значение n:Изотермический процесс: .  так как
так как  значит, по закону Бойля — Мариотта
значит, по закону Бойля — Мариотта  и уравнение политропы вынуждено выглядеть так
и уравнение политропы вынуждено выглядеть так  Изобарный процесс
Изобарный процесс  так как
так как  и уравнение политропы вынуждено выглядеть так:
и уравнение политропы вынуждено выглядеть так:  Изохорный процесс
Изохорный процесс  так как
так как  в процессе
в процессе 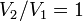 из уравнения политропы следует, что
из уравнения политропы следует, что  то есть, что
то есть, что 
 , а это возможно, только если является бесконечным.
, а это возможно, только если является бесконечным. Прямой цикл применяется в тепловых двигателях — периодически действующих двигателях, которые совершают работу за счет полученной извне теплоты. Обратный цикл применяется в холодильных машинах — периодически действующих установках, в которых за счет работы внешних сил теплота переходит к телу с более высокой температурой.
Прямой цикл применяется в тепловых двигателях — периодически действующих двигателях, которые совершают работу за счет полученной извне теплоты. Обратный цикл применяется в холодильных машинах — периодически действующих установках, в которых за счет работы внешних сил теплота переходит к телу с более высокой температурой. т. е. работа, которая совершается за цикл, равна количеству теплоты, полученной извне. Однако в результате кругового процесса система может теплоту как получать, так и отдавать, поэтому
т. е. работа, которая совершается за цикл, равна количеству теплоты, полученной извне. Однако в результате кругового процесса система может теплоту как получать, так и отдавать, поэтому  где Q1 — количество теплоты, которая получила система, Q2 — количество теплоты, которое отдала система. Поэтому термический коэффициент полезного действия для кругового процесса
где Q1 — количество теплоты, которая получила система, Q2 — количество теплоты, которое отдала система. Поэтому термический коэффициент полезного действия для кругового процесса  Термодинамический процесс называется обратимым, если он может осуществляться как в прямом, так и в обратном направлении, причем если такой процесс осуществляется сначала в прямом, а затем в обратном направлении и система возвращается в первоначальное состояние, то в окружающей среда и в этой системе не происходит никаких изменений. Всякий процесс, не удовлетворяющий этим условиям, является необратимым. Любой равновесный процесс является обратимым. Обратимость равновесного процесса, который происходит в системе, следует из того, что любое промежуточное состояние является состоянием термодинамического равновесия; для него не имеет значения, идет процесс в прямом или обратном направлении. Реальные процессы также сопровождаются диссипацией энергии (из-за трения, теплопроводности и т. д.), которая здесь нами не обсуждается. Обратимые процессы — это идеализация реальных процессов. Их исследование важно по двум причинам: 1) многие процессы в природе и технике практически обратимы; 2) обратимые процессы являются наиболее экономичными; имеют максимальный термический коэффициент полезного действия (КПД), что позволяет указать пути повышения КПД реальных тепловых двигателей. Энтропи́я (от др.-греч. ἐντροπία - поворот, превращение) — в естественных науках мера беспорядка системы, состоящей из многих элементов. В частности, в статистической физике — мера вероятности осуществления какого-либо макроскопического состояния; в теории информации — мера неопределённости какого-либо опыта (испытания), который может иметь разные исходы, а значит, и количество информации; в исторической науке, для экспликации феномена альтернативности истории (инвариантности и вариативности исторического процесса).Энтропия в информатике — степень неполноты, неопределённости знаний.Понятие энтропии впервые было введено Клаузиусом в термодинамике в 1865 году для определения меры необратимого рассеивания энергии, меры отклонения реального процесса от идеального. Определённая как сумма приведённых теплот, она является функцией состояния и остаётся постоянной при обратимых процессах, тогда как в необратимых — её изменение всегда положительно.
Термодинамический процесс называется обратимым, если он может осуществляться как в прямом, так и в обратном направлении, причем если такой процесс осуществляется сначала в прямом, а затем в обратном направлении и система возвращается в первоначальное состояние, то в окружающей среда и в этой системе не происходит никаких изменений. Всякий процесс, не удовлетворяющий этим условиям, является необратимым. Любой равновесный процесс является обратимым. Обратимость равновесного процесса, который происходит в системе, следует из того, что любое промежуточное состояние является состоянием термодинамического равновесия; для него не имеет значения, идет процесс в прямом или обратном направлении. Реальные процессы также сопровождаются диссипацией энергии (из-за трения, теплопроводности и т. д.), которая здесь нами не обсуждается. Обратимые процессы — это идеализация реальных процессов. Их исследование важно по двум причинам: 1) многие процессы в природе и технике практически обратимы; 2) обратимые процессы являются наиболее экономичными; имеют максимальный термический коэффициент полезного действия (КПД), что позволяет указать пути повышения КПД реальных тепловых двигателей. Энтропи́я (от др.-греч. ἐντροπία - поворот, превращение) — в естественных науках мера беспорядка системы, состоящей из многих элементов. В частности, в статистической физике — мера вероятности осуществления какого-либо макроскопического состояния; в теории информации — мера неопределённости какого-либо опыта (испытания), который может иметь разные исходы, а значит, и количество информации; в исторической науке, для экспликации феномена альтернативности истории (инвариантности и вариативности исторического процесса).Энтропия в информатике — степень неполноты, неопределённости знаний.Понятие энтропии впервые было введено Клаузиусом в термодинамике в 1865 году для определения меры необратимого рассеивания энергии, меры отклонения реального процесса от идеального. Определённая как сумма приведённых теплот, она является функцией состояния и остаётся постоянной при обратимых процессах, тогда как в необратимых — её изменение всегда положительно.  где Q — приращение энтропии;
где Q — приращение энтропии;  , холодильника с температурой и
, холодильника с температурой и  рабочего тела.Цикл Карно состоит из четырёх стадий:
рабочего тела.Цикл Карно состоит из четырёх стадий: