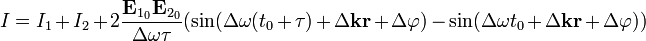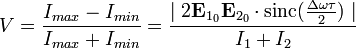|
|
Интерференция света в тонких плёнках
Интерференция в тонкой плёнке. Альфа — угол падения, бета — угол отражения, жёлтый луч отстанет от оранжевого, они сводятся глазом в один и интерферируют. Получить устойчивую интерференционную картину для света от двух разделённых в пространстве и независящих друг от друга источников света не так легко, как для источников волн на воде. Атомы испускают свет цугами очень малой продолжительности, и когерентность нарушается. Сравнительно просто такую картину можно получить, сделав так, чтобы интерферировали волны одного и того же цуга[1]. Так, интерференция возникает при разделении первоначального луча света на два луча при его прохождении через тонкую плёнку, например плёнку, наносимую на поверхность линз у просветлённыхобъективов. Луч света, проходя через плёнку толщиной Лучи соседних участков спектра по обе стороны от
где k=0,1,2... и
Кольца Ньютона Основная статья: Кольца Ньютона
Возникновение колец Ньютона. Волна 2 отстанет от волны 1. Другим методом получения устойчивой интерференционной картины для света служит использование воздушных прослоек, основанное на одинаковой разности хода двух частей волны: одной — сразу отраженной от внутренней поверхности линзы и другой — прошедшей воздушную прослойку под ней и лишь затем отразившейся. Её можно получить, если положить плосковыпуклую линзу на стеклянную пластину выпуклостью вниз. При освещении линзы сверху монохроматическим светом образуется тёмное пятно в месте достаточно плотного соприкосновения линзы и пластинки, окружённое чередующимися тёмными и светлыми концентрическими кольцами разной интенсивности. Тёмные кольца соответствуют интерференционным минимумам, а светлые — максимумам, одновременно тёмные и светлые кольца являются изолиниями равной толщины воздушной прослойки. Измерив радиус светлого или тёмного кольца и определив его порядковый номер от центра, можно определить длину волны монохроматического света. Чем круче поверхность линзы, особенно ближе к краям, тем меньше расстояние между соседними светлыми или тёмными кольцами[2]. Математическое описание Интерференция двух плоских волн Пусть имеются две плоские волны: По принципу суперпозиции результирующее поле в области пересечения этих волн будет определяться суммой:
Интенсивность задается соотношением:
Откуда с учетом:
Для простоты рассмотрим одномерный случай
Интерференционная картина представляет собой чередование светлых и темных полос, шаг которых равен: Примером этого случая является интерференционная картина в отраженном от поверхностей плоскопараллельной пластинки свете. Случай неравных частот В некоторых учебниках и пособиях говорится о том, что интерференция света возможна только для волн образованных от одного источника света путём амплитудного либо полевого деления волновых фронтов. Это утверждение является неверным. С точки зрения принципа суперпозиции интерференция существует всегда, даже когда интерферируют волны от двух разных источников света. Правильно было бы говорить о наблюдении или возможности наблюдения интерференционной картины. Последняя может быть нестационарна во времени, что приводит к замазыванию и исчезновению интерференционных полос. Рассмотрим две плоские волны с разными частотами:
По принципу суперпозиции результирующее поле в области пересечения этих волн будет определяться суммой:
Пусть некоторый прибор, обладающий некоторым характерным временем регистрации (экспозиции), фотографирует интерференционную картину. В физической оптике интенсивностью называют усредненный по времени поток световой энергии через единичную площадку ортогональную направлению распространения волны. Время усреднения определяется временем интегрирования фотоприемника, а для устройств, работающих в режиме накопления сигнала (фотокамеры, фотопленка и т. п.), временем экспозиции. Поэтому приемники излучения оптического диапазона реагируют на среднее значение потока энергии. То есть сигнал с фотоприемника пропорционален:
где под <> подразумевается усреднение. Во многих научно технических приложениях данное понятие обобщается на любые, в том числе и не плоские волны. Так как в большинстве случаев, например в задачах связанных с интерференцией и дифракцией света, исследуется в основном пространственное положение максимумов и минимумов и их относительная интенсивность, постоянные множители, не зависящие от пространственных координат, часто не учитываются. По этой причине часто полагают:
Квадрат модуля амплитуды задается соотношением:
Откуда, подставляя напряженность электрического поля, получим:
С учётом определения интенсивности можно перейти к следующиму выражению: [1] Взятие интеграла по времени и применение формулы разности синусов даёт следующие выражения для распределения интенсивности:
В итоговом соотношении слагаемое, содержащее тригонометрические множители, называется интерференционным членом. Оно отвечает за модуляцию интенсивности интерференционными полосами. Степень различимости полос на фоне средней интенсивности называется видностью или контрастом интерференционных полос:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
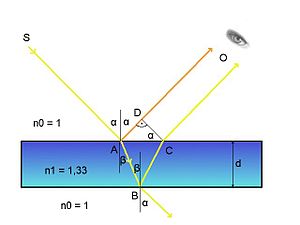

 , отразится дважды — от внутренней и наружной её поверхностей. Отражённые лучи будут иметь постоянную разность фаз, равную удвоенной толщине плёнки, от чего лучи становятся когерентными и будут интерферировать. Полное гашение лучей произойдет при
, отразится дважды — от внутренней и наружной её поверхностей. Отражённые лучи будут иметь постоянную разность фаз, равную удвоенной толщине плёнки, от чего лучи становятся когерентными и будут интерферировать. Полное гашение лучей произойдет при 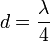 , где
, где 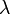 — длина волны. Если
— длина волны. Если  нм, то толщина плёнки равняется 550:4=137,5 нм.
нм, то толщина плёнки равняется 550:4=137,5 нм.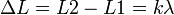 — условие максимума;
— условие максимума;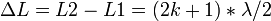 — условие минимума,
— условие минимума, — оптическая длина пути первого и второго луча, соответственно.
— оптическая длина пути первого и второго луча, соответственно.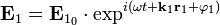 и
и 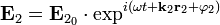
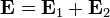
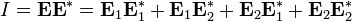
 :
: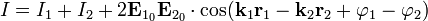
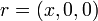 и сонаправленность поляризаций волн,
и сонаправленность поляризаций волн,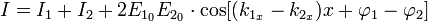
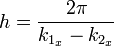
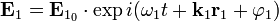 и
и 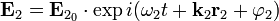


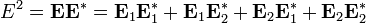
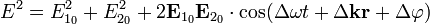 , где
, где 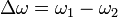 ,
, 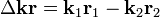 ,
, 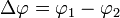
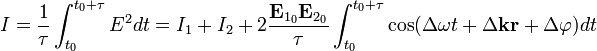 , где
, где