
|
|
Разрешающая способность оптических приборовИспользуя даже идеальную оптическую систему (такую, для которой отсутствуют дефекты и аберрации), невозможно получить стигматическое изображение точечного источника, что объясняется волновой природой света. Изображение любой светящейся точки в монохроматическом свете представляет собой дифракционную картину, т. е. точечный источник отображается в виде центрального светлого пятна, окруженного чередующимися темными и светлыми кольцами. Согласнокритерию Рэлея, изображения двух близлежащих одинаковых точечных источников или двух близлежащих спектральных линий с равными интенсивностями и одинаковыми симметричными контурами разрешимы (разделены для восприятия), если центральный максимум дифракционной картины от одного источника (линии) совпадает с первым минимумом дифракционной картины от другого (рис. 265, а). При выполнении критерия Рэлея интенсивность «провала» между максимумами составляет 80% интенсивности в максимуме, что является достаточным для разрешения линий 1 и 2. Если критерий Рэлея нарушен, то наблюдается одна линия (рис. 265, б).
1. Разрешающая способность объектива. Если на объектив падает свет от двух удаленных точечных источников S1 и S2 (например, звезд) с некоторым угловым расстоянием , то вследствие дифракции световых волн на краях диафрагмы, ограничивающей объектив, в его фокальной плоскости вместо двух точек наблюдаются максимумы, окруженные чередующимися темными и светлыми кольцами (рис. 266).Можно доказать, что две близлежащие звезды, наблюдаемые в объективе в монохроматическом свете, разрешимы, если угловое расстояние между ними
где — длина волны света, D — диаметр объектива. Разрешающей способностью (разрешающей силой) объектива называется величина
где — наименьшее угловое расстояние между двумя точками, при котором они еще оптическим прибором разрешаются. Согласно критерию Рэлея, изображения двух одинаковых точек разрешимы, когда центральный максимум дифракционной картины для одной точки совпадает с первым минимумом дифракционной картины для другой (рис. 266). Из рисунка следует, что при выполнении критерия Рэлея угловое расстояние между точками должно быть равно , т. е. с учетом (183.1)
Следовательно, разрешающая способность объектива
т. е. зависит от его диаметра и длины волны света.
Из формулы (183.2) видно, что для увеличения разрешающей способности оптических приборов нужно либо увеличить диаметр объектива, либо уменьшить длину волны. Поэтому для наблюдения более мелких деталей предмета используют ультрафиолетовое излучение, а полученное изображение в данном случае наблюдается с помощью флуоресцирующего экрана либо фиксируется на фотопластинке. Еще большую разрешающую способность можно было бы получить с помощью рентгеновского излучения, но оно обладает большой проникающей способностью и проходит через вещество не преломляясь; следовательно, в данном случае невозможно создать преломляющие линзы. Потоки электронов (при определенных энергиях) обладают примерно такой же длиной волны, как и рентгеновское излучение. Поэтому электронный микроскоп имеет очень высокую разрешающую способность. Разрешающей способностью спектрального прибора называют безразмерную величину
где — абсолютное значение минимальной разности длин волн двух соседних спектральных линий, при которой эти линии регистрируются раздельно. 2. Разрешающая способность дифракционной решетки.Пусть максимум т-го порядка для длины волны 2 наблюдается под углом , т. е., согласно (180.3), dsin=m2. При переходе от максимума к соседнему минимуму разность хода меняется на /N (см. (180.4)), где N — число щелей решетки. Следовательно,минимум 1, наблюдаемый под углом min, удовлетворяет условию dsinmin=m1+1/N. По критерию Рэлея, =min, т. е. m2=m1+1/N или 2/(2–1)=mN.Tax как 1 и 2 близки между собой, т. е. 2–1= то, согласно (183.3),
Таким образом, разрешающая способность дифракционной решетки пропорциональна порядку m спектра и числу N щелей, т. е. при заданном числе щелей увеличивается при переходе к большим значениям порядка m интерференции. Современные дифракционные решетки обладают довольно высокой разрешающей способностью (до 2105).
Дисперсия Света Как уже говорилось, свет, проходя через трехгранную призму, преломляется и при выходе из призмы отклоняется от своего первоначального направления к основанию призмы. Величина отклонения луча зависит от показателя преломления вещества призмы, и, как показывают опыты, показатель преломления зависит от частоты света. Зависимость показателя преломления вещества от частоты (длины волн) света называется дисперсией.Очень просто наблюдать явление дисперсии при пропускании белого света через призму (рис. 102). При выходе из призмы белый свет разлагается на семь цветов: красный, оранжевый, желтый, зеленый, голубой, синий, фиолетовый. Меньше всех отклоняется красный свет, больше - фиолетовый. Это говорит о том, что стекло имеет для фиолетового света наибольший показатель преломления, а для красного - наименьший. Свет с разными длинами волн распространяется в среде с разными скоростями: фиолетовый с наименьшей, красный - наибольшей, так как n= c/v , В результате прохождения света через прозрачную призму получается упорядоченное расположение монохроматических электромагнитных волн оптического диапазона - спектр. Все спектры делятся на спектры испускания и спектры поглощения. Спектр испускания создается светящимися телами. Если на пути лучей, падающих на призму, поместить холодный, неизлучающий газ, то на фоне непрерывного спектра источника появляются темные линии.
При этом получим спектр поглощения газа. Немецкий физик Г. Кирхгоф (1824-1887) открыл закон, согласно которому спектральный состав света, который излучается телами в горячем состоянии, поглощается ими в холодном состоянии (атомы данного элемента поглощают те длины волн, которые излучают при высокой температуре). Спектры испускания делятся насплошные, линейчатые и полосатые. Сплошной спектр дают раскаленные твердые и жидкие тела. Линейчатый спектр - это совокупность определенных спектральных линий (на черном фоне). Такой спектр дают возбужденные газы, находящиеся в атомарном состоянии. Изолированные атомы данного химического элемента излучают строго определенные длины волн. Полосатый спектр представляет собой отдельные спектральные полосы, разделенные темными промежутками. В отличие от линейчатых спектров полосатые спектры создаются не атомами, а молекулами, не связанными или слабо связанными друг с другом. ЭЛЕКТРОННАЯ ТЕОРИЯ ДИСПЕРСИИ СВЕТА Из макроскопической электромагнитной теории Максвелла следует, что абсолютный показатель преломления среды
где — диэлектрическая проницаемость среды, — магнитная проницаемость. В оптической области спектра для всех веществ 1, поэтому
Из формулы (186.1) выявляются некоторые противоречия с опытом: величина n, являясь переменной, остается в то же время равной определенной постоянной Применим электронную теорию дисперсии света для однородного диэлектрика, предположив формально, что дисперсия света является следствием зависимости от частоты световых волн. Диэлектрическая проницаемость вещества, по определению (см. (88.6) и (88.2)), равна
где { — диэлектрическая восприимчивость среды, 0 — электрическая постоянная, Р — мгновенное значение поляризованности. Следовательно,
т.е. зависит от Р. В данном случае основное значение имеет электронная поляризация, т.е. вынужденные колебания электронов под действием электрической составляющей поля волны, так как для ориентационной поляризации молекул частота колебаний в световой волне очень высока (1015 Гц). В первом приближении можно считать, что вынужденные колебания совершают только внешние, наиболее слабо связанные с ядром электроны —оптические электроны. Для простоты рассмотрим колебания только одного оптического электрона. Наведенный дипольный момент электрона, совершающего вынужденные колебания, равен р=ех, где е — заряд электрона, х — смещение электрона под действием электрического поля световой волны. Если концентрация атомов в диэлектрике равна n0, то мгновенное значение поляризованности
Из (186.2) и (186.3) получим
Следовательно, задача сводится к определению смещения х электрона под действием внешнего поля Е. Поле световой волны будем считать функцией частоты , т. е. изменяющимся по гармоническому закону: Е = Е0cost. Уравнение вынужденных колебаний электрона (см. §147) для простейшего случая (без учета силы сопротивления, обусловливающей поглощение энергии падающей волны) запишется в виде
где F0 = еЕ0 — амплитудное значение силы, действующей на электрон со стороны поля волны,
где
в чем легко убедиться подстановкой (см. (147.8)). Подставляя (186.6) и (186.7) в (186.4), получим
Если в веществе имеются различные заряды еi, совершающие вынужденные колебания с различными собственными частотами 0i, то
где т, — масса i-го заряда. Из выражений (186.8) и (186.9) вытекает, что показатель преломления n зависит от частоты внешнего поля, т. е. полученные зависимости действительно подтверждают явление дисперсии света, хотя и при указанных выше допущениях, которые в дальнейшем надо устранить. Из выражений (186.8) и (186.9) следует, что в области от = 0 до = 0n2 больше единицы и возрастает с увеличением (нормальная дисперсия); при = 0n2 = ±; в области от = 0 до = n2 меньше единицы и возрастает от –до 1 (нормальная дисперсия). Перейдя от n2 к n, получим, что график зависимости nот имеет вид, изображенный на рис. 270. Такое поведение n вблизи 0 — результат допущения об отсутствии сил сопротивления при колебаниях электронов. Если принять в расчет и это обстоятельство, то график функции n() вблизи 0 задастся штриховой линией АВ. Область АВ — область аномальной дисперсии (nубывает при возрастании ), остальные участки зависимости nот описывают нормальную дисперсию (n возрастает с возрастанием ).
Российскому физику Д. С. Рождественскому (1876—1940) принадлежит классическая работа по изучению аномальной дисперсии в парах натрия. Он разработал интерференционный метод для очень точного измерения показателя преломления паров и экспериментально показал, что формула (186.9) правильно характеризует зависимость nот, а также ввел в нее поправку, учитывающую квантовые свойства света и атомов. ДИСПЕРСИЯ ВЕЩЕСТВА 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

 (183.1)
(183.1)

 (183.2)
(183.2)
 (183.3)
(183.3)


 (186.1)
(186.1) . Кроме того, значения n, получаемые из этого выражения, не согласуются с опытными значениями. Трудности объяснения дисперсии света с точки зрения электромагнитной теории Максвелла устраняются электронной теорией Лоренца. В теории Лоренца дисперсия света рассматривается как результат взаимодействия электромагнитных волн с заряженными частицами, входящими в состав вещества и совершающими вынужденные колебания в переменном электромагнитном поле волны.
. Кроме того, значения n, получаемые из этого выражения, не согласуются с опытными значениями. Трудности объяснения дисперсии света с точки зрения электромагнитной теории Максвелла устраняются электронной теорией Лоренца. В теории Лоренца дисперсия света рассматривается как результат взаимодействия электромагнитных волн с заряженными частицами, входящими в состав вещества и совершающими вынужденные колебания в переменном электромагнитном поле волны.
 (186.2)
(186.2)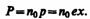 (186.3)
(186.3) (186.4)
(186.4) (186.5)
(186.5) — собственная частота колебаний электрона, т — масса электрона. Решив уравнение (186.5), найдем = n2 в зависимости от констант атома (е, т, 0) и частоты внешнего поля, т.е. решим задачу дисперсии. Решение уравнения (186.5) можно записать в виде
— собственная частота колебаний электрона, т — масса электрона. Решив уравнение (186.5), найдем = n2 в зависимости от констант атома (е, т, 0) и частоты внешнего поля, т.е. решим задачу дисперсии. Решение уравнения (186.5) можно записать в виде (186.6)
(186.6)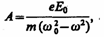 (186.7)
(186.7) (186.8)
(186.8) (186.9)
(186.9)