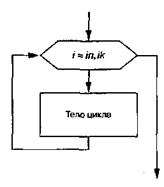
Задачи на циклы с параметром.

Операторы цикла с пред- и постусловием, несмотря на то что обладают значи­тельной гибкостью, не слишком удобны для организации «строгих» циклов, которые должны быть выполнены заданное число раз. Оператор цикла с пара­метром используется именно в таких случаях.

for <параметр_цикла>:=<начальное_знач.> to <конечное_знач.> do

<оператор>;

for <параметр_цикла>:=<конечное_знач.> downto <начальное_знач.> do

<оператор>;

Оператор, представляющий собой тело цикла, может быть простым или составным. Параметр цикла, а также диапазон его изменения могут быть толь­ко целочисленного или перечислимого типа. Параметр описывается совмест­но с другими переменными. Шаг цикла for всегда постоянный и равен интер­валу между двумя ближайшими значениями типа параметра цикла. Например:

var { Описание параметров цикла. }

i: integer; c:char; b: boolean; begin {Вывод на печать целых чисел от 1 до 10.}

for i:=l to 10 do writeln(i);{ Шаг цикла равен 1. }

{ Вывод на печать чисел от 10 до -10, }

for i:=10 downto -10 do { Шаг цикла равен -1. }

writeln(i);

{ Вывод на печать латинских символов от а до r. }

{ Параметр цикла изменяется от а до г в алфавитном порядке. }

for c:='a' to 'r' do writeln(c); end.

Выполнение цикла начинается с присвоения параметру стартового значе­ния. Затем следует проверка, не превосходит ли параметр конечное значение. Если результат проверки утвердительный, то цикл считается завершенным, и управление передается следующему за телом цикла оператору. В противном случае выполняется тело цикла, и параметр меня­ет свое значение на следующее согласно заголов­ку цикла. Далее снова производится проверка значения параметра цикла, и алгоритм повторяется. В блок-схемах такие циклы изображаются так, как показано на рис. 3.2.

Здесь i- переменная цикла, in- начальное зна­чение переменной цикла, ik- конечное значение переменной цикла. Блок, в котором указаны все эти значения, называется блоком модификации. Шаг изменения переменной цикла равен единице. Алго­ритм, изображенный на

рис. работает следующим образом: переменной цикла присваивается начальное значение, затем значение переменной в цикле с параметром цикла увеличивается на единицу, и цикл повторяется. Так продолжается до тех пор, пока переменная цикла не превысит свое конечное значение, после чего цикл заканчивается. Если шаг изменения равен-1, то в блоке модификации мы напишем: i:=in,ik,-1.

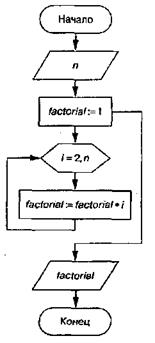
ПРИМЕР 3.10. Вычислить факториал числа N (N!=l*2*3* ...*N). Блок-схема приведена на рис. 3.3.

Входные данные: N - целое число, факториал которого необходимо вычис­лить.

Выходные данные: factorial - значение факториала числа N. Промежуточные данные: i - параметр цикла.

Вводится число N. Переменной factorial присваивается начальное значение. Затем организуется цикл, причем в блок-схеме для этого используется блок модификации. Здесь параметру цикла i присваивается начальное значение 1, и цикл повторяется до N с шагом 1. Когда параметр r становится больше N, цикл заканчивается, и на печать выводится значение переменой factorial, которая была вычислена в теле цикла.

Рис.3.3 т Алгоритм вычисления факториала

Теперь рассмотрим текст программы вычисления факториала на языке Тур­бо Паскаль.

var

factorial, n, i: integer;

begin

write('n=');

readln(n);

factorial:=1,- { Стартовое значение. }

for i:=2 to n do

factorial:=factorial*i;

writeln(factorial);

end.

Алгоритмы

Алгоритм - четкое описание последовательности действий, которые необходи­мо выполнить при решении задачи. Можно сказать, что алгоритм описывает процесс преобразования исходных данных в результаты, так как для решения любой задачи необходимо:

1. Ввести исходные данные.

2. Преобразовать исходные данные в результаты (выходные данные).

3. Вывести результаты.

Разработка алгоритма решения задачи - это разбиение задачи на последова­тельно выполняемые этапы, причем результаты выполнения предыдущих эта­пов могут использоваться в качестве исходных данных для последующих. При этом должны быть четко указаны как содержание каждого этапа, так и порядок их выполнения. Отдельный этап алгоритма представляет собой либо более простую, чем исходная, задачу, алгоритм решения которой известен (разрабо­тан заранее), либо достаточно простую и понятную без пояснений последова­тельность действий.

Приведем примеры алгоритмов из обыденной жизни:

а) поездка в институт;

б) ремонт телевизора (по инструкции);

в) поиск пропавшей вещи;

г) выращивание растений на участке и т.п.

Не все задачи могут быть решены с использованием алгоритмов. Например, написание музыки, написание стихов, научное открытие.

Компьютер используется для решения лишь тех задач, для которых может быть составлен алгоритм.

Любой алгоритм обладает следующими свойствами: детер­минированностью, массовостью, результативностью и дискретностью.

Детерминированность (определенность) означает, что набор ука­заний алгоритма должен быть однозначно и точно понят любым исполнителем. Это свойство определяет однозначность результата работы алгоритма при заданных исходных данных.

Массовость алгоритма предполагает возможность варьирования исходных данных в некоторых пределах. Это свойство определяет пригодность использования алгоритма для решения множества кон­кретных задач определенного класса.

Результативность алгоритма означает, что для любых допусти­мых исходных данных он должен через конечное число шагов (или итераций) завершить свою работу.

Дискретность алгоритма означает возможность разбиения опре­деленного алгоритмического процесса на отдельные элементарные этапы, возможность реализации которых человеком или компьюте­ром не вызывает сомнения, а результат выполнения каждого эле­ментарного этапа вполне определен и понятен.

Таким образом, алгоритм дает возможность чисто механически решать любую конкретную задачу из некоторого класса однотипных задач.

Существует несколько способов описания алго­ритмов: словесный, формально-словесный, графический и др.

Словесный способ описания алгоритма отражает содержание вы­полняемых действий средствами естественного языка. К достоинст­вам этого способа описания следует отнести его общедоступность, а также возможность описывать алгоритм с любой степенью детали­зации. К главным недостаткам этого способа следует отнести доста­точно громоздкое описание, отсутствие строгой формализации в силу неоднозначности восприятия естественного языка.

Формально-словесный способ описания алгоритма основан на за­писи содержания выполняемых действий с использованием изобра­зительных возможностей языка математики, дополненного с целью указания необходимых пояснений средствами естественного языка. Данный способ, обладая всеми достоинствами словесного способа, вместе с тем более лаконичен, а значит, и более нагляден, имеет большую формализацию, однако также не является строго формальным.

Графический способ описания алгоритмов представляет собой изображение логико-математической структуры алгоритма, при котором все этапы процесса обработки данных представляются с помощью определенного набора геометрических фигур (блоков), имеющих строго определенную конфигурацию в соответствии с характером выполняемых действий.

Для облегчения процесса разработки и восприятия графического изображения алгоритмов их составление осуществляется в соответст­вии с требованиями ГОСТ 19701—90 «Схемы алгоритмов, программ, данных и систем. Условные обозначения и правила выполнения» и ГОСТ 19.003—80 «Схемы алгоритмов и программ. Обозначения ус­ловно- графические».

Изображение схем алгоритмов осуществляется по определенным правилам. В соответствии с этими правилами каждая схема должна начинаться и кончаться соответствующими символами, обозначающими начало и окончание алгоритма.

Все блоки в схеме располагаются в последовательности сверху вниз и слева направо, объединяясь между собой линиями потока. В этом случае направление линий потока не идентифицируется с помощью стрелок, в отличие от других направлений.

С целью повышения наглядности графические схемы алгоритмов могут сопровождаться кратким формально-словесным описанием внутри условного изображения блоков, раскрывающим содержание выполняемой операции. Для обозначения условной передачи управ­ления от блоков логических операций над соответствующими линия­ми потока могут записываться специальные знаки операций отноше­ния (<, >, = и другие) или слова «Да» либо «Нет».

Не нашли, что искали? Воспользуйтесь поиском по сайту: