|
|
Аксиомы теории вероятности.1. Вероятность любого события больше либо равна нулю. 2. Вероятность достоверного события равна единице. 3. Если события А и В несовместны, то вероятность их суммы равна сумме их вероятностей. Следствия
Дифференциальное исчисление функции одной переменной Рассмотрим некоторую функцию у =f(х), заданную в интервале (а, b), и точку x, принадлежащую ему. Зададим в этой точке приращение ∆х, такое, что х+∆х
Производной функции f(x) в точке х называют предел отношения приращения функции ∆f(x) к приращению аргумента ∆х, когда ∆х стремится к нулю:
Рассмотрим геометрический смысл производной. Пусть дана некоторая функция f(х). Значение производной этой функции в точке х0 равно угловому коэффициенту (касательной, проведенной к графику функции через точку (х0, y0), где y0=f(x0): Уравнение касательной, проведенной к графику функции y=f(x) в точке М(х0, у0), в общем виде записывается следующим образом: Физический смысл производной заключается в следующем: пусть зависимость пути, пройденного материальной точкой, от времени описывается функцией s =f(t). Производная этой функции в точке t0 равна значению мгновенной скорости движения материальной точки в данный момент времени:
Экономический смыслпроизводной рассмотрим на примере производственной функции. Производственной называют функцию, устанавливающую зависимость объема выпускаемой продукции Q от величины затрат х: Q =f(x). Производная данной функции показывает, насколько изменится объем выпуска продукции при увеличении затрат на единицу, т.е. эффективность затрат. Таким образом, производная характеризует эффективность определенного экономического фактора. Перечислим правила дифференцирования:
Производная сложной функции вида y = f(g(x)) равна y' = f'(g(x))g'(x). Приведем таблицу производных основных элементарных функций: 1. (kx + b)' = k' 2. (хn)'= пхn-1; 3. (х2)'=2х; 4. 5. sin'x = cosx; 6. cos'x = -sinx; Дифференциалом функции у = f(x) называют главную линейную относительно ∆х часть приращения ∆у. Дифференциал функции обозначают dy или df(x). Как следует из определения, dy = А∆х. Для выяснения геометрического смысла дифференциала рассмотрим график функции у(х). Приращение функции ∆у = у1 - у0 можно представить в виде у = АС=АВ + ВС. Найдем катет ВС ∆МВС: ВС = MС · tga = (х1 - x0) tgα = ∆xy'. Тогда ∆у = у'∆х + АВ. Отсюда следует, что приращение у состоит из двух частей, причем главная линейно зависимая относительно ∆х часть приращения имеет вид у'∆х, т.е. dy = y'∆x. Для функции у = х последняя формула примет вид dx = x'∆x, а так как х' = 1, имеем dx = ∆x.C учетом этого факта выражение для дифференциала функции примет вид dy = y'dx.
При достаточно малых приращениях ∆y = dy. Это соотношение можно использовать для приближенных вычислений качений функции. Учитывая, что ∆у = у-у0 и dx = ∆х, получаем формулу для приближенных вычислений: у = у0 + у'∆х. Производной второго порядка или второй производной у" называют производную от первой производной: у" = (y')'. Разрыв функции. С понятием предела функции тесно связано другое важное понятие математического анализа — понятие непрерывности функции. Рассмотрим функцию f(x), определенную на некотором промежутке. Пусть х0 — некоторая точка этого промежутка, в которой функция имеет значение f(x0). В определении предела функции f(х) при х, стремящемся к x0, отмечалось, что число х0 может и не принадлежать области определения функции f(x), а если число х0 и принадлежит области определения, значение функции в этой точке при изучении предела нас не интересовало. Однако большой интерес представляет именно случай, когда
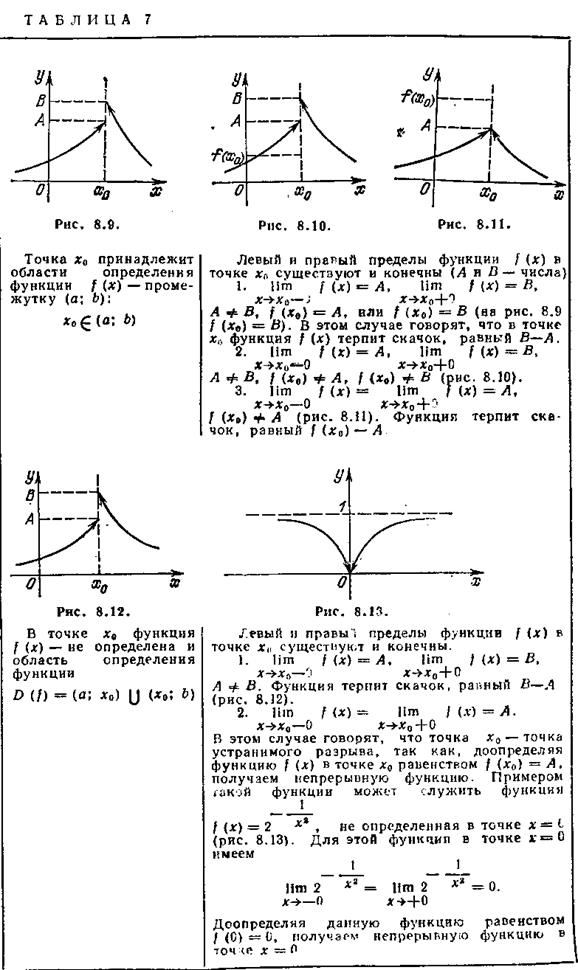
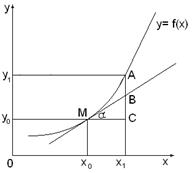
Говорят, что функция / (х) непрерывна в точке х0, если выполняется равенство (1); если же равенство (I) не выполняется, то говорят, что в точке х0 функция терпит разрыв. Таким образом, выяснение вопроса о непрерывности функции f(х) в какой-либо точке х0, принадлежащей области определения функции, сводится к вычислению предела функции в точке х0 и проверке справедливости равенства (1). Если функция f(х) определена на промежутке (а, b) и непрерывна в каждой точке промежутка, то говоря, что функция непрерывнана этом промежутке. Основные теоремы о непрерывных функциях.Непрерывность элементарных функций. 1) Если функции f (х) и g (х) определены на промежутке (а,b) и непрерывны в точке х0
также непрерывны (последняя функция непрерывна при условии, что g (x0) ≠ 0). 2) Если функция у=f (х) непрерывна в точке x0, а функция g(y) непрерывна в точке у0 = f (х0), то и сложная функция g (f(х)) непрерывна в точке х0.
Теорема Больцано—Коши находит весьма неожиданное применение при решении алгебраических уравнений, а именно, она позволяет доказать, что любое алгебраическое уравнение нечетной степени с действительными коэффициентами
имеет по крайней мере один действительный корень.
(2)
(3)
Если равенство (2) не выполнятся, то говорят, что функция f(х) разрывна в точке х0 слева, если не выполняется равенство (3), то функция разрывна в точке х0 справа. Если функция f (x) определена на промежутке (а; b) и точка х0 Различают следующие виды разрывов функции в точке: разрывы первого рода и разрывы второго рода.
Функция. График. Применение методов дифференциального исчислении позволяет проанализировать поведение функции на всей области ее определения. Для проведения такого анализа необходимо дать определения критической точки, экстремума функции, точки перегиба и др. Точка x0, принадлежащая области определения функции f(x) называется точкой максимума (минимума),если существует такое δ > 0, что для любого х ≠ х0 из интервала (х0 - δ, х0 + δ) выполняется неравенство f(х)<f(х0) (f(x) <f(х0)). Точки минимума и максимума называют точками экстремума функции. Необходимое условие экстремумазаключается в следующем: если точка x0 является точкой экстремума функции f(х) и в этой точке существует f'(.х), то f'(x) = 0. Точки, в которых f'(x) = 0, называют критическими точками 1-го рода. Не все критические точки являются точками экстремума. Рассмотрим достаточные условия экстремума: 1) имеется некоторая функция f(х), непрерывная в точке x0, для которой в окрестности точки x0 (х0 -δ, х0 + δ), где δ > 0, быть может за исключением самой точки x0, существует производная f'(x). Если эта производная при переходе через точку х0: а) меняет знак с « + » на « - », то точка х0 является точкой максимума; б) меняет знак с « - » на « + », то точка х0 является точкой минимума; в) не меняет знак, то точка x0 не является точкой экстремума; 2) имеется некоторая функция f(x), для которой в окрестности точки х0 (х0 -δ, х0 + δ), где δ > 0, существуют первая и вторая производные, причем f'(xQ) = 0, a f"(x0) ≠0. Тогда: а) при f"(x0) < 0 функция имеет максимум; б) при f"(xо) > 0 функция имеет минимум. Приведем признаки возрастания и убывания функции. Пусть имеется некоторая дифференцируемая функция f(х). Она будет возрастать (убывать) в некотором интервале (а,b), если ее производная f'(xо) имеет положительный (отрицательный) знак в любой точке этого интервала. Рассмотрим понятие выпуклости функции. График функции называется выпуклым вверхв интервале (а, b), если он расположен ниже касательной, проведенной к нему в любой точке интервала (a, b). Если график функции лежит выше касательной, проведенной в любой точке рассматриваемого интервала, то он называется выпуклым внизв этом интервале Если функция f(х) имеет первую и вторую производные в интервале (а, b) и f"(x) > 0, то график функции имеет в этом интервале выпуклость вниз, и наоборот, при f"(х) < 0 график функции обращен выпуклостью вверх. Точка графика функции f(х), в которой функция непрерывна и существует касательная, называется точкой перегиба, если при переходе через нее график меняет направление выпуклости. Пусть функция f(х) непрерывна и имеет непрерывные первую и вторую производные в интервале (а, b). Тогда в точке перегиба х0 Точки, в которых f"(x) = 0, называют критическими точками 2-го рода. Приведем общую схему исследования функции. 1. Найти область определения функции и, если это возможно, определить по виду функции множество ее значений. 2. Определить точки разрыва функции. 3. Найти точки пересечения графика функции с осью абсцисс (у = 0) и осью ординат (х = 0), а также интервалы знакопостоянства функции. 4. Исследовать функцию на четность и нечетность, а так же на периодичность. 5. Найти критические точки 1-го рода. I 6. Определить интервалы возрастания и убывания функции, найти ее экстремумы. 7. Найти критические точки 2-го рода. 8. Определить интервалы выпуклости и найти точки перегиба. 9. Найти асимптоты. 10. Построить график функции. Линейная функция Линейной функцией называется функция вида f (x) =kх + b, где k и b— некоторые числа. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 (а, b). В этом случае функция получает приращение ∆f(x) = f(x +∆x) – f(x).
(а, b). В этом случае функция получает приращение ∆f(x) = f(x +∆x) – f(x).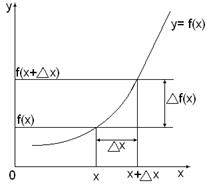
 .
.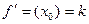
 .
. .
. .
. ;
;
 (1)
(1)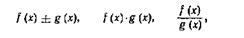
 3) Первая теорема Больцано — Коши. Если функция f(х) задана на промежутке [а;b] и непрерывна в промежутке (a; b) и если на концах промежутка значения функции f (а) и f (b) имеют разные знаки, то между а и b существует (по крайней мере одно) такое значение х0, прикотором f(х) обращается в нуль:
3) Первая теорема Больцано — Коши. Если функция f(х) задана на промежутке [а;b] и непрерывна в промежутке (a; b) и если на концах промежутка значения функции f (а) и f (b) имеют разные знаки, то между а и b существует (по крайней мере одно) такое значение х0, прикотором f(х) обращается в нуль: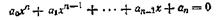
 4) Первая теорема Beйерштрасса. Если функция f (х) определена и непрерывна на промежутке [а, b], то она ограничена па этом промежутке, т. е. существуют такие два числа т и М, что для всех х
4) Первая теорема Beйерштрасса. Если функция f (х) определена и непрерывна на промежутке [а, b], то она ограничена па этом промежутке, т. е. существуют такие два числа т и М, что для всех х  Односторонняя непрерывность.Классификация разрывов функций. Пусть функция f (x) определена на промежутке (а; x0]. Говорят, что функция f (x) непрерывна в точке x0 слева, если
Односторонняя непрерывность.Классификация разрывов функций. Пусть функция f (x) определена на промежутке (а; x0]. Говорят, что функция f (x) непрерывна в точке x0 слева, если Аналогично, функция f (х), определенная на промежутке [х0; b), непрерывна в точке x0 справа, если
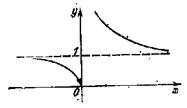
Аналогично, функция f (х), определенная на промежутке [х0; b), непрерывна в точке x0 справа, если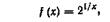 Перечень разрывов первого рода приведен в табл, 7, Если хотя бы один из односторонних пределов в точке x0 не существует или равен +∞ (—∞), то говорят, что функция f(х) имеет в точке х0 разрыв второго рода (точка х0 может как принадлежать, так и не принадлежать области определения функции). Примером функции, имеющей разрыв второго рода, может служить функция
Перечень разрывов первого рода приведен в табл, 7, Если хотя бы один из односторонних пределов в точке x0 не существует или равен +∞ (—∞), то говорят, что функция f(х) имеет в точке х0 разрыв второго рода (точка х0 может как принадлежать, так и не принадлежать области определения функции). Примером функции, имеющей разрыв второго рода, может служить функция